NEET-XII-Physics
32: Electric Current in Conductors
- #21Consider N = n1n2 identical cells, each of emf ε and internal resistance r. Suppose n1 cells are joined in series to form a line and n2 such lines are connected in parallel.
The combination drives a current in an external resistance R. (a) Find the current in the external resistance. (b) Assuming that n1 and n2 can be continuously varied, find the relation between n1, n2, R and r for which the current in R is maximum. (a) Find the current in the external resistance. (b) Assuming that n1 and n2 can be continuously varied, find the relation between n1, n2, R and r for which the current in R is maximum.Ans : (a)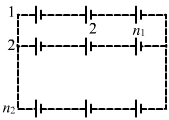
Given:
Emf of one cell = E
∴ Total e.m.f. of n1 cells in one row = n1E
Total emf of one row will be equal to the net emf across all the n2 rows because of parallel connection.
Total resistance in one row = n1r
Total resistance of n2 rows in parallel `` =\frac{{n}_{1}r}{{n}_{2}}``
Net resistance of the circuit = R + `` \frac{{n}_{1}r}{{n}_{2}}``
`` \therefore \,\mathrm{\,Current\,},I=\frac{{n}_{1}E}{R+{\displaystyle \frac{{n}_{1}r}{{n}_{2}}}}=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}`` (b) From
(a),
`` I=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}``
For I to be maximum, (n1r + n2R) should be minimum
`` \Rightarrow {\left(\sqrt{{n}_{1}r}-\sqrt{{n}_{2}\,\mathrm{\,R\,}}\right)}^{2}+2\sqrt{{n}_{1}\,\mathrm{\,R\,}{n}_{2}r}=\,\mathrm{\,min\,}``
It is minimum when
`` \sqrt{{n}_{1}r}=\sqrt{{n}_{2}\,\mathrm{\,R\,}}``
`` {n}_{1}r={n}_{2}\,\mathrm{\,R\,}``
∴ I is maximum when n1r = n2R .
Page No 199: (a)
Given:
Emf of one cell = E
∴ Total e.m.f. of n1 cells in one row = n1E
Total emf of one row will be equal to the net emf across all the n2 rows because of parallel connection.
Total resistance in one row = n1r
Total resistance of n2 rows in parallel `` =\frac{{n}_{1}r}{{n}_{2}}``
Net resistance of the circuit = R + `` \frac{{n}_{1}r}{{n}_{2}}``
`` \therefore \,\mathrm{\,Current\,},I=\frac{{n}_{1}E}{R+{\displaystyle \frac{{n}_{1}r}{{n}_{2}}}}=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}`` (b) From
(a),
`` I=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}``
For I to be maximum, (n1r + n2R) should be minimum
`` \Rightarrow {\left(\sqrt{{n}_{1}r}-\sqrt{{n}_{2}\,\mathrm{\,R\,}}\right)}^{2}+2\sqrt{{n}_{1}\,\mathrm{\,R\,}{n}_{2}r}=\,\mathrm{\,min\,}``
It is minimum when
`` \sqrt{{n}_{1}r}=\sqrt{{n}_{2}\,\mathrm{\,R\,}}``
`` {n}_{1}r={n}_{2}\,\mathrm{\,R\,}``
∴ I is maximum when n1r = n2R .
Page No 199:
- #21-aFind the current in the external resistance.Ans :

Given:
Emf of one cell = E
∴ Total e.m.f. of n1 cells in one row = n1E
Total emf of one row will be equal to the net emf across all the n2 rows because of parallel connection.
Total resistance in one row = n1r
Total resistance of n2 rows in parallel `` =\frac{{n}_{1}r}{{n}_{2}}``
Net resistance of the circuit = R + `` \frac{{n}_{1}r}{{n}_{2}}``
`` \therefore \,\mathrm{\,Current\,},I=\frac{{n}_{1}E}{R+{\displaystyle \frac{{n}_{1}r}{{n}_{2}}}}=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}``
- #21-bAssuming that n1 and n2 can be continuously varied, find the relation between n1, n2, R and r for which the current in R is maximum.Ans : From
(a),
`` I=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}``
For I to be maximum, (n1r + n2R) should be minimum
`` \Rightarrow {\left(\sqrt{{n}_{1}r}-\sqrt{{n}_{2}\,\mathrm{\,R\,}}\right)}^{2}+2\sqrt{{n}_{1}\,\mathrm{\,R\,}{n}_{2}r}=\,\mathrm{\,min\,}``
It is minimum when
`` \sqrt{{n}_{1}r}=\sqrt{{n}_{2}\,\mathrm{\,R\,}}``
`` {n}_{1}r={n}_{2}\,\mathrm{\,R\,}``
∴ I is maximum when n1r = n2R .
Page No 199: