Qstnid -Iv-15-take The Potential Of The Point B In Figure (31-e7) To Be Zero. (A) Find The Potentials At The Points C And D. (B) If A Capacitor Is Connected Between C And D, What Charge Will Appear On This Capacitor? figure (A) Find The Potentials At The Points C And D. (B) If A Capacitor Is Connected Between C And D, What Charge Will Appear On This Capacitor? figure - 31: Capacitors

Home Learn Fast select Course

Show Unit/Chapter Change Unit Change Subject Last Menu

NEET-XII-Physics

31: Capacitors

with Solutions - page 4

Qstn# iv-15 Prvs-Qstn Next-Qstn

#15
Take the potential of the point B in figure (31-E7) to be zero. (a) Find the potentials at the points C and D. (b) If a capacitor is connected between C and D, what charge will appear on this capacitor?
Figure (a) Find the potentials at the points C and D. (b) If a capacitor is connected between C and D, what charge will appear on this capacitor?
Figure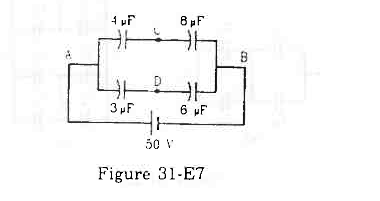
Ans :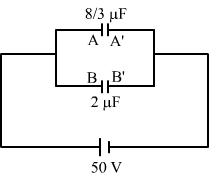 (a) The capacitance of the two rows connected in parallel is given by
`` {C}_{1}=\frac{4\times 8}{4+8}=\frac{8}{3}\,\mathrm{\,\mu F\,}`` and `` {C}_{2}=\frac{3\times 6}{3+6}=\frac{18}{9}\,\mathrm{\,\mu F\,}=2\,\mathrm{\,\mu F\,}``
As the two rows are in parallel, the potential difference across each row is the same and is equal to 50 V.
The charge on the branch ACB with capacitance `` \frac{8}{3}\,\mathrm{\,\mu F\,}`` is given by
Q = `` \left(\frac{8}{3}\,\mathrm{\,\mu F\,}\right)``×(50 V) = `` \frac{400}{3}\,\mathrm{\,\mu C\,}``
The charge on the branch ADB with capacitance `` 2\,\mathrm{\,\mu F\,}`` is given by
`` Q=C\times V``
`` Q=2\,\mathrm{\,\mu F\,}\times 50=100\,\mathrm{\,\mu C\,}``
The potential at point D is given by
`` {V}_{\,\mathrm{\,D\,}}=\frac{q}{{\,\mathrm{\,C\,}}_{1}}=\frac{100\,\mathrm{\,\mu C\,}}{6\,\mathrm{\,\mu F\,}}``
`` {V}_{\,\mathrm{\,D\,}}=\frac{50}{3}\,\mathrm{\,V\,}``
Similarly, the potential at point C is given by
`` {V}_{\,\mathrm{\,C\,}}=\frac{50}{3}\,\mathrm{\,V\,}`` (b) As the potential difference between points C and D is zero, the bridge remains balanced and no charge flows from C to D. If a capacitor is connected between points C and D, then the change on the capacitor will be zero.
Page No 166: (a) The capacitance of the two rows connected in parallel is given by
`` {C}_{1}=\frac{4\times 8}{4+8}=\frac{8}{3}\,\mathrm{\,\mu F\,}`` and `` {C}_{2}=\frac{3\times 6}{3+6}=\frac{18}{9}\,\mathrm{\,\mu F\,}=2\,\mathrm{\,\mu F\,}``
As the two rows are in parallel, the potential difference across each row is the same and is equal to 50 V.
The charge on the branch ACB with capacitance `` \frac{8}{3}\,\mathrm{\,\mu F\,}`` is given by
Q = `` \left(\frac{8}{3}\,\mathrm{\,\mu F\,}\right)``×(50 V) = `` \frac{400}{3}\,\mathrm{\,\mu C\,}``
The charge on the branch ADB with capacitance `` 2\,\mathrm{\,\mu F\,}`` is given by
`` Q=C\times V``
`` Q=2\,\mathrm{\,\mu F\,}\times 50=100\,\mathrm{\,\mu C\,}``
The potential at point D is given by
`` {V}_{\,\mathrm{\,D\,}}=\frac{q}{{\,\mathrm{\,C\,}}_{1}}=\frac{100\,\mathrm{\,\mu C\,}}{6\,\mathrm{\,\mu F\,}}``
`` {V}_{\,\mathrm{\,D\,}}=\frac{50}{3}\,\mathrm{\,V\,}``
Similarly, the potential at point C is given by
`` {V}_{\,\mathrm{\,C\,}}=\frac{50}{3}\,\mathrm{\,V\,}`` (b) As the potential difference between points C and D is zero, the bridge remains balanced and no charge flows from C to D. If a capacitor is connected between points C and D, then the change on the capacitor will be zero.
Page No 166:

#15-a
Find the potentials at the points C and D.
Ans : The capacitance of the two rows connected in parallel is given by
`` {C}_{1}=\frac{4\times 8}{4+8}=\frac{8}{3}\,\mathrm{\,\mu F\,}`` and `` {C}_{2}=\frac{3\times 6}{3+6}=\frac{18}{9}\,\mathrm{\,\mu F\,}=2\,\mathrm{\,\mu F\,}``
As the two rows are in parallel, the potential difference across each row is the same and is equal to 50 V.
The charge on the branch ACB with capacitance `` \frac{8}{3}\,\mathrm{\,\mu F\,}`` is given by
Q = `` \left(\frac{8}{3}\,\mathrm{\,\mu F\,}\right)``×(50 V) = `` \frac{400}{3}\,\mathrm{\,\mu C\,}``
The charge on the branch ADB with capacitance `` 2\,\mathrm{\,\mu F\,}`` is given by
`` Q=C\times V``
`` Q=2\,\mathrm{\,\mu F\,}\times 50=100\,\mathrm{\,\mu C\,}``
The potential at point D is given by
`` {V}_{\,\mathrm{\,D\,}}=\frac{q}{{\,\mathrm{\,C\,}}_{1}}=\frac{100\,\mathrm{\,\mu C\,}}{6\,\mathrm{\,\mu F\,}}``
`` {V}_{\,\mathrm{\,D\,}}=\frac{50}{3}\,\mathrm{\,V\,}``
Similarly, the potential at point C is given by
`` {V}_{\,\mathrm{\,C\,}}=\frac{50}{3}\,\mathrm{\,V\,}``

#15-b
If a capacitor is connected between C and D, what charge will appear on this capacitor?
Figure
Ans : As the potential difference between points C and D is zero, the bridge remains balanced and no charge flows from C to D. If a capacitor is connected between points C and D, then the change on the capacitor will be zero.
Page No 166: