NEET-XII-Physics
28: Heat Transfer
- #28-aCalculate the rate of heat flow through the closed window when the temperature inside the room is 32°C and the outside is 40°C. (b) The glass is now replaced by two glasspanes, each having a thickness of 1 mm and separated by a distance of 1 mm. Calculate the rate of heat flow under the same conditions of temperature. Thermal conductivity of window glass = 1.0 J s-1 m-1°C-1 and that of air = 0.025 J s-1 m-1°C-1.Ans :
Length, l = 2 mm = 0.0002 m
`` \,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,flow\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}=\frac{∆T}{l/KA}``
`` =\frac{KA.∆T}{l}``
`` =\frac{1\times 2\times \left(40-32\right)}{2\times {10}^{-3}}``
`` =8000\,\mathrm{\,J\,}/\,\mathrm{\,sec\,}`` (b)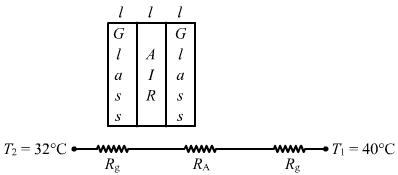
Resistance of glass, `` {R}_{\,\mathrm{\,g\,}}=\frac{l}{{K}_{\,\mathrm{\,g\,}}.A}``
Resistance of air, `` {R}_{\,\mathrm{\,A\,}}=\frac{l}{{K}_{\,\mathrm{\,A\,}}.A}``
From the circuit diagram, we can find that all the resistors are connected in series.
`` {R}_{s}={R}_{g}+{R}_{A}+{R}_{g}``
`` =\frac{{10}^{-3}}{2}\left(\frac{2}{{K}_{\,\mathrm{\,g\,}}}+\frac{1}{{K}_{\,\mathrm{\,A\,}}}\right)``
`` =\frac{{10}^{-3}}{2}\left(\frac{2}{1}+\frac{1}{0.025}\right)``
`` =\frac{{10}^{-3}}{2}\times \frac{\left(2\times 0.025+1\right)}{0.025}``
`` ``
`` \,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,flow\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,},q=\frac{∆T}{{R}_{s}}``
`` =\frac{{T}_{1}-{T}_{2}}{{R}_{s}}``
`` =\frac{\left(40-32\right)\times 2\times 0.025}{{40}^{-3}\times \left(2\times 0.025+1\right)}``
`` =381W``
Page No 100:
- #28-bThe glass is now replaced by two glasspanes, each having a thickness of 1 mm and separated by a distance of 1 mm. Calculate the rate of heat flow under the same conditions of temperature. Thermal conductivity of window glass = 1.0 J s-1 m-1°C-1 and that of air = 0.025 J s-1 m-1°C-1.Ans :

Resistance of glass, `` {R}_{\,\mathrm{\,g\,}}=\frac{l}{{K}_{\,\mathrm{\,g\,}}.A}``
Resistance of air, `` {R}_{\,\mathrm{\,A\,}}=\frac{l}{{K}_{\,\mathrm{\,A\,}}.A}``
From the circuit diagram, we can find that all the resistors are connected in series.
`` {R}_{s}={R}_{g}+{R}_{A}+{R}_{g}``
`` =\frac{{10}^{-3}}{2}\left(\frac{2}{{K}_{\,\mathrm{\,g\,}}}+\frac{1}{{K}_{\,\mathrm{\,A\,}}}\right)``
`` =\frac{{10}^{-3}}{2}\left(\frac{2}{1}+\frac{1}{0.025}\right)``
`` =\frac{{10}^{-3}}{2}\times \frac{\left(2\times 0.025+1\right)}{0.025}``
`` ``
`` \,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,flow\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,},q=\frac{∆T}{{R}_{s}}``
`` =\frac{{T}_{1}-{T}_{2}}{{R}_{s}}``
`` =\frac{\left(40-32\right)\times 2\times 0.025}{{40}^{-3}\times \left(2\times 0.025+1\right)}``
`` =381W``
Page No 100: