23: Heat And Temperature : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

23: Heat and Temperature

with Solutions - page 2

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#
Section : ii

Qstn #1
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
(a) must be in thermal equilibrium
(b) cannot be in thermal equilibrium
(c) may be in thermal equilibrium
digAnsr: c
Ans : (c) may be in thermal equilibrium
The given data in the question is insufficient to specify the relation between the physical conditions of systems Y and Z. As system X is not in thermal equilibrium with Y and Z, systems Y and Z may be at the same temperature or they may or may not be in thermal equilibrium with each other. So, the only possible option is
(c).
Page No 11:

Qstn #2
Which of the curves in the figure (23-Q1) represents the relation between Celsius and Fahrenheit temperatures?
Faigure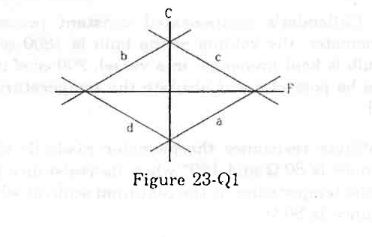
Ans : (a)
Celsius and Fahrenheit temperatures are related in the following way:
`` C=\frac{5}{9}F-\frac{160}{9}``
Here, F = temperature in Fahrenheit
C = temperature in Celsius
If this equation is plotted on the graph, then the curve will be represented by curve 'a' lying in the fourth quadrant with slope 5/9.
So, the correct option is
(a).
Page No 11:

Qstn #3
Which of the following pairs may give equal numerical values of the temperature of a body?
(a) Fahrenheit and Kelvin
(b) Celsius and Kelvin
(c) Kelvin and Platinum
digAnsr: a
Ans : (a) Fahrenheit and Kelvin
Let θ be the temperature in Fahrenheit and Kelvin scales.
We know that the relation between the temperature in Fahrenheit and Kelvin scales is given by
`` \frac{{T}_{\,\mathrm{\,F\,}}-32}{180}=\frac{{T}_{\,\mathrm{\,K\,}}-273.15}{100}``
T_F = T_K = θ
Therefore,
`` \frac{\theta -32}{180}=\frac{\theta -273.15}{100}``
`` 5\theta -160=9\theta -2458.5``
`` 4\theta =2298.35``
`` \theta =574.59{}^{\,\mathrm{\,o\,}}``
If we consider the same for Celsius and Kelvin scales
`` \frac{{T}_{\,\mathrm{\,C\,}}-0}{100}=\frac{{T}_{\,\mathrm{\,K\,}}-273.15}{100}``
Let the temperature be t
`` \frac{t-0}{100}=\frac{t-273.15}{100}``
`` t=t-273.15``
Thus, t does not exist.
The Kelvin scale uses mercury as thermometric substance, whereas the platinum scale uses platinum as thermometric substance. The scale depends on the properties of the thermometric substance used to define the scale. The platinum and Kelvin scales do not agree with each other. Therefore, there is no such temperature that has same numerical value in the platinum and Kelvin scale.
Page No 11:

Qstn #4
For a constant-volume gas thermometer, one should fill the gas at
(a) low temperature and low pressure
(b) low temperature and high pressure
(c) high temperature and low pressure
(d) high temperature and high pressure
digAnsr: c
Ans : (c) high temperature and low pressure.
A constant-volume gas thermometer should be filled with an ideal gas in which particles don't interact with each other and are free to move anywhere, so that the thermometer functions properly. An ideal gas is only a theoretical possibility. Therefore, the gas that is filled in the thermometer should be at high temperature and low pressure, as under these conditions, a gas behaves as an ideal gas.
Page No 11:

Qstn #5
Consider the following statements.
(A) The coefficient of linear expansion has dimension K^-1.
(B) The coefficient of volume expansion has dimension K^-1.

(a) A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) A and B are wrong.
digAnsr: a
Ans : (a) A and B are correct.
The coefficient of linear expansion,
`` \alpha =\frac{1}{L}\frac{\&traingle;L}{\&traingle;T}``
`` ``
`` =\frac{\left[L\right]}{\left[LT\right]}={\,\mathrm{\,K\,}}^{-1}``
Here, L = initial length
`` \&traingle;``L = change in length
`` \&traingle;``T = change in temperature
On the other hand, the coefficient of volume expansion,
`` \gamma =\frac{1}{V}\frac{\&traingle;V}{\&traingle;T}=\frac{\left[{L}^{3}\right]}{\left[{L}^{3}T\right]}={\,\mathrm{\,K\,}}^{-1}``
Here, V = initial volume
`` \&traingle;``V = change in volume
`` \&traingle;``T = change in temperature
K = kelvin, the S.I. unit of temperature
Page No 12:

Qstn #6
A metal sheet with a circular hole is heated. The hole
(a) gets larger
(b) gets smaller
(c) retains its size
(d) is deformed
digAnsr: a
Ans : (a) gets larger
When a metal sheet is heated, it starts expanding and its surface area will start increasing, which will lead to an increase in the radius of the hole. Hence, the circular hole will become larger.
Page No 12:

Qstn #7
Two identical rectangular strips, one of copper and the other of steel, are riveted together to form a bimetallic strip (α_copper > α_steel). On heating, this strip will
(a) remain straight
(b) bend with copper on convex side
(c) bend with steel on convex side
(d) get twisted
digAnsr: b
Ans : (b) bend with copper on convex side
We are provided with two metal strips of copper and steel. On heating, both of them will expand. Expansion coefficient of copper is more than that of steel. So, the copper metal strip will expand more, causing the bimetallic strip to bend with copper at the convex side, as it'll have more surface area compared to the steel sheet, which will be on the concave side.
Page No 12:

Qstn #8
If the temperature of a uniform rod is slightly increased by &traingle;t, its moment of inertia I about a perpendicular bisector increases by
(a) zero
(b) αI&traingle;t
(c) 2αI&traingle;t
(d) 3αI&traingle;t.
digAnsr: c
Ans : (c) 2αI∆t
The change in moment of inertia of uniform rod with change in temperature is given by,
`` I\text{'}=I(1+2\alpha \Delta t)``
Here, I = initial moment of inertia
I' = new moment of inertia due to change in temperature
`` \alpha ``= expansion coefficient
`` ∆``t = change in temperature
So, `` I\text{'}-I=2\alpha I\Delta t``
Page No 12:

Qstn #9
If the temperature of a uniform rod is slightly increased by &traingle;t, its moment of inertia I about a line parallel to itself will increase by
(a) zero
(b) αI&traingle;t
(c) 2αI&traingle;t
(d) 3αI&traingle;t.
digAnsr: c
Ans :
(c) 2αI∆t
The moment of inertia of a solid body of any shape changes with temperature as
`` I\text{'}=I\left(1+2\alpha \Delta t\right)``
Here, I = initial moment of inertia
I' = new moment of inertia due to change in temperature
`` \alpha `` = expansion coefficient
`` \Delta ``t = change in temperature
So, `` I\text{'}-I=2\alpha I\Delta t``
Page No 12:

Qstn #10
The temperature of water at the surface of a deep lake is 2°C. The temperature expected at the bottom is
(a) 0 °C
(b) 2 °C
(c) 4 °C
(d) 6 °C
digAnsr: c
Ans : (c) 4^oC
The density of water is maximum at 4^oC, and the water at the bottom of the lake is most dense, compared to the layers of water above. Therefore, the temperature expected at the bottom is 4^oC.
Page No 12:

Qstn #11
An aluminium sphere is dipped into water at 10°C. If the temperature is increased, the force of buoyancy
(a) will increase
(b) will decrease
(c) will remain constant
(d) may increase or decrease depending on the radius of the sphere
digAnsr: b
Ans : (b) will decrease
When an aluminium sphere is dipped in water and the temperature of water is increased, the aluminium will start expanding leading to increase in its volume. This will lead to increase in the surface area of the shell and it'll exert less pressure on the water such that the volume of the sphere submerged in water will decrease and it'll start float easily on water. Now, the volume of water displaced will be less compared to what was displaced initially. Therefore, the force of buoyancy will decrease, as it is directly proportional to the volume of water displaced.
Page No 12:

#
Section : iii

Qstn #1
A spinning wheel is brought in contact with an identical wheel spinning at identical speed. The wheels slow down under the action of friction. Which of the following energies of the first wheel decreases?
(a) Kinetic
(b) Total
(c) Mechanical
(d) Internal
digAnsr: a,c
Ans : (a) Kinetic
(c) Mechanical
The kinetic energy of a body depends on its speed. Since when a spinning wheel is slowed down, its speed decreases leading to reduction in its kinetic energy. The mechanical energy of a body is defined as the sum of its potential and kinetic energies. Since the kinetic energy of the wheel has been decreased, it'll lead to decrease in its mechanical energy. When the wheel slows down due to friction, its mechanical energy gets converted into heat energy, leading to increase in internal energy, which increases with increase in temperature.
Page No 12:

Qstn #2
A spinning wheel A is brought in contact with another wheel B, initially at rest. Because of the friction at contact, the second wheel also starts spinning. Which of the following energies of the wheel B increases?
(a) Kinetic
(b) Total
(c) Mechanical
(d) Internal
digAnsr: a,b,c,d
Ans : (a) Kinetic
(b) Total
(c) Mechanical
(d) Internal
When the wheel B starts spinning because of the friction at contact, it will gain kinetic energy and, hence, mechanical energy (kinetic + potential energies). Also, internal energy will increase, which increases with rise in temperature. Along with it, the generation of heat energy due to friction will lead to increase in the net sum of all the energies, i.e. total energy.
Page No 12: