NEET-XII-Physics
03: Current Electricity
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #18-cA low voltage supply from which one needs high currents must have very low internal resistance. Why?Ans : According to Ohm’s law, the relation for the potential is V = IR
Voltage (V) is directly proportional to current (I).
R is the internal resistance of the source.
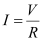
If V is low, then R must be very low, so that high current can be drawn from the source.
- #18-dA high tension (HT) supply of, say, 6 kV must have a very large internal resistance. Why?Ans : In order to prohibit the current from exceeding the safety limit, a high tension supply must have a very large internal resistance. If the internal resistance is not large, then the current drawn can exceed the safety limits in case of a short circuit.
- #19-aAlloys of metals usually have (greater/less) resistivity than that of their constituent metals.Ans : Alloys of metals usually have greater resistivity than that of their constituent metals.
- #19-bAlloys usually have much (lower/higher) temperature coefficients of resistance than pure metals.Ans : Alloys usually have lower temperature coefficients of resistance than pure metals.
- #19-cThe resistivity of the alloy manganin is nearly independent of/increases rapidly with increase of temperature.Ans : The resistivity of the alloy, manganin, is nearly independent of increase of temperature.
- #19-dThe resistivity of a typical insulator (e.g., amber) is greater than that of a metal by a factor of the order of (1022/103).Ans : The resistivity of a typical insulator is greater than that of a metal by a factor of the order of 1022.
- #20
- #20-aGiven n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?Ans : Total number of resistors = n
Resistance of each resistor = R
(i) When n resistors are connected in series, effective resistance R1is the maximum, given by the product nR.
Hence, maximum resistance of the combination, R1 = nR
(ii) When n resistors are connected in parallel, the effective resistance (R2) is the minimum, given by the ratio .
.
Hence, minimum resistance of the combination, R2 =
(iii) The ratio of the maximum to the minimum resistance is,

- #20-bGiven the resistances of 1 ``\Omega``, 2 ``\Omega``, 3 ``\Omega``, how will be combine them to get an equivalent resistance of (i) (11/3) ``\Omega`` (ii) (11/5) ``\Omega``, (iii) 6 ``\Omega``, (iv) (6/11) ``\Omega``?Ans : The resistance of the given resistors is,
R1 = 1 ``\Omega``, R2 = 2 ``\Omega``, R3 = 3 ``\Omega``2
- Equivalent resistance,
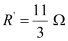
Consider the following combination of the resistors.

Equivalent resistance of the circuit is given by,
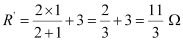
- Equivalent resistance,
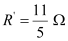
Consider the following combination of the resistors.
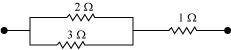
Equivalent resistance of the circuit is given by,
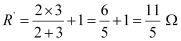
(iii) Equivalent resistance, R’ = 6 ``\Omega``
Consider the series combination of the resistors, as shown in the given circuit.
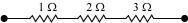
Equivalent resistance of the circuit is given by the sum,
R’ = 1 + 2 + 3 = 6 ``\Omega``
(iv) Equivalent resistance,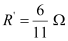
Consider the series combination of the resistors, as shown in the given circuit.
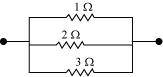
Equivalent resistance of the circuit is given by,
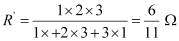
- Equivalent resistance,
- #20-cDetermine the equivalent resistance of networks shown in Fig. 3.31.
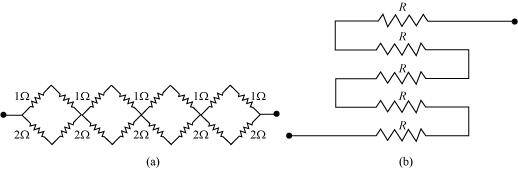
Ans : (a) It can be observed from the given circuit that in the first small loop, two resistors of resistance 1 ``\Omega`` each are connected in series.
Hence, their equivalent resistance = (1+1) = 2 ``\Omega``
It can also be observed that two resistors of resistance 2 ``\Omega`` each are connected in series.
Hence, their equivalent resistance = (2 + 2) = 4 ``\Omega``.
Therefore, the circuit can be redrawn as

It can be observed that 2 ``\Omega`` and 4 ``\Omega`` resistors are connected in parallel in all the four loops. Hence, equivalent resistance (R’) of each loop is given by,
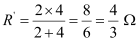
The circuit reduces to,

All the four resistors are connected in series.
Hence, equivalent resistance of the given circuit is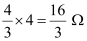
(b) It can be observed from the given circuit that five resistors of resistance R each are connected in series.
Hence, equivalent resistance of the circuit = R + R + R + R + R
= 5 R
2
- Qstn #21Determine the current drawn from a 12 V supply with internal resistance 0.5 ``\Omega`` by the infinite network shown in Fig. 3.32. Each resistor has 1 ``\Omega`` resistance.
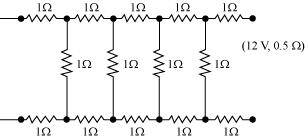
Ans : The resistance of each resistor connected in the given circuit, R = 1 ``\Omega``
Equivalent resistance of the given circuit = R’
The network is infinite. Hence, equivalent resistance is given by the relation,
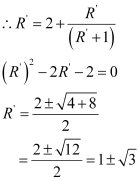
Negative value of R’ cannot be accepted. Hence, equivalent resistance,
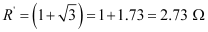
Internal resistance of the circuit, r = 0.5 ``\Omega``
Hence, total resistance of the given circuit = 2.73 + 0.5 = 3.23 ``\Omega``
Supply voltage, V = 12 V
According to Ohm’s Law, current drawn from the source is given by the ratio,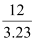 = 3.72 A
= 3.72 A
- Qstn #22Figure 3.33 shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 ``\Omega`` maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for very moderate currents up to a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of 600 k``\Omega`` is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found similarly, turns out to be at 82.3 cm length of the wire.
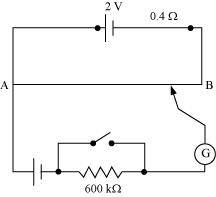
- #22-aWhat is the value ε ?Ans : Constant emf of the given standard cell, E1 = 1.02 V
Balance point on the wire, l1 = 67.3 cm
A cell of unknown emf, ε,replaced the standard cell. Therefore, new balance point on the wire, l = 82.3 cm
The relation connecting emf and balance point is,
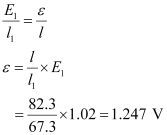 The value of unknown emfis 1.247 V.
The value of unknown emfis 1.247 V.
- #22-bWhat purpose does the high resistance of 600 k``\Omega`` have?Ans : The purpose of using the high resistance of 600 k``\Omega`` is to reduce the current through the galvanometer when the movable contact is far from the balance point.