NEET-XII-Physics
02: Electrostatic Potential And Capacitance
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #15-bIs the electric field inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape? Explain.Ans : Yes
The electric field intensity inside a cavity is zero, even if the shell is not spherical and has any irregular shape. Take a closed loop such that a part of it is inside the cavity along a field line while the rest is inside the conductor. Net work done by the field in carrying a test charge over a closed loop is zero because the field inside the conductor is zero. Hence, electric field is zero, whatever is the shape.
- #16
- #16-aShow that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
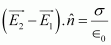
Where
is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of is from side 1 to side 2.) Hence show that just outside a conductor, the electric field is σ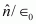 
Ans : Electric field on one side of a charged body is E1 and electric field on the other side of the same body is E2. If infinite plane charged body has a uniform thickness, then electric field due to one surface of the charged body is given by,
Where,
= Unit vector normal to the surface at a point
σ = Surface charge density at that point
Electric field due to the other surface of the charged body,
Electric field at any point due to the two surfaces,
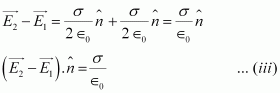
Since inside a closed conductor,
= 0,
∴
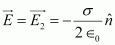
Therefore, the electric field just outside the conductor is
.
- #16-bShow that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]Ans : When a charged particle is moved from one point to the other on a closed loop, the work done by the electrostatic field is zero. Hence, the tangential component of electrostatic field is continuous from one side of a charged surface to the other.
- Qstn #17A long charged cylinder of linear charged density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?
Ans : Charge density of the long charged cylinder of length L and radius r is λ.
Another cylinder of same length surrounds the pervious cylinder. The radius of this cylinder is R.
Let E be the electric field produced in the space between the two cylinders.
Electric flux through the Gaussian surface is given by Gauss’s theorem as,
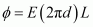
Where, d = Distance of a point from the common axis of the cylinders
Let q be the total charge on the cylinder.
It can be written as
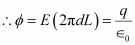
Where,
q = Charge on the inner sphere of the outer cylinder
∈0 = Permittivity of free space
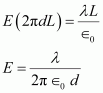
Therefore, the electric field in the space between the two cylinders is
.
- Qstn #18In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Ã…:
Ans : The distance between electron-proton of a hydrogen atom,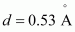
Charge on an electron, q1 = -1.6 ×10-19 C
Charge on a proton, q2 = +1.6 ×10-19 C
- #18-aEstimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.Ans : Potential at infinity is zero.
Potential energy of the system, = Potential energy at infinity - Potential energy at distance d
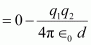
where,
∈0 is the permittivity of free space
14``\pi``ε0=9×109Nm2C-2∴Potentialenergy=0-9×109×1.6×10-1920.53×10-10=-43.47×10-19J∵1.6×10-19J=1eV∴Potentialenergy=-43.7×10-19=-43.7×10-191.6×10-19=-27.2eV
Therefore, the potential energy of the system is -27.2 eV.
- #18-bWhat is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?Ans : Kinetic energy is half of the magnitude of potential energy.
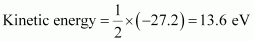
Total energy = 13.6 - 27.2 = 13.6 eV
Therefore, the minimum work required to free the electron is 13.6 eV.
- #18-cWhat are the answers to (a) and (b) above if the zero of potential energy is taken at 1.06 Ã… separation?Ans : When zero of potential energy is taken,
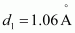
∴Potential energy of the system = Potential energy at d1 - Potential energy at d
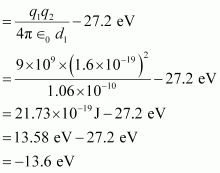
Page No 89:
- Qstn #19If one of the two electrons of a H2 molecule is removed, we get a hydrogen molecular ion
. In the ground state of an, the two protons are separated by roughly 1.5 Ã…, and the electron is roughly 1 Ã… from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
Ans : The system of two protons and one electron is represented in the given figure.
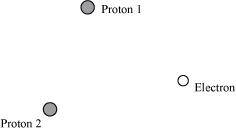
Charge on proton 1, q1 = 1.6 ×10-19 C
Charge on proton 2, q2 = 1.6 ×10-19 C
Charge on electron, q3 = -1.6 ×10-19 C
Distance between protons 1 and 2, d1 = 1.5 ×10-10 m
Distance between proton 1 and electron, d2 = 1 ×10-10 m
Distance between proton 2 and electron, d3 = 1 × 10-10 m
The potential energy at infinity is zero.
Potential energy of the system,
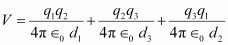
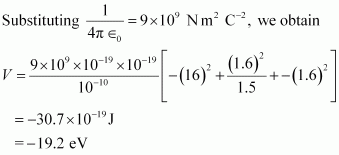
Therefore, the potential energy of the system is -19.2 eV.
- Qstn #20Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
Ans : Let a be the radius of a sphere A, QA be the charge on the sphere, and CA be the capacitance of the sphere. Let b be the radius of a sphere B, QB be the charge on the sphere, and CB be the capacitance of the sphere. Since the two spheres are connected with a wire, their potential (V) will become equal.
Let EAbe the electric field of sphere A and EB be the electric field of sphere B. Therefore, their ratio,
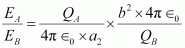
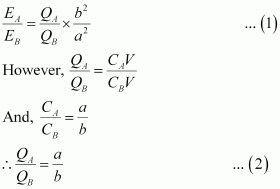
Putting the value of (2) in (1), we obtain
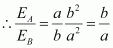
Therefore, the ratio of electric fields at the surface is
.
A sharp and pointed end can be treated as a sphere of very small radius and a flat portion behaves as a sphere of much larger radius.Therefore, charge density on sharp and pointed ends of the conductor is much higher than on its flatter portions.
- #21-aWhat is the electrostatic potential at the points?Ans : Zero at both the points
Charge - q is located at (0, 0, - a) and charge + q is located at (0, 0, a). Hence, they form a dipole. Point (0, 0, z) is on the axis of this dipole and point (x, y, 0) is normal to the axis of the dipole. Hence, electrostatic potential at point (x, y, 0) is zero. Electrostatic potential at point (0, 0, z) is given by,
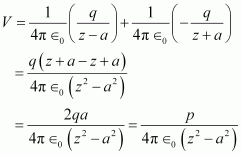
Where,
.gif)
= Permittivity of free space
p = Dipole moment of the system of two charges = 2qa
- #21-bObtain the dependence of potential on the distance r of a point from the origin when r/a >> 1.Ans : Distance r is much greater than half of the distance between the two charges. Hence, the potential (V) at a distance r is inversely proportional to square of the distance i.e.,
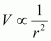
- #21-cHow much work is done in moving a small test charge from the point (5, 0, 0) to (-7, 0, 0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?Ans : Zero
The answer does not change if the path of the test is not along the x-axis.
A test charge is moved from point (5, 0, 0) to point (-7, 0, 0) along the x-axis. Electrostatic potential (V1) at point (5, 0, 0) is given by,
V1=-q4``\pi``∈01(5-0)2+(-a)2+q4``\pi``∈01(5-0)2+(a)2=-q4``\pi``∈025+a2+q4``\pi``∈025+a2=0Electrostatic potential, V2, at point (- 7, 0, 0) is given by,
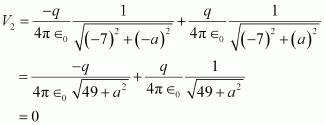
Hence, no work is done in moving a small test charge from point (5, 0, 0) to point (-7, 0, 0) along the x-axis.
The answer does not change because work done by the electrostatic field in moving a test charge between the two points is independent of the path connecting the two points.