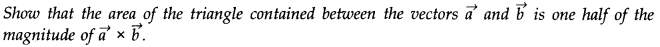NEET-XI-Physics
07: System of particles and Rotational Motion
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #
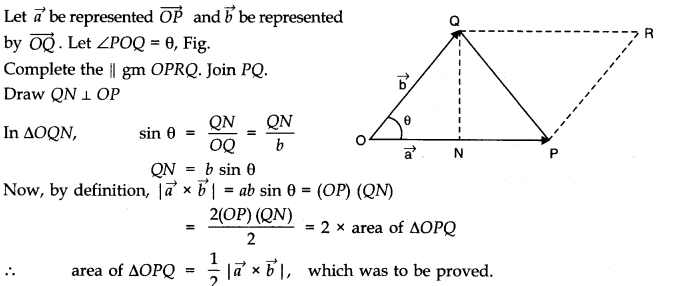
- Qstn #1Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?Ans : In all the four cases, as the mass density is uniform, centre of mass is located at their respective geometrical centres.
No, it is not necessary that the centre of mass of a body should lie on the body. For example, in case of a circular ring, centre of mass is at the centre of the ring, where there is no mass.
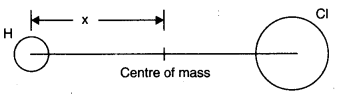
- Qstn #2In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 A (1 A = 10-10m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.Ans : Let us choose the nucleus of the hydrogen atom as the origin for measuring distance. Mass of hydrogen atom,m1= 1 unit (say) Since cholorine atom is 35.5 times as massive as hydrogen atom,
.•. mass of cholorine atom, m2 = 35.5 units
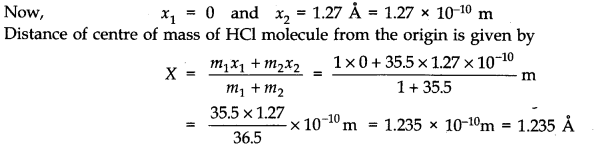
- Qstn #3A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?Ans : When the child gets up and runs about on the trolley, the speed of the centre of mass of the trolley and child remains unchanged irrespective of the manner of motion of child. It is because here child and trolley constitute one single system and forces involved are purely internal forces. As there is no external force, there is no change in momentum of the system and velocity remains unchanged.
- Qstn #6Find the components along the x, y, z-axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and pz. Show that if the particle moves only in the x-y plane the angular momentum has only a z- component.Ans :

- Qstn #7Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system the same whatever be the point about which the angular momentum is taken.Ans :
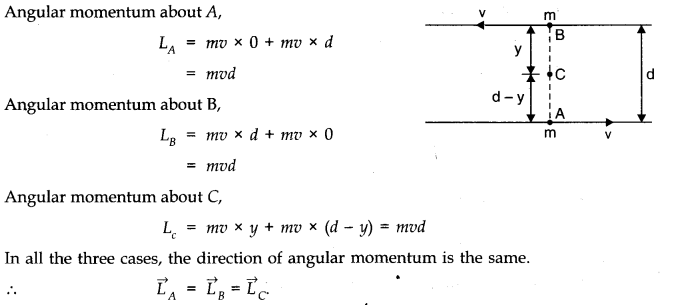
- Qstn #8A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9° and ‘ 53.2° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
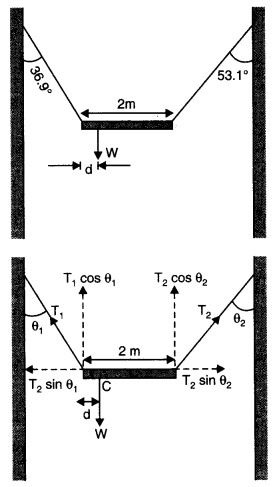
Ans :
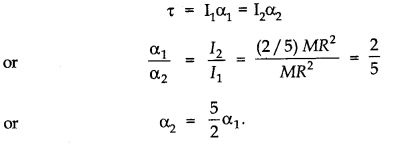
- Qstn #9A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.Ans : Let F1 and F2 be the forces exerted by the level groundon front wheels and back wheels respectively.Considering rotational equilibrium about the front wheels,F2 x 1.8 = mg x 1.05or F2 = 1.05/1.8 x 1800 x 9.8 N =10290 NForce on each back wheel is =10290/2 N or 5145 N.
Considering rotational equilibrium about the back wheels.
F1 x 1.8 = mg (1.8 - 1.05) = 0.75 x 1800 x 9.8
or F1=0.75 x 1800 x 9.8/1.8 = 7350 N
Force on each front wheel is 7350/2 N or 3675 N.
- #10
- #10-aFind the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2 MR2/5, where M is the mass of the sphere and R is the radius of the sphere.Ans : Moment of inertia of sphere about any diameter = 2/5 MR
2
Applying theorem of parallel axes,Moment of inertia of sphere about a tangent to the sphere = 2/5 MR2 +M(R)2 =7/5 MR2
- #10-bGiven the moment of inertia of a disc of mass M and radius R about any of its diameters to 1 be 1/4 MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge.Ans : We are given, moment of inertia of the disc about any of its diameters = 1/4 MR2
(-i) Using theorem of perpendicular axes, moment of inertia of the disc about an axis passing through its centre and normal to the disc = 2 x 1/4 MR2 = 1/2 MR2.
(ii) Using theorem axes, moment of inertia of the disc passing through a point on its edge and normal to the dies = 1/2 MR2+ MR2 = 3/2 MR2.
- Qstn #11Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?Ans : Let M be the mass and R the radius of the hollow cylinder, and also of the solid sphere. Their moments of inertia about the respective axes are I1 = MR2 and I2 = 2/5 MR2
Let τbe the magnitude of the torque applied to the cylinder and the sphere, producing angular accelerations α1andα2 respectively. Thenτ=I1 α1 = I2 α2
The angular acceleration 04 produced in the sphere is larger. Hence, the sphere will acquire larger angular speed after a given time.
- Qstn #12A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s-1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?Ans : M = 20 kg
Angular speed, w = 100 rad s-1; R = 0.25 m
Moment of inertia of the cylinder about its axis
=1/2 MR2 = 1/2 x 20 (0.25)2 kg m2 = 0.625 kg m2
Rotational kinetic energy,
Er = 1/2 Iw2 = 1/2 x 0.625 x (100)2 J = 3125 J
Angular momentum,
L = Iw = 0.625 x 100 Js= 62.5 Js.