39: Alternating Current : Cbse-xi-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

CBSE-XI-Physics

39: Alternating Current

with Solutions -

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#
Section : i

Qstn #1
What is the reactance of a capacitor connected to a constant DC source?
Ans : The reactance of a capacitor is given by,
`` {X}_{c}=\frac{1}{\omega C}``
For a DC source, ω = 0
`` \Rightarrow {X}_{c}=\frac{1}{0\times C}=\infty ``
So, for a constant DC source, reactance of a capacitor is infinite.
Page No 328:

Qstn #2
The voltage and current in a series AC circuit are given by V = V₀cos ωt and i = i₀ sin ωt. What is the power dissipated in the circuit?
Ans : Voltage, V = V₀cos ωt
Current, i = i₀ sin ωt or i = i₀ cos (ωt `` -`` `` \frac{\pi }{2}``)
Power dissipated in an AC circuit is given by,
`` P={I}_{rms}{V}_{rms}\,\mathrm{\,cos\,}\varphi ``,
where I_rms = rms value of current
V_rms= rms value of voltage
ϕ = phase difference between current and voltage
Here, ϕ = `` \pi ``/2
`` \Rightarrow \,\mathrm{\,cos\,}\varphi =\,\mathrm{\,cos\,}\frac{\,\mathrm{\,\pi \,}}{2}=0``
`` \therefore P={I}_{rms}{V}_{rms}\times 0=0``
Page No 328:

Qstn #3
Two alternating currents are given by
i1=i0 sin ωt and i2=i0 sin ωt+π3Will the rms values of the currents be equal or different?
Ans : The rms value of current is given by,
`` {i}_{rms}=\frac{{i}_{0}}{\sqrt{2}}``
Since peak value of current i₀ is same for both currents, their rms values will be same.
Page No 328:

Qstn #4
Can the peak voltage across the inductor be greater than the peak voltage of the source in an LCR circuit?
Ans : Let a LCR circuit is connected across an AC supply with the emf E = E₀ sin ωt.
Let the inductance in the circuit be L
Let the net impedence of the circuit be `` Z=\sqrt{{R}^{2}+({X}_{\,\mathrm{\,L\,}}-{X}_{\,\mathrm{\,C\,}}{)}^{2}}``
Where,
R = resistance in the circuit
X_L= reactance due to inductor
X_C= reactance due to capacitor
The magnitude of the voltage across the inductor is given by
`` V=L\frac{\,\mathrm{\,d\,}i}{\,\mathrm{\,d\,}t}``
The current in the circuit can be written as `` I={I}_{0}\,\mathrm{\,sin\,}(\omega t+\varphi )``
Where, ϕ is the phase difference between the current and the supply voltage
Thus, the voltage across the inductor can be written as
`` V=L{I}_{0}\,\mathrm{\,cos\,}(\omega t+\varphi )``
Thus peak value of the voltage across the inductor is given by
`` V=L{I}_{0}``
`` \Rightarrow V=\frac{{E}_{0}}{Z}\times L``
Therefore, the peak voltage across the inductor is given by `` V=\frac{{E}_{0}}{Z}\times L``
At resonance Z = R,
`` V=\frac{{E}_{0}}{R}\times L``,
If `` \frac{L}{R}>1``
V > E₀
Therefore if magnitude of `` \frac{L}{R}>1`` at resonance the value of the voltage across the inductor will bw greater than the peak value of the supply voltage.
Page No 328:

Qstn #5
In a circuit, containing a capacitor and an AC source, the current is zero at the instant the source voltage is maximum. Is it consistent with Ohm’s Law?
Ans : Ohm's Law is valid for resistive circuits only. It is not valid for capacitive or inductive circuits, or a combination of both.
Page No 328:

Qstn #6
An AC source is connected to a capacitor. Will the rms current increase, decrease or remain constant if a dielectric slab is inserted into the capacitor?
Ans : The reactance of a capacitor is given by,
`` {X}_{c}=\frac{1}{\omega C}``
Also,
`` C=\frac{K{\epsilon }_{0}A}{d}``,
where C = capacitance
K = dielectric constant
A = area of plates
d = distance between the plates.
`` K>1``
`` \therefore `` The capacitance C of the capacitor will increase on inserting the dielectric slab and, consequently, the reactance X_c will decrease.
Rms current, `` {i}_{rms}=\frac{{\epsilon }_{0}}{\sqrt{2}{X}_{C}}``
Therefore, rms current will decrease.
Page No 328:

Qstn #7
When the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero. Does it mean that there is no current through the inductor or the capacitor?
Ans : The condition for resonance is:
`` \frac{1}{\omega C}=\omega L``
The peak current through the circuit is given by,
`` {i}_{0}=\frac{{V}_{0}}{{\sqrt{{R}^{2}+\left({\displaystyle \frac{1}{\omega C}}-\omega L\right)}}^{2}}``
`` ``
From the condition of resonance, we get:
`` {i}_{0}=\frac{{V}_{0}}{R}``
The current will flow through the all circuit elements. But since the reactance of the capacitor and inductor are equal, the potential difference across them will be equal and opposite and will cancel each other.
Page No 328:

Qstn #8
When an AC source is connected to a capacitor, there is a steady-state current in the circuit. Does it mean that the charges jump from one plate to the other to complete the circuit?
Ans : No. When an AC source is connected to a capacitor, there is a steady in the circuit to transfer change to the plates of the capacitor. This produces a potential difference between the plates. The capacitance is alternatively charged and discharged as the current reverses after each half cycle.
Page No 329:

Qstn #9
A current i₁ = i₀ sin ωt passes through a resistor of resistance R. How much thermal energy is produced in one time period? A current i₂ = -i₀ sin ωt passes through the resistor. How much thermal energy is produced in one time period? If i₁ and i₂ both pass through the resistor simultaneously, how much thermal energy is produced? Is the principle of superposition obeyed in this case?
Ans : The thermal energy produced for an AC circuit in one time period is given by,
`` H={{I}_{rms}}^{2}\times R\times \frac{2\,\mathrm{\,\pi \,}}{\omega }``
For current, i₁ = i₀ sin ωt,
`` {I}_{rms}=\frac{{i}_{0}}{\sqrt{2}}``
`` \Rightarrow H=\frac{{{i}_{0}}^{2}R}{2}\times \frac{2\,\mathrm{\,\pi \,}}{\omega }=\frac{\,\mathrm{\,\pi \,}{{i}_{0}}^{2}R}{\omega }``
For current, i₂ = -i₀ sin ωt,
`` {I}_{rms}=\frac{{i}_{0}}{\sqrt{2}}``
Hence, the same thermal energy will be produced due to this current.
Since, the direction of i₁ and i₂ are opposite and their magnitude is same, the net current through the resistor will become zero when both are passed together. Yes, the principle of superposition is obeyed in this case.
Page No 329:

Qstn #10
Is energy produced when a transformer steps up the voltage?
Ans : When a transformer steps up the voltage, the voltage increases but current decreases. Neglecting any loss of energy, the power remains constant and, hence, energy is not produced. It remains constant.
Page No 329:

Qstn #11
A transformer is designed to convert an AC voltage of 220 V to an AC voltage of 12 V. If the input terminals are connected to a DC voltage of 220 V, the transformer usually burns. Explain.
Ans : A transformer is ideally an inductive coil. For an inductor connected across a DC voltage,

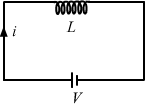
`` V-L\frac{di}{dt}=0``
`` \Rightarrow V=L\frac{di}{dt}``
`` \Rightarrow \int di=\frac{V}{L}\int dt``
`` \Rightarrow i=\frac{Vt}{L}``
For a DC source, the current across the inductor will increase with time and can reach a very large value, which can burn the transformer.
Page No 329:

Qstn #12
Can you have an AC series circuit in which there is a phase difference of (a) 180° (b) 120° between the emf and the current?
Ans : Let us consider an AC series LCR circuit of angular frequency ω. The impedance of the circuit is given by,
`` Z=\sqrt{{R}^{2}+{\left(\omega L-\frac{1}{\omega C}\right)}^{2}}``
The phase difference between V and I is given by,
`` \,\mathrm{\,tan\,}\varphi =\left(\frac{\omega L-{\displaystyle \frac{1}{\omega C}}}{Z}\right)``
From the above formula, we can clearly see that
`` \varphi \in \left(-\frac{\,\mathrm{\,\pi \,}}{2},\frac{\,\mathrm{\,\pi \,}}{2}\right)``
So, we cannot have a phase difference of 180° or 120°.
Page No 329:

Qstn #13
A resistance is connected to an AC source. If a capacitor is included in the series circuit, will the average power absorbed by the resistance increase or decrease? If an inductor of small inductance is also included in the series circuit, will the average power absorbed increase or decrease further?
Ans : When a capacitor is included in a series circuit, the impedance of the circuit,
`` Z=\sqrt{{R}^{2}+{{X}_{C}}^{2}}``
`` ``
The power absorbed by a resistor is given by,
`` P={{I}_{rms}}^{2}R``
Since impedance increases due to introduction of a capacitor, the rms value of current I_rms will decrease and, hence, the power absorbed by the resistor will decrease.
When a small inductance is introduced in the circuit, the impedance of the circuit,
`` Z=\sqrt{{R}^{2}+{\left({X}_{C}-{X}_{L}\right)}^{2}}``
Since the impedance now decreases a little, the rms value of current will increase and, hence, the power absorbed by the resistor will increase.
Page No 329: