CBSE-XI-Physics
36: Permanent Magnets
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #Section : i
- Qstn #1Can we have a single north pole, or a single south pole?Ans : No, we cannot have a single north or south pole. Magnetic poles are always found in pairs. They are equal in strength and opposite in nature. Even if we break a magnet into a number of pieces, each piece will become a magnet with equal and opposite poles.
Page No 275:
- Qstn #2Do two distinct poles actually exist at two nearby points in a magnetic dipole?Ans : No, two distinct poles cannot exist at two nearby points in a magnet, as a magnet contains only two distinct poles located at its ends.
Page No 275:
- Qstn #3An iron needle is attracted to the ends of a bar magnet but not to the middle region of the magnet. Is the material making up the ends of a bare magnet different from that of the middle region?Ans : No, the material making up the middle region of a magnet is the same as that of the material making up its end. When an iron needle is taken closer to one of the ends of a magnet, the pole of the magnet induces a pole of opposite polarity on the needle, making the needle a magnet itself and thereby making it attracted to that pole.
But if we bring the needle closer to the centre of the magnet, then both the poles of the magnet will induce opposite polarity on the needle. As a result, the needle will not get attracted towards the centre of the magnet.
Page No 275:
- Qstn #4Compare the direction of the magnetic field inside a solenoid with that of the field there if the solenoid is replaced by its equivalent combination of north pole and south pole.Ans : The direction of the magnetic field is the same in both cases, that is, inside a solenoid and inside a bar magnet. In a solenoid, magnetic field lines are directed from one end to the other internally and externally, so they are in the equivalent combination of north and south poles (as shown in figure).
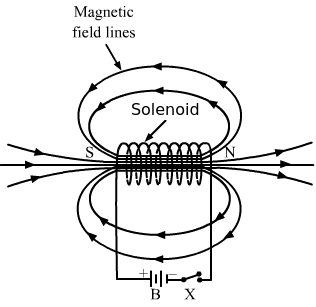
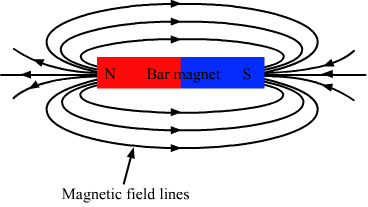
Page No 275:
- Qstn #5Sketch the magnetic field lines for a current-carrying circular loop near its centre. Replace the loop by an equivalent magnetic dipole and sketch the magnetic field lines near the centre of the dipole. Identify the difference.Ans : The difference between the two configurations is that in the current-carrying loop, the magnetic field lines pass through the centre and are perpendicular to its axis; whereas in the equivalent magnetic dipole, the magnetic field lines do not pass through the centre.
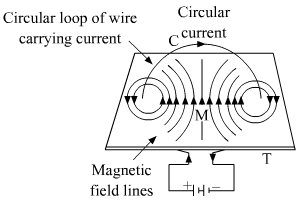
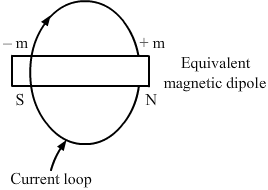
Page No 275:
- Qstn #6The force on a north pole,
F→=mB→, parallel to the field
B→. Does it contradict our earlier knowledge that a magnetic field can exert forces only perpendicular to itself?Ans : Yes, it seems to contradict with our earlier knowledge that a magnetic field can exert forces only perpendicular to itself.
`` \stackrel{\to }{F}=m\stackrel{\to }{B}``
Here,
`` \stackrel{\to }{B}`` = Magnetic field
m = Magnetic charge
For a positive magnetic charge, force is along the magnetic field.
For a negative magnetic charge, force is opposite to the magnetic field.
Thus, it contradicts the notion that a magnetic field can exert forces only perpendicular to itself.
Page No 275:
- Qstn #7Two bar magnets are placed close to each other with their opposite poles facing each other. In absence of other forces, the magnets are pulled towards each other and their kinetic energy increases. Does it contradict our earlier knowledge that magnetic forces cannot do any work and hence cannot increase kinetic energy of a system?Ans : Yes, it contradicts our earlier knowledge that magnetic forces cannot do any work and hence cannot increase the kinetic energy of the system. When opposite poles are facing each other, an attractive force acts between them so the magnets are pulled towards each other. As the two magnets come close to each other so the force between them increases and hence, the kinetic energy also increases.
Page No 275:
- Qstn #8Magnetic scalar potential is defined as
Ur→2-Ur→1=-∫r→1r→2B→.dl→Apply this equation to a closed curve enclosing a long straight wire. The RHS of the above equation is then -μ0 i by Ampere’s law. We see that
Ur→2≠Ur→1even when
r→2=r→1. Can we have a magnetic scalar potential in this case?Ans : No, we cannot have a magnetic scalar potential here.
Ampere's law is a method of calculating magnetic field due to current distribution. On the other hand, magnetic scalar potential requires a magnetic field due to pole strength m.
Potential at a distance r is given by
`` \frac{{\mu }_{0}m}{4\,\mathrm{\,\pi \,}r}``
As there is no current distribution, no magnetic field due to poles or the pole strength is present. That is why we cannot have a magnetic scalar potential in this case.
Page No 275:
- Qstn #9Can the earth’s magnetic field be vertical at a place? What will happen to a freely suspended magnet at such a place? What is the value of dip here?Ans : Yes, Earth's magnetic field is vertical at the poles. A freely suspended magnet becomes vertical at the poles, with its north pole pointing towards Earth's north pole, which is magnetic south.
The value of the angle of the dip here is 90°.
Page No 276:
- #10-azeroAns : Yes, the dip can be zero at the equator of Earth.
- #10-b90°?Ans : Yes, the dip can be 90° at the poles of Earth.
Page No 276:
- Qstn #11The reduction factor K of a tangent galvanometer is written on the instrument. The manual says that the current is obtained by multiplying this factor to tan θ. The procedure works well at Bhuwaneshwar. Will the procedure work if the instrument is taken to Nepal? If there is same error, can it be corrected by correcting the manual or the instrument will have to be taken back to the factory?Ans : Yes, the procedure will work if the instrument is taken to Nepal, as the current at a place can be calculated by multiplying the reduction factor K with tan `` \theta `` of that place. In our case, we will take the value of tan `` \theta `` of Nepal, as tan `` \theta `` may vary from place to place. tan `` \theta `` at any place is determined from the mathematical formula `` \frac{B}{{B}_{H}}``, where B is the external magnetic field and BH is the horizontal component of Earth's magnetic field. Thus, we need not take the manual or the instrument back to the factory for correction.
Page No 276: