34: Magnetic Field : Cbse-xi-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

CBSE-XI-Physics

34: Magnetic Field

with Solutions -

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#
Section : i

Qstn #1
Suppose a charged particle moves with a velocity v near a wire carrying an electric current. So, a magnetic force acts on it. If the same particle is seen from a frame moving with velocity v in the same direction, the charge will be found to be at rest. Will the magnetic force become zero in this frame? Will the magnetic field become zero in this frame?
Ans : Magnetic force becomes zero as the particle is at rest in this frame of reference and we know that force on a particle,
F = qvBsin(`` \theta ``), where v is the velocity of the particle.
So, when v = 0, F = 0.
Magnetic field on the particles still exists because the current is independent of the frame of reference. For any reason, if the electrons of the wire seem to be at rest in a frame of reference, the protons are still flowing opposite to the frame of reference. Due to this, the current and the magnetic fields still exist.
Page No 229:

Qstn #2
Can a charged particle be accelerated by a magnetic field? Can its speed be increased?
Ans : Yes, a charged particle can be accelerated by a magnetic field. A magnetic field exerts force on the charged particle, which is perpendicular to both the magnetic field and velocity. If initially the charged particle is moving at right angle to the magnetic field, then the resultant trajectory of the particle is circular motion. In circular motion, the magnitude of the velocity remains constant but direction changes continuously. So, the motion is accelerated but speed remains constant.
Page No 229:

Qstn #3
Will a current loop placed in a magnetic field always experience a zero force?
Ans : No, it depend on the magnetic field, i.e. whether the field is a uniform or a non-uniform magnetic field and also on the orientation of the current loop. In case of a uniform magnetic field, the force on the circular loop is zero if the magnetic field is parallel to the plane of the loop and in case of a non-uniform magnetic field, the force may or may not be zero.
Page No 229:

Qstn #4
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
Ans : As the electrons are in motion, there is a magnetic force acting on them individually. But the current through the wire represents the collective motion of all the electrons that are moving or vibrating very randomly; so, overall effect is negligible. Hence there is no net magnetic force on the wire.
Also, `` F=ILB\,\mathrm{\,sin\,}\left(\theta \right)``
So, if the current in the wire is zero, then the force experienced by the wire will also be zero.
Page No 229:

Qstn #5
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
Ans : Let us assume that the magnetic field is uniform and is acting along positive x axis in the cubical region.
Now if we project a charged particle inside this cube along positive y axis then as the direction of velocity and magnetic field is perpendicular to each other so the resultant trajectory of the particle will be a circle.
Page No 229:

Qstn #6
An electron beam projected along the positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that the field is parallel to the z-axis?
Ans :
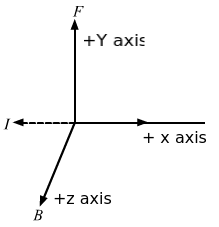
As the particle gets deflected towards the positive y-axis, we can conclude that force is acting on the particle along the positive y-axis. Now, as the electron is moving along the positive x-axis, the current can be assumed to be flowing along the negative x-axis. Applying Fleming's left-hand rule, we find that the thumb points in the direction of force, i.e. the positive y-axis and the middle finger points in the direction of current, i.e. negative x-axis. Consequently, the forefinger gives us the direction of magnetic field, i.e. out of the plane of the paper or in the positive z-direction. So, we can conclude that the magnetic field is pointing along the positive z-axis.
Page No 229:

Qstn #7
Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
Ans : Yes, if the direction of the area vector coincides with the direction of the magnetic field, the torque acting on the loop due to the magnetic field will become zero. Hence, no rotation will be produced in the coil.
It follows from the fact that torque acting on the loop is directly proportional to sin`` \theta ``, where `` \theta `` is the angle made by the area vector with the direction of the magnetic field. So, we can see from this correlation that torque is zero if
`` \theta `` = 0 or `` \theta `` = 180⁰.
`` \tau =\stackrel{\rightharpoonup }{m}\times \stackrel{\rightharpoonup }{B}``
`` =mB\,\mathrm{\,sin\,}\left(\theta \right)``
`` \Rightarrow \,\mathrm{\,For\,}\theta =0\,\mathrm{\,or\,}\,\mathrm{\,integral\,}\,\mathrm{\,multiple\,}\,\mathrm{\,of\,}\,\mathrm{\,\pi \,},``
`` \tau =0``
`` ``
Which implies that the coil will not rotate.
Page No 229:

Qstn #8
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
Ans : The net charge in a current- carrying wire is zero. Yet, negative charge, i.e. electrons are moving in the wire towards the positive terminal. It is this motion of electrons in the conductor which produces the current in the wire and is also responsible for the magnetic force acting on the wire.
F = qVBsin(`` \theta ``), where F is the force, q is the charge of electrons, V is the velocity of electrons and B is the magnetic field.
Moreover, the positive charges on the wire are due to nucleus containing proton. As they are not moving so there is no force on them, so the force is only due to the moving electrons in the wire.
Page No 229:

Qstn #9
The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ = 0 or θ = 180°. In which of the two orientations, the equilibrium is stable?
Ans : If the angle between the positive normal and the magnetic field is 0, then the equilibrium is stable. It follows directly from the fact that U = - mBcos`` \theta ``, where m is the magnetic moment. So, when `` \theta `` is 0, Potential energy, i.e. U of the system is negative, the system is more stable. But if `` \theta `` is `` {180}^{°}``, U is positive or the system is unstable.
Stability of a system depends on its energy and every system tries to minimise its energy. The configuration of the system with least energy is most stable and the configuration with the most energy is least stable or unstable.
Page No 229:

Qstn #10
Verify that the units weber and volt second are the same.
Ans : Force experienced by the charge q moving with velocity v in a magnetic field B is given by
F = qVB
Hence, B = `` \frac{F}{qV}``
Also, weber/m² is the unit for magnetic field B.
Now, equating both the units of the magnetic field B, we get:
`` \frac{Weber}{{m}^{2}}=\frac{F}{q\times V}``
`` \Rightarrow Weber=\frac{F\times {m}^{2}}{q\times m\times {s}^{-1}}=\frac{F\times m}{q\times {s}^{-1}}=\frac{W}{q}\times s=Volt\times s``
Thus, the units weber and volt second are same.
Page No 229:

#
Section : ii

Qstn #1
A positively-charged particle projected towards east is deflected towards north by a magnetic field. The field may be
(a) towards west
(b) towards south
(c) upwards
(d) downwards
digAnsr: d
Ans : (d) downwards
A positively-charged particle projected towards east can be considered as current in the eastern direction. Here, the positive charge is deflected towards the north by a magnetic field, i.e. the positively-charged particle experiences a force in the northern direction.
Hence, in order to determine the direction of the magnetic field, we apply Fleming's left-hand rule. According to this rule, when we stretch the thumb, the fore-finger and the middle finger mutually perpendicular to each other, then the thumb gives the direction of the force experienced by the charged particle, the fore-finger gives the direction of the magnetic field and the middle finger gives the direction of the current. Thus, if we direct the middle finger in the eastern direction, the thumb in the northern direction, we see that the fore-finger points in the downward direction.
Thus, the direction of the magnetic field is found to be in the downward direction.
Page No 229:

Qstn #2
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
(a) will increase
(b) will decrease
(c) will remain the same
(d) may increase or decrease
Ans :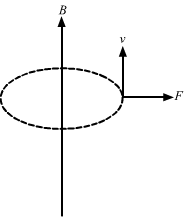
When the charged particle is whirled in a horizontal circle, at any moment, the current direction can be taken along the tangent of the circle. Also, the magnetic field is in the vertical direction. So, using Fleming's left-hand rule, the force can be radially outward or inward, depending on the direction of the magnetic field, i.e. either upward or downward. Also, the direction of force depends on the direction of the whirl, i.e. clockwise or anticlockwise and obviously on the charge of the particle, i.e. whether it is positive or negative. So, the correct answer is that the tension may increase or decrease.
Page No 229: