CBSE-XI-Physics
32: Electric Current in Conductors
- #1Suppose you have three resistors, each of value 30 Ω. List all the different resistances you can obtain using them.Ans : (a) When the three resistors are connected in series:
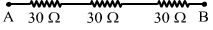
The resultant resistance, Req = R + R + R = 90 `` \Omega ``
(b) When the three resistors are connected in parallel:
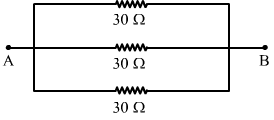
The resultant resistance of the combination,
`` \frac{1}{{R}_{eq}}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}=\frac{3}{R}=\frac{3}{30}=\frac{1}{10}``
`` ``
`` \Rightarrow {R}_{eq}=10\Omega ``
(c) When two of the resistors are connected in parallel and this combination is connected in series with the third resistor:
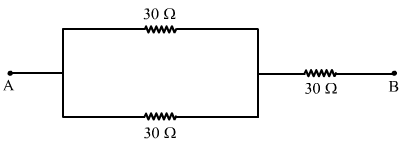
Let R' be the resultant resistance of the two resistors connected in parallel to each other. Therefore,
`` \frac{1}{R\text{'}}=\frac{1}{R}+\frac{1}{R}=\frac{2}{R}=\frac{2}{30}=\frac{1}{15}``
`` \Rightarrow R\text{'}=15\Omega ``
Now, the net resistance of the combination of the resistors,
Req = R' + R = 15 + 30 = 45 `` \Omega ``
(d) When two of the resistors are connected in series and the combination is connected to the third resistor in parallel:
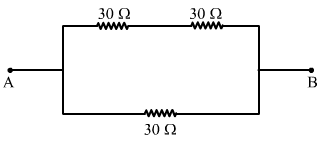
Let R' be the resultant resistance of the series in combination. Therefore,
R' = R + R = 30 + 30 = 60 `` \Omega ``
Now, let the net resultant of the combination be Req. So,
`` \frac{1}{{R}_{eq}}=\frac{1}{R\text{'}}+\frac{1}{R}=\frac{1}{60}+\frac{1}{30}=\frac{3}{60}=\frac{1}{20}``
`` \Rightarrow {R}_{eq}=20\Omega ``
Page No 196: