32: Electric Current In Conductors : Cbse-xi-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

CBSE-XI-Physics

32: Electric Current in Conductors

with Solutions -

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#
Section : i

Qstn #1
Suppose you have three resistors, each of value 30 Ω. List all the different resistances you can obtain using them.
Ans : (a) When the three resistors are connected in series:

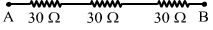
The resultant resistance, R_eq = R + R + R = 90 `` \Omega ``
(b) When the three resistors are connected in parallel:

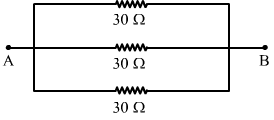
The resultant resistance of the combination,
`` \frac{1}{{R}_{eq}}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}=\frac{3}{R}=\frac{3}{30}=\frac{1}{10}``
`` ``
`` \Rightarrow {R}_{eq}=10\Omega ``
(c) When two of the resistors are connected in parallel and this combination is connected in series with the third resistor:

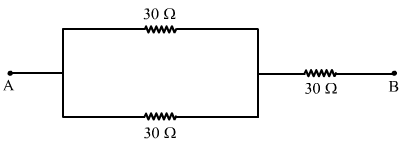
Let R' be the resultant resistance of the two resistors connected in parallel to each other. Therefore,
`` \frac{1}{R\text{'}}=\frac{1}{R}+\frac{1}{R}=\frac{2}{R}=\frac{2}{30}=\frac{1}{15}``
`` \Rightarrow R\text{'}=15\Omega ``
Now, the net resistance of the combination of the resistors,
R_eq = R' + R = 15 + 30 = 45 `` \Omega ``
(d) When two of the resistors are connected in series and the combination is connected to the third resistor in parallel:

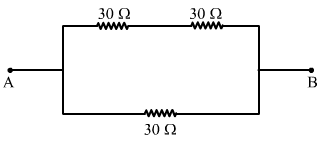
Let R' be the resultant resistance of the series in combination. Therefore,
R' = R + R = 30 + 30 = 60 `` \Omega ``
Now, let the net resultant of the combination be R_eq. So,
`` \frac{1}{{R}_{eq}}=\frac{1}{R\text{'}}+\frac{1}{R}=\frac{1}{60}+\frac{1}{30}=\frac{3}{60}=\frac{1}{20}``
`` \Rightarrow {R}_{eq}=20\Omega ``
Page No 196:

Qstn #2
A proton beam is moving from east to west. Is there an electric current? If yes, in what direction?
Ans : Yes, there is an electric current in the direction of the proton beam. Conventionally, the direction of electric current is same as that of the positive charge flow.
Page No 196:

Qstn #3
In an electrolyte, the positive ions move from left to right and the negative ions from right to left. Is there a net current? If yes, in what direction?
Ans : Yes, there is a net current that flows from left to right. By convention, the direction of current is along the flow of positive charge. As the positive ions move from left to right, current also moves from left to right. Also, since the negative ions move from right to left, current moves from left to right. Thus, the movement of net current is from left to right.
Page No 196:

Qstn #4
In a TV tube, electrons are accelerated from the rear to the front. What is the direction of the current?
Ans : Conventionally, the direction of current is along the direction of flow of positive charge and opposite the direction of flow of negative charge. In a TV tube, current will flow from the front to the rear, as the direction of current is opposite the direction in which electrons are moving.
Page No 196:

Qstn #5
Drift speed is defined as v_d = Δl/Δt, where Δl is the distance drifted in a long time Δt. Why don’t we define drift speed as the limit of Δl/Δt as Δt → 0?
Ans : An electron drifts under the influence of an external electric field. During the course of this motion, an electron follows a very random path. So, we have to take the average for a very long time. Hence, we cannot define drift speed as the limit of Δl/Δt as Δt → 0 because this is a very short interval of time that is not enough to get the desired result.
Page No 196:

Qstn #6
One of your friends says that he has read in the previous chapters that there can be no electric field inside a conductor. Consequently, there can be no current through it. What is the fallacy of this argument?
Ans : You have studied in the previous chapters that when a static charge is given to a metal, the charge resides on its surface and there is no electric field inside it. But this is not the case when a charge is in motion. Current can flow through a conductor only when an electric field is established inside it. An electric field exists inside the conductor, as it is connected to the battery. Thus, current flows through the conductor.
Page No 196:

Qstn #7
When a current is established in a wire, the free electrons drift in the direction opposite to the current. Does the number of free electrons in the wire continuously decrease?
Ans : No, the number of electrons in the wire remains constant. The electrons that drift and move to the positive terminal of the battery, under the influence of the external electric field, are replaced by the battery in the circuit. As a result, the total number of free electrons in the wire is always constant.
Page No 196:

Qstn #8
A fan with copper winding in its motor consumes less power compared to a similar fan with aluminium winding. Explain.
Ans : A copper wire has higher conductance than an aluminium wire. So, a copper wire offer less resistance to the current flow than an aluminium wire. Thus, there is more heat dissipation in an aluminium wire than in a copper wire. This is why a fan with copper winding in its motor consumes less power compared to a similar fan with aluminium winding.
Page No 196:

Qstn #9
The thermal energy developed in a current-carrying resistor is given by U = i² Rt and also by U = Vit. Should we say that U is proportional to i² or i?
Ans : In the expression U = Vit, voltage V and current i are variables for a given time interval. So, based on this expression we cannot say that U is proportional to i. In the expression U = i²Rt, the resistance R is fixed for a circuit for a given time interval. So, based on this expression, we can say that U is proportional to i² and not i.
Page No 196:

Qstn #10
Consider a circuit containing an ideal battery connected to a resistor. Do “work done by the battery” and “the thermal energy developed” represent two names of the same physical quantity?
Ans : Yes, the "work done by the battery" and "the thermal energy developed" represent two names of the same physical quantity. The work done by the battery on the resistor is dissipated by the resistor in the form of thermal energy. Hence the " work done by the battery " and " the thermal energy developed " represent two names of the same physical quantity.
However, a non-ideal battery, in this case, would have to do extra work in order to overcome the internal resistance of the battery. Hence, the work done by a non-ideal battery will not be equal to the thermal energy developed.
Page No 196:

Qstn #11
Is work done by a battery always equal to the thermal energy developed in electrical circuit? What happens if a capacitor is connected in the circuit?
Ans : No, the work done by a battery is not always equal to the thermal energy developed in the electrical circuit. In case of a non-ideal battery, the work done by the battery is the sum of the thermal energy developed in the electric circuit and the thermal energy developed in the internal resistance of the battery. In case of a capacitor, the work done by the battery is equal to C V². An amount of energy equal to `` \frac{1}{2}`` C V² is stored in it when it is fully charged, which is a form of electrical energy and not a form of thermal energy. During the charging of the capacitor, `` \frac{1}{2}`` C V²of energy is lost in the form of heat and electromagnetic radiation.
Page No 196:

Qstn #12
A non-ideal battery is connected to a resistor. Is work done by the battery equal to the thermal energy developed in the resistor? Will your answer change if the battery is ideal?
Ans : No, the work done by a non-ideal battery is not equal to the thermal energy developed in the resistor, as energy is spent to overcome the internal resistance of the battery and the resistance of the wire that connects the circuit elements/resistor to the battery. However, the resistance of the wire is generally negligible.
Yes, the answer will change if the battery is ideal. An ideal battery has no internal resistance. Hence, the work done by an ideal battery will be equal to the thermal energy developed in the resistor, assuming that the resistance of the wires used for connection is negligible.
Page No 196:

Qstn #13
Sometimes it is said that “heat is developed” in a resistance when there is an electric current in it. Recall that heat is defined as the energy being transferred due to temperature difference. Is the statement in quotes technically correct?
Ans : Yes, the given statement is correct. When charge flows through a conductor, its electric potential energy decreases. This loss in electric potential energy appears as increased heat energy of the resistor. Thus, heat energy is developed in a resistor when there is an electric current in it.
Page No 196: