31: Capacitors : Cbse-xi-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

CBSE-XI-Physics

31: Capacitors

with Solutions - page 2

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #6
The energy density in the electric field created by a point charge falls off with the distance from the point charge as
(a)
1r
(b)
1r2
(c)
1r3
(d)
1r4.
digAnsr: d
Ans : (d) `` \frac{1}{{r}^{4}}``
Energy density U is given by
U = `` \frac{1}{2}{\in }_{0}{E}^{2}`` ...(1)
The electric field created by a point charge at a distance r is given by
E = `` \frac{q}{4\,\mathrm{\,\pi \,}{\in }_{0}{r}^{\mathit{2}}}``
On putting the above form of E in eq. 1, we get
U = `` \frac{1}{2}{\in }_{0}{\left(\frac{q}{4\,\mathrm{\,\pi \,}{\in }_{0}{r}^{\mathit{2}}}\right)}^{2}``
Thus, U is directly proportional to `` \frac{1}{{r}^{4}}``.
Page No 164:

Qstn #7
A parallel-plate capacitor has plates of unequal area. The larger plate is connected to the positive terminal of the battery and the smaller plate to its negative terminal. Let Q, and Q be the charges appearing on the positive and negative plates respectively.
(a) Q, > Q
(b) Q, = Q
(c) Q, < Q
(d) The information is not sufficient is decide the relation between Q, and Q.
digAnsr: b
Ans : (b) `` {Q}_{+}={Q}_{-}``
The charge induced on the plates of a capacitor is independent of the area of the plates.
∴ `` {Q}_{+}={Q}_{-}``
Page No 164:

Qstn #8
A thin metal plate P is inserted between the plates of a parallel-plate capacitor of capacitance C in such a way that its edges touch the two plates (figure 31-Q2). The capacitance now becomes
(a) C/2
(b) 2 C
(c) 0
(d) ∞.
Figure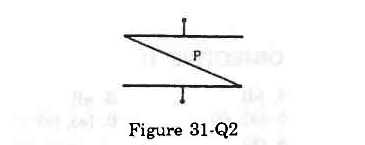
digAnsr: d
Ans : (d) `` \infty ``
The thin metal plate inserted between the plates of a parallel-plate capacitor of capacitance C connects the two plates of the capacitor; hence, the distance d between the plates of the capacitor reduces to zero. It can be observed that the charges on the plates begin to overlap each other via the metallic plate and hence begin to conduct continuously.
Mathematically,
C = `` \frac{{\in }_{0}A}{d}``
In this case, d = 0.
∴ C = `` \infty ``
Page No 164:

Qstn #9
Figure (31-Q3) shows two capacitors connected in series and joined to a battery. The graph shows the variation in potential as one moves from left to right on the branch containing the capacitors.
(a) C₁ > C₂
(b) C₁ = C₂
(c) C₁ < C₂
(d) The information is not sufficient to decide the relation between C₁ and C₂.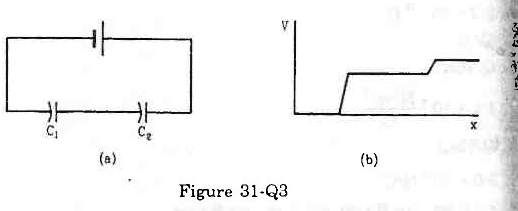
digAnsr: c
Ans : (c) C₁ < C₂

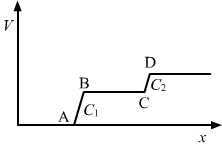
Region AB shows the potential difference across capacitor C₁ and region CD shows the potential difference across capacitor C₂. Now, we can see from the graph that region AB is greater than region CD. Therefore, the potential difference across capacitor C₁ is greater than that across capacitor C₂.
∵ Capacitance, C = `` \frac{Q}{V}``
∴ C₁ < C₂ (Q remains the same in series connection.)
Page No 164:

Qstn #10
Two metal plates having charges Q, -Q face each other at some separation and are dipped into an oil tank. If the oil is pumped out, the electric field between the plates will
(a) increase
(b) decrease
(c) remain the same
(d) become zero.
digAnsr: a
Ans : (a) increase
Oil between the plates of the capacitor acts as a dielectric. We know that the electric field decreases by a factor of `` \frac{1}{K}`` of the original field when we insert a dielectric between the plates of a capacitor (K is the dielectric constant of the dielectric). So, if the oil is pumped out, the electric field between the plates will increase, as the dielectric has been removed.
Page No 164:

Qstn #11
Two metal spheres of capacitance C₁ and C₂ carry some charges. They are put in contact and then separated. The final charges Q₁ and Q₂ on them will satisfy
(a)
Q1Q2<C1C2
(b)
Q1Q2=C1C2
(c)
Q1Q2>C1C2
(d)
Q1Q2=C2C1.
digAnsr: b
Ans : (b) `` \frac{{Q}_{1}}{{Q}_{2}}=\frac{{C}_{1}}{{C}_{2}}``
When the spheres are connected, charges flow between them until they both acquire the same common potential V.
The final charges on the spheres are given by
Q₁= C₁V and Q₂ = C₂V
`` \therefore \frac{{Q}_{1}}{{Q}_{2}}=\frac{{C}_{1}V}{{C}_{2}V}`` = `` \frac{{C}_{1}}{{C}_{2}}``
C1C2V
Page No 164:

Qstn #12
Three capacitors of capacitances 6 µF each are available. The minimum and maximum capacitances, which may be obtained are
(a) 6 µF, 18 µF
(b) 3 µF, 12 µF
(c) 2 µF, 12 µF
(d) 2 µF, 18 µF.
digAnsr: d
Ans :
(d) 2 µF, 18 µF
The minimum capacitance can be obtained by connecting all capacitors in series. It can be calculated as follows:
`` \frac{1}{C}=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}``
`` \Rightarrow ``C = 2 µF
The maximum capacitance can be obtained by connecting all capacitors in parallel. It can be calculated as follows:
C = 6 + 6 + 6 = 18 µF
Page No 164:

#
Section : iii

Qstn #1
The capacitance of a capacitor does not depend on
(a) the shape of the plates
(b) the size of the plates
(c) the charges on the plates
(d) the separation between the plates.
digAnsr: c
Ans : (c) the charges on the plates
The capacitance of a capacitor is given by
C = `` \frac{{\in }_{0}A}{d}``
Here, A is the area of the plates of the capacitor and d is the distance between the plates.
So, we can clearly see that the capacitance of a capacitor does depend on the size and shape of the plates and the separation between the plates; it does not depend on the charges on the plates.

Page No 164:

Qstn #2
A dielectric slab is inserted between the plates of an isolated charged capacitor. Which of the following quantities will remain the same?
(a) The electric field in the capacitor
(b) The charge on the capacitor
(c) The potential difference between the plates
(d) The stored energy in the capacitor
digAnsr: b
Ans : (b) The charge on the capacitor
When we insert a dielectric between the plates of a capacitor, induced charges of opposite polarity appear on the face of the dielectric. They build an electric field inside the dielectric, directed opposite to the original field of the capacitor.
Thus, the net effect is a reduced electric field.
Also, as the potential is proportional to the field, the potential decreases and so does the stored energy U, which is given by
U = `` \frac{qV}{2}``
Thus, only the charge on the capacitor remains unchanged, as the charge is conserved in an isolated system.
Page No 165:

Qstn #3
A dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q‘.
(a) Q‘ may be large than Q.
(b) Q‘ must be larger than Q.
(c) Q‘ must be equal to Q.
(d) Q‘ must be smaller than Q.
digAnsr: d
Ans : (d) Q' must be smaller than Q.
The relation between the induced charge Q' and the charge on the capacitor Q is given by
Q' = `` Q\left(1-\frac{1}{K}\right)``
Here, K is the dielectric constant that is always greater than or equal to 1.
So, we can see that for K > 1, Q' will always be less than Q.
Page No 165:

Qstn #4
Each plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a batter. Now,
(a) the facing surfaces of the capacitor have equal and opposite charges
(b) the two plates of the capacitor have equal and opposite charges
(c) the battery supplies equal and opposite charges to the two plates
(d) the outer surfaces of the plates have equal charges
digAnsr: a,b,d,c
Ans : (a) the facing surfaces of the capacitor have equal and opposite charges
(b) the two plates of the capacitor have equal and opposite charges
(d) the outer surfaces of the plates have equal charges
In H.C Verma the answer is
(a),
(c) ,
(d). But according to us the answer should be
(a),
(b),
(d) all these options are the properties of a capacitor and the option
(c) is incorrect because the battery is a source of energy not charge. Moreover if a capacitor plates have equal charge on outside and equal charge on inside then one can think that the charge on the plates must be also equal so option
(b) cant be incorrect.
Page No 165:

Qstn #5
The separation between the plates of a charged parallel-plate capacitor is increased. Which of the following quantities will change?
(a) Charge on the capacitor
(b) Potential difference across the capacitor
(c) Energy of the capacitor
(d) Energy density between the plates
digAnsr: b,c
Ans : (b) Potential difference across the capacitor
(c) Energy of the capacitor.
Because the charge always remains conserved in an isolated system, it will remain the same.
Now,
V=`` \frac{Qd}{{\in }_{0}A}``
Here, Q, A and d are the charge, area and distance between the plates, respectively.
Thus, as d increases, V increases.
Energy is given by
E = `` \frac{qV}{2}``
So, it will also increase.
Energy density u, that is, energy stored per unit volume in the electric field is given by
u = `` \frac{1}{2}{\in }_{0}{E}^{2}``
So, u will remain constant with increase in distance between the plates.
Page No 165:

Qstn #6
A parallel-plate capacitor is connected to a battery. A metal sheet of negligible thickness is placed between the plates. The sheet remains parallel to the plates of the capacitor.
(a) The battery will supply more charge.
(b) The capacitance will increase.
(c) The potential difference between the plates will increase.
(d) Equal and opposite charges will appear on the two faces of the metal plate.
digAnsr: d
Ans : (d) Equal and opposite charges will appear on the two faces of the metal plate.
The capacitance of the capacitor in which a dielectric slab of dielectric constant K, area A and thickness t is inserted between the plates of the capacitor of area A and separated by a distance d is given by
C = `` \frac{{\in }_{0}A}{\left(d-t\right)+\left(t/K\right)}``
Since it is given that the thickness of the sheet is negligible, the above formula reduces to C = `` \frac{{\in }_{0}A}{d}``. In other words, there will not be any change in the electric field, potential or charge.
Only, equal and opposite charges will appear on the two faces of the metal plate because of induction due to the presence of the charges on the plates of the capacitor.
Page No 165:

Qstn #7
Following operations can be performed on a capacitor:
X - connect the capacitor to a battery of emf ε.
Y - disconnect the battery.
Z - reconnect the battery with polarity reversed.
W - insert a dielectric slab in the capacitor.
(a) In XYZ (perform X, then Y, then Z) the stored electric energy remains unchanged and no thermal energy is developed.
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
digAnsr: b,c,d,a
Ans :
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
Justification of option
(b)
If the potential is held constant, that is, the battery remains attached to the circuit, then the charge on the capacitor increases by a factor of K on inserting a dielectric of a dielectric constant K between the plates of the capacitor.
Mathematically,
q = Kq₀
Here, q₀ and q are the charges without dielectric and with dielectric, respectively.
The amount of charge stored does not depend upon the polarity of the plates.
Thus, the charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
Justification of option
(c)
Since the battery is disconnected before inserting a dielectric, the amount of charge remains constant, that is, q = q₀, because after the battery is disconnected, the capacitor gets no source to store charge from. In other words, the capacitor is now an isolated system where the amount of charge is conserved and so is the energy U as `` \frac{1}{2}``q `` \epsilon ``. Hence, inserting a dielectric after disconnecting the battery will not bring any change in the amount of charge stored in the capacitor. So, the energy stored in the capacitor will also not change after the action XYW.
However, during the action WXY, the amount of charge that will get stored in the capacitor will get increased by a factor of K, as the battery is disconnected after inserting a dielectric between the plates of the capacitor and the energy stored will also get multiplied by a factor of K.
Thus, the electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
Justification of option
(d)
The electric field between the plates E depends on the potential across the capacitor and the distance d between the plates of the capacitor.
Mathematically,
E = `` \frac{\epsilon }{d}``
In either case, that is, during actions XW and WX, the potential remains the same, that is, `` \epsilon ``. Thus, the electric field E remains the same.
Denial of option
(a)
During the action XYZ, the battery has to do extra work equivalent to `` \frac{1}{2}``CV² to change the polarity of the plates of the capacitor. In other words, the total work to be done by the battery will be `` \frac{1}{2}``CV²+ `` \frac{1}{2}``CV². This extra work done will be dissipated as heat energy. Thus, thermal energy is developed. However, the stored electric energy remains unchanged, that is, `` \frac{1}{2}``CV².
Page No 165: