CBSE-XI-Physics
11: Gravitation
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #14Is it necessary for the plane of the orbit of a satellite to pass through the centre of the earth?Ans : According to Kepler first law of planetary motion all planets move in elliptical orbits with sun at one of its foci. It applies to any planet and its satellite as well.This implies that plane of the satellite has to pass through the centre of planet (earth).
Page No 224:
- Qstn #15Consider earth satellites in circular orbits. A geostationary satellite must be at a height of about 36000 km from the earth’s surface. Will any satellite moving at this height be a geostationary satellite? Will any satellite moving at this height have a time period of 24 hours?Ans : `` \text{T=(}\frac{g{R}^{2}{T}^{2}}{4{\,\mathrm{\,\pi \,}}^{2}}{)}^{\frac{1}{3}}-R``
`` T=\frac{4{\,\mathrm{\,\pi \,}}^{2}(\,\mathrm{\,h\,}+\,\mathrm{\,R\,}{)}^{3}}{g{R}^{2}}``
`` =\frac{4\times 3.{14}^{2}\times (36000+6400{)}^{3}\times {10}^{9}}{9.8\times (6400\times {10}^{3}{)}^{2}}``
`` =\text{24.097 Hr}``
`` \text{Which implies that it is a geostationary sattelite with time period=24 Hrs.}``
`` ``
`` ``
Page No 224:
- Qstn #16No part of India is situated on the equator. Is it possible to have a geostationary satellite which always remains over New Delhi?Ans : No. All geostationary orbits are concentric with the equator of the Earth.
Page No 224:
- Qstn #17As the earth rotates about its axis, a person living in his house at the equator goes in a circular orbit of radius equal to the radius of the earth. Why does he/she not feel weightless as a satellite passenger does?Ans : A person living in a house at the equator will not feel weightlessness because he is not in a free fall motion. Satellites are in free fall motion under the gravitational pull of the earth, but, due to the curved surface of the Earth, they move in a circular path. The gravitational force on the satellite due to the Sun provides the centripetal force for its revolution. Therefore, net force on the satellite is zero and, thus, a person feels weightless in a satellite orbiting the earth.
Page No 224:
- Qstn #18Two satellites going in equatorial plane have almost same radii. As seen from the earth one moves from east one to west and the other from west to east. Will they have the same time period as seen from the earth? If not which one will have less time period?Ans : No, both satellites will have different time periods as seen from the Earth. The satellite moving opposite (east to west) to the rotational direction of the Earth will have less time period, because its relative speed with respect to the Earth is more.
Page No 224:
- Qstn #19A spacecraft consumes more fuel in going from the earth to the moon than it takes for a return trip. Comment on this statement.Ans : Yes, a spacecraft consumes more fuel in going from the Earth to the Moon than it takes for the return trip. In going from the Earth to the Moon, the spacecraft has to overcome the gravitational pull of the earth. So, more fuel is consumed in going from the Earth to Moon. However, in the return trip, this gravitation pull helps the spacecraft to come back to the Earth.
Page No 224:
- #Section : ii
- Qstn #1The acceleration of moon with respect to earth is 0⋅0027 m s-2 and the acceleration of an apple falling on earth’ surface is about 10 m s-2. Assume that the radius of the moon is one fourth of the earth’s radius. If the moon is stopped for an instant and then released, it will fall towards the earth. The initial acceleration of the moon towards the earth will be
(a) 10 m s-2
(b) 0â‹…0027 m s-2
(c) 6â‹…4 m s-2
(d) 5â‹…0 m s-2.digAnsr: bAns : (b) 0â‹…0027 m s-2
We know that the distance of the Moon from the Earth is about 60 times the radius of the earth. So, acceleration due to gravity at that distance is 0.0027 m/s2. When the Moon is stopped for an instant and then released, it will fall towards the Earth with an initial acceleration of 0.0027 m/s2.
Page No 224:
- Qstn #2The acceleration of the moon just before it strikes the earth in the previous question is
(a) 10 m s-2
(b) 0â‹…0027 m s-2
(c) 6â‹…4 m s-2
(d) 5â‹…0 m s-2digAnsr: cAns : (c) 6â‹…4 m s-2
According to the previous question, we have:
Radius of the moon, `` {R}_{m}=\frac{{R}_{e}}{4}=\frac{6400000}{4}=1600000\,\mathrm{\,m\,}``
So, when the Moon is just about to hit the surface of the Earth, its centre of mass is at a distance of (Re + Rm) from the centre of the Earth.
Acceleration of the Moon just before hitting the surface of the earth is given by
`` g\text{'}=\frac{GM}{({R}_{e}+{R}_{m}{)}^{2}}=\frac{GM}{{{R}_{e}}^{2}(1+{\displaystyle \frac{{R}_{m}}{{R}_{e}}}{)}^{2}}``
`` \Rightarrow g\text{'}=\frac{g}{(1+{\displaystyle \frac{{R}_{m}}{{R}_{e}}}{)}^{2}}=\frac{10}{(1+{\displaystyle \frac{1}{4}}{)}^{2}}=\frac{10\times 16}{25}``
`` \Rightarrow g\text{'}=6.4\,\mathrm{\,m\,}/{\,\mathrm{\,s\,}}^{2}``
Page No 224:
- Qstn #3Suppose, the acceleration due to gravity at the earth’s surface is 10 m s-2 and at the surface of Mars it is 4⋅0 m s-2. A 60 kg passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky. Which part of figure (11-Q1) best represents the weight (net gravitational force) of the passenger as a function of time?
(a) A
(b) B
(c) C
(d) D.
Figure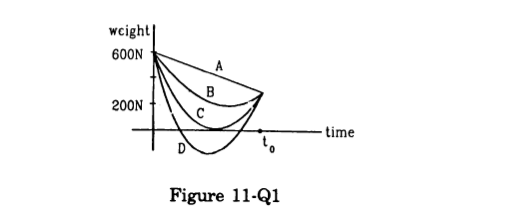
digAnsr: cAns : (c) C
At one point between the Earth and Mars, the gravitational field intensity is zero. So, at that point, the weight of the passenger is zero. The curve C indicates that the weight of the passenger is zero at a point between the Earth and Mars.
Page No 224:
- Qstn #4Consider a planet in some solar system which has a mass double the mass of the earth and density equal to the average density of the earth. An object weighing W on the earth will weight
(a) W
(b) 2 W
(c) W/2
(d) 21/3 W at the planet.digAnsr: dAns : (d) 21/3 W at the planet
The weight of the object on the Earth is `` W=m\frac{G{M}_{e}}{{{R}_{e}}^{2}}``.
Here, m is the actual mass of the object; Me is the mass of the earth and Re is the radius of the earth.
Let Rp be the radius of the planet.
Mass of the planet, `` {M}_{p}=2{M}_{e}``
If `` \rho `` is the average density of the planet then
`` \frac{4}{3}\pi {{R}_{p}}^{3}\times \rho =2\times \left(\frac{4}{3}\pi {{R}_{e}}^{3}\times \rho \right)``
`` \Rightarrow {R}_{p}={\left(2\right)}^{\frac{1}{3}}{R}_{e}``
Now, weight of the body on the planet is given by
`` {W}_{p}=m\left(\frac{G{M}_{p}}{{{R}_{p}}^{2}}\right)=m\left(\frac{2G{M}_{e}}{{2}^{{\displaystyle \frac{2}{3}}}{{R}_{e}}^{2}}\right)``
`` \Rightarrow {W}_{p}={2}^{\frac{1}{3}}\times m\left(\frac{G{M}_{e}}{{{R}_{e}}^{2}}\right)``
`` \Rightarrow {W}_{p}={2}^{\frac{1}{3}}\times W``
Page No 224:
- Qstn #5If the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body of mass m from the earth’s surface to a height R equal to the radius of the earth is
(a)
12mgR
(b)
2mgR
(c)
mgR
(d)
14mgR.digAnsr: aAns : (a) `` \frac{1}{2}mgR``
Work done = `` -``(final potential energy `` -`` initial potential energy)
`` \Rightarrow W=-\left(\frac{GMm}{2R}-\frac{GMm}{R}\right)``
`` \Rightarrow W=\frac{1}{2}\frac{GMm}{R}=\frac{1}{2}mR\times \left(\frac{GM}{{R}^{2}}\right)``
`` \Rightarrow W=\frac{1}{2}mRg\left[\because g=\frac{GM}{{R}^{2}}\right]``
Page No 224:
- Qstn #6A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m s -1 as it reaches A. The work done by the person on the mass is -3 J. The potential at A is
(a) -3 J kg-1
(b) -2 J kg-1
(c) -5 J kg-4
(d) none of these.digAnsr: dAns : The work done by the person is equal to the kinetic energy and the potential energy of the mass of 1 kg at point A.
Let VA be the potential at point A.
`` \,\mathrm{\,Now\,},W=\frac{1}{2}m{v}^{2}+{\left(P.E.\right)}_{\,\mathrm{\,A\,}}``
`` \Rightarrow W=\frac{1}{2}m{v}^{2}+{V}_{\,\mathrm{\,A\,}}\times m``
`` \Rightarrow -3=\frac{1}{2}\times 1\times (2{)}^{2}+{V}_{\,\mathrm{\,A\,}}\times 1``
`` \Rightarrow {V}_{\,\mathrm{\,A\,}}=-5\,\mathrm{\,J\,}/\,\mathrm{\,Kg\,}``
Page No 224:
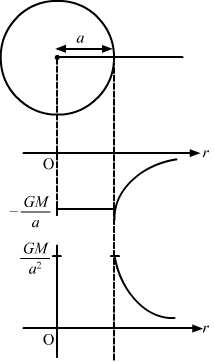
- Qstn #7Let V and E be the gravitational potential and gravitational field at a distance r from the centre of a uniform spherical shell. Consider the following two statements:
(A) The plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
(a) Both A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) Both A and B are wrong.digAnsr: cAns : (c) B is correct but A is wrong.
The plot of E against r is discontinuous as gravitational field inside the spherical shell is zero (r < R). The plot of V against r is a continuous curve for a uniform spherical shell.
Page No 224:
- Qstn #8Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
(a) Both A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) Both A and B are wrong.digAnsr: dAns : (d) Both A and B are wrong.
Both the plots (i.e., V against r and E against r) are continuous curves for a uniform solid sphere.
Page No 224: