CBSE-XI-Physics
10: Rotational Mechanics
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #Section : i
- Qstn #1Can an object be in pure translation as well as in pure rotation?Ans : Yes, such motion is possible if the translation takes place along the axis of rotation. This type of motion is called screw motion.
Page No 192:
- Qstn #2A simple pendulum is a point mass suspended by a light thread from a fixed point. The particle is displaced towards one side and then released. It makes small oscillations. Is the motion of such a simple pendulum a pure rotation? If yes, where is the axis of rotation?Ans : Yes, it is an example of pure rotation.
The axis of rotation passes through the pivot of the pendulum, perpendicular to the plane containing the pendulum.
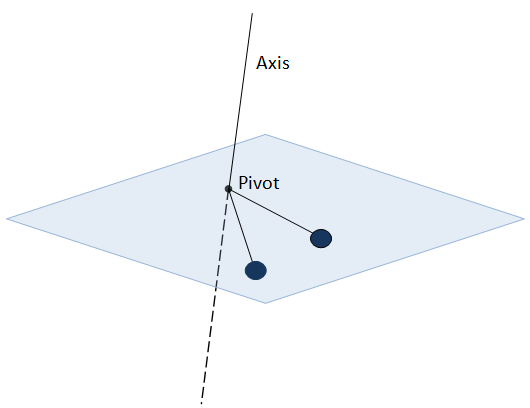
Page No 192:
- Qstn #3In a rotating body,
α=αr and ν=ω r. Thus
αα=νω. Can you use the theorems of ration and proportion studied in algebra so as to write
α+αα-α=ν+ων-ωAns : No, we cannot use componendo-dividendo theorem of proportion here. This is because `` \alpha `` and a, and v and `` \omega `` are dimensionally different. Therefore, v + `` \omega `` and/or `` \alpha `` + a are not possible.
Page No 192:
- Qstn #4A ball is whirled in a circle by attaching it to a fixed point with a string. Is there an angular rotation of the ball about its centre? If yes, is this angular velocity equal to the angular velocity of the ball about the fixed point?Ans : Yes, there is an angular rotation of the ball about its centre.
Yes, angular velocity of the ball about its centre is same as the angular velocity of the ball about the fixed point.
Explanation:
Let the time period of angular rotation of the ball be T.
Therefore, we get:
Angular velocity of the ball about the fixed point = `` \frac{2\pi }{T}``
After one revolution about the fixed centre is completed, the ball has come back to its original position. In this case, the point at which the ball meets with the string is again visible after one revolution. This means that it has undertaken one complete rotation about its centre.
The ball has taken one complete rotation about its centre. Therefore, we have:
Angular displacement of the ball = `` 2\,\mathrm{\,\pi \,}``
Time period = T
So, angular velocity is again `` \frac{2\pi }{T}``. Thus, in both the cases, angular velocities are the same.
Page No 192:
- Qstn #5The moon rotates about the earth in such a way that only one hemisphere of the moon faces the earth (figure 10-Q1). Can we ever see the “other face” of the moon from the earth? Can a person on the moon ever see all the faces of the earth?
Figure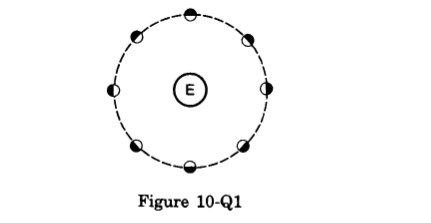
Ans : No, we cannot see the other face of the Moon from the Earth.
Yes, a person on the Moon can see all the faces of the Earth.
Explanation: Angular velocity of the Moon about its own axis of rotation is same as its angular velocity of revolution about the Earth. This means that its rotation time period equals its revolution time period. So, we can see only one face of the Moon from the Earth.
However, angular velocity of the Earth about its axis is not same as the angular velocity of Moon about the Earth. So, all the faces of the Earth is visible from the Moon.
Page No 192:
- Qstn #6The torque of the weight of any body about any vertical axis is zero. If it always correct?Ans : No, its not always correct.
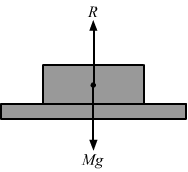
Figure 1
Explanation: If the centre of mass of the body is not on the same vertical line as the normal reaction R of the body, a net torque acts on the body about its vertical axis. In fig. 1, R and CM lies in the same vertical line. Thus, there is no torque about any vertical axis
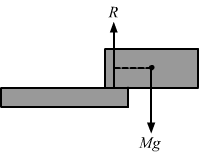
Figure 2
But in fig. 2, as R and CM do not lie along the same vertical line, there exists a torque about the vertical axis.
Page No 192:
- Qstn #7The torque of a force
→Fabout a point is defined as
→Γ=→r×→F. Suppose
→r, →Fand
→Γare all nonzero. Is
r×→Γ||→Falways true? Is it ever true?Ans : `` \,\mathrm{\,No\,},\underset{\,\mathrm{\,r\,}}{\to }\times \underset{\tau }{\to }\left|\right|\underset{\,\mathrm{\,\Gamma \,}}{\to }\,\mathrm{\,is\,}\,\mathrm{\,not\,}\,\mathrm{\,true\,}.``
`` \,\mathrm{\,In\,}\,\mathrm{\,fact\,},\,\mathrm{\,it\,}\,\mathrm{\,is\,}\,\mathrm{\,never\,}\,\mathrm{\,true\,}.\,\mathrm{\,This\,}\,\mathrm{\,is\,}\,\mathrm{\,because\,}:``
`` \underset{\,\mathrm{\,r\,}}{\to }\times \underset{\tau }{\to }``
`` =\underset{\,\mathrm{\,r\,}}{\to }\times \left(\underset{\,\mathrm{\,r\,}}{\to }\times \underset{\,\mathrm{\,F\,}}{\to }\right)``
`` \,\mathrm{\,Applying\,}\,\mathrm{\,vector\,}\,\mathrm{\,triple\,}\,\mathrm{\,product\,},\,\mathrm{\,we\,}\,\mathrm{\,get\,}:``
`` \underset{\,\mathrm{\,r\,}}{\to }\times \left(\underset{\,\mathrm{\,r\,}}{\to }\times \underset{\,\mathrm{\,F\,}}{\to }\right)``
`` =\left(\underset{\,\mathrm{\,r\,}}{\to }.\underset{\,\mathrm{\,F\,}}{\to }\right)\underset{\,\mathrm{\,r\,}}{\to }-\left(\underset{\,\mathrm{\,r\,}}{\to }.\underset{\,\mathrm{\,r\,}}{\to }\right)\underset{\,\mathrm{\,F\,}}{\to }``
`` \because \underset{\,\mathrm{\,r\,}}{\to }.\underset{\,\mathrm{\,r\,}}{\to }={\,\mathrm{\,r\,}}^{2}``
`` =\left(\underset{\,\mathrm{\,r\,}}{\to }.\underset{\,\mathrm{\,F\,}}{\to }\right)\underset{\,\mathrm{\,r\,}}{\to }-{\,\mathrm{\,r\,}}^{2}\underset{\,\mathrm{\,F\,}}{\to }``
`` \,\mathrm{\,If\,}\underset{\,\mathrm{\,r\,}}{\to }.\underset{\,\mathrm{\,F\,}}{\to }=0;\,\mathrm{\,that\,}\,\mathrm{\,is\,},\underset{r}{\to }\perp \underset{\,\mathrm{\,F\,}}{\to },\,\mathrm{\,then\,}:``
`` ``
`` \underset{\,\mathrm{\,r\,}}{\to }\times \underset{\,\mathrm{\,\Gamma \,}}{\to }=-{\,\mathrm{\,r\,}}^{2}\underset{\,\mathrm{\,F\,}}{\to }``
`` \,\mathrm{\,We\,}\,\mathrm{\,know\,}\,\mathrm{\,that\,}{\,\mathrm{\,r\,}}^{2}\,\mathrm{\,is\,}\,\mathrm{\,never\,}\,\mathrm{\,negative\,}\,\mathrm{\,and\,}\underset{\,\mathrm{\,r\,}}{\to }\times \underset{\,\mathrm{\,\Gamma \,}}{\to }=-{\,\mathrm{\,r\,}}^{2}\underset{\,\mathrm{\,F\,}}{\to .}``
`` \,\mathrm{\,This\,}\,\mathrm{\,implies\,}\,\mathrm{\,that\,}\,\mathrm{\,both\,}\,\mathrm{\,vectors\,}\,\mathrm{\,may\,}\,\mathrm{\,be\,}\,\mathrm{\,antiparallel\,}\,\mathrm{\,to\,}\,\mathrm{\,each\,}\,\mathrm{\,other\,}\,\mathrm{\,but\,}\,\mathrm{\,not\,}\,\mathrm{\,parallel\,}.``
`` ``
`` ``
`` ``
Page No 192:
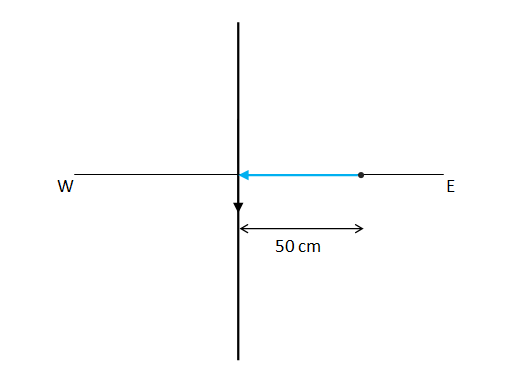
- Qstn #8A heavy particle of mass m falls freely near the earth’s surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?Ans : `` \,\mathrm{\,We\,}\,\mathrm{\,know\,}\,\mathrm{\,that\,}:``
`` \stackrel{\to }{\tau }=\stackrel{\to }{r}\times \stackrel{\to }{F}``
`` \,\mathrm{\,Given\,}:``
`` \stackrel{\to }{r}=-0.5\stackrel{‸}{\,\mathrm{\,i\,}}\,\mathrm{\,m\,}``
`` \stackrel{\to }{F}=-\,\mathrm{\,mg\,}\stackrel{‸}{\,\mathrm{\,j\,}}``
`` \,\mathrm{\,The\,}\,\mathrm{\,torque\,}\,\mathrm{\,becomes\,}:``
`` \stackrel{\to }{\tau }=0.5\left(-\stackrel{‸}{\,\mathrm{\,i\,}}\right)\times mg\left(-\stackrel{‸}{\,\mathrm{\,j\,}}\right)``
`` \stackrel{\to }{\tau }=0.5\,\mathrm{\,mg\,}\stackrel{‸}{\,\mathrm{\,k\,}}\left[\because \stackrel{‸}{\,\mathrm{\,i\,}}\times \stackrel{‸}{\,\mathrm{\,j\,}}=\stackrel{‸}{\,\mathrm{\,k\,}}\right]``
`` \,\mathrm{\,No\,},\,\mathrm{\,there\,}\,\mathrm{\,will\,}\,\mathrm{\,be\,}\,\mathrm{\,no\,}\,\mathrm{\,angular\,}\,\mathrm{\,acceleration\,}\,\mathrm{\,on\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,torque\,}.``
`` \,\mathrm{\,Angular\,}\,\mathrm{\,acceleration\,}\,\mathrm{\,is\,}\,\mathrm{\,given\,}\,\mathrm{\,by\,}\,\mathrm{\,\alpha \,}=\frac{\tau }{I}.\,\mathrm{\,As\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,here\,}\,\mathrm{\,moves\,}\,\mathrm{\,in\,}\,\mathrm{\,a\,}``
`` \,\mathrm{\,straight\,}\,\mathrm{\,line\,},\,\mathrm{\,the\,}\,\mathrm{\,centre\,}\,\mathrm{\,of\,}\,\mathrm{\,rotation\,}\,\mathrm{\,lies\,}\,\mathrm{\,at\,}\,\mathrm{\,a\,}\,\mathrm{\,distance\,}\,\mathrm{\,infinity\,}(r=\infty );\,\mathrm{\,so\,},\,\mathrm{\,moment\,}\,\mathrm{\,of\,}\,\mathrm{\,inertia\,}(I=m{r}^{2})\,\mathrm{\,of\,}\,\mathrm{\,the\,}``
`` \,\mathrm{\,particle\,}\,\mathrm{\,is\,}\,\mathrm{\,infinity\,}.``
`` \therefore \alpha =0``
Page No 192:
- Qstn #9If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?Ans :
`` \,\mathrm{\,Suppose\,}\stackrel{\to }{{f}_{1}},\stackrel{\to }{{f}_{2}},\stackrel{\to }{{f}_{3}},...\stackrel{\to }{{f}_{n}}\,\mathrm{\,be\,}\,\mathrm{\,the\,}\,\mathrm{\,forces\,}\,\mathrm{\,acting\,}\,\mathrm{\,on\,}\,\mathrm{\,a\,}\,\mathrm{\,point\,}P.``
`` \,\mathrm{\,Suppose\,}O\,\mathrm{\,be\,}\,\mathrm{\,the\,}\,\mathrm{\,point\,}\,\mathrm{\,along\,}\,\mathrm{\,which\,}\,\mathrm{\,torques\,}\left(\,\mathrm{\,moments\,}\right)\,\mathrm{\,will\,}\,\mathrm{\,be\,}\,\mathrm{\,taken\,}.``
`` \,\mathrm{\,Suppose\,}:``
`` \stackrel{\to }{{f}_{1}}+\stackrel{\to }{{f}_{2}}+\stackrel{\to }{{f}_{3}}+...+\stackrel{\to }{{f}_{n}}=\stackrel{\to }{R}...\left(1\right)``
`` \,\mathrm{\,Moments\,}\,\mathrm{\,of\,}\,\mathrm{\,force\,}\left(\,\mathrm{\,torque\,}\right)\stackrel{\to }{{f}_{i}}\,\mathrm{\,about\,}O\,\mathrm{\,will\,}\,\mathrm{\,be\,}:``
`` \stackrel{\to }{{\tau }_{1}}=\stackrel{\to }{\,\mathrm{\,OP\,}}\times \stackrel{\to }{{f}_{1}}``
`` \,\mathrm{\,The\,}\,\mathrm{\,sum\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,torques\,}\,\mathrm{\,about\,}O\,\mathrm{\,will\,}\,\mathrm{\,be\,}:``
`` \stackrel{\to }{M}=\stackrel{\to }{\,\mathrm{\,OP\,}}\times \stackrel{\to }{{f}_{1}}+\stackrel{\to }{\,\mathrm{\,OP\,}}\times \stackrel{\to }{{f}_{2}}+...+\stackrel{\to }{\,\mathrm{\,OP\,}}\times \stackrel{\to }{{f}_{n}}``
`` \Rightarrow \stackrel{\to }{M}=\stackrel{\to }{\,\mathrm{\,OP\,}}\times \left(\stackrel{\to }{{f}_{1}}+\stackrel{\to }{{f}_{2}}+\stackrel{\to }{{f}_{3}}+...+\stackrel{\to }{{f}_{n}}\right)``
`` \Rightarrow \stackrel{\to }{M}=\stackrel{\to }{\,\mathrm{\,OP\,}}\times \stackrel{\to }{R}\left[\,\mathrm{\,From\,}\left(1\right)\right]``
`` \,\mathrm{\,Thus\,},\,\mathrm{\,we\,}\,\mathrm{\,see\,}\,\mathrm{\,that\,}\,\mathrm{\,the\,}\,\mathrm{\,torque\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,resultant\,}\,\mathrm{\,force\,}\stackrel{\to }{\,\mathrm{\,R\,}}\,\mathrm{\,of\,}\,\mathrm{\,the\,}``
`` \,\mathrm{\,forces\,}\stackrel{\to }{{f}_{1}},\stackrel{\to }{{f}_{2}},\stackrel{\to }{{f}_{3}},...\stackrel{\to }{,{f}_{n}}\,\mathrm{\,gives\,}\,\mathrm{\,the\,}\,\mathrm{\,sum\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,moments\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,torques\,}.``
Page No 192:
- Qstn #10If the sum of all the forces acting on a body is zero, is it necessarily in equilibrium? If the sum of all the forces on a particle is zero, is it necessarily in equilibrium?Ans : `` \,\mathrm{\,No\,},\,\mathrm{\,if\,}\,\mathrm{\,the\,}\,\mathrm{\,sum\,}\,\mathrm{\,of\,}\,\mathrm{\,all\,}\,\mathrm{\,the\,}\,\mathrm{\,forces\,}\,\mathrm{\,acting\,}\,\mathrm{\,on\,}\,\mathrm{\,a\,}\,\mathrm{\,body\,}\,\mathrm{\,is\,}z\,\mathrm{\,ero\,},\,\mathrm{\,the\,}\,\mathrm{\,body\,}\,\mathrm{\,is\,}\,\mathrm{\,not\,}\,\mathrm{\,necessarily\,}\,\mathrm{\,in\,}\,\mathrm{\,equilibrium\,}.\,\mathrm{\,To\,}\,\mathrm{\,be\,}\,\mathrm{\,in\,}\,\mathrm{\,equilibrium\,},``
`` \,\mathrm{\,the\,}\,\mathrm{\,sum\,}\,\mathrm{\,of\,}\,\mathrm{\,torque\,}\,\mathrm{\,acting\,}\,\mathrm{\,on\,}\,\mathrm{\,the\,}\,\mathrm{\,body\,}\,\mathrm{\,must\,}\,\mathrm{\,be\,}z\,\mathrm{\,ero\,}\,\mathrm{\,too\,}(s\,\mathrm{\,ee\,}\,\mathrm{\,the\,}\,\mathrm{\,fig\,}.).\,\mathrm{\,In\,}\,\mathrm{\,the\,}\,\mathrm{\,above\,}\,\mathrm{\,case\,},\,\mathrm{\,although\,}\,\mathrm{\,the\,}\,\mathrm{\,sum\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,forces\,}\,\mathrm{\,acting\,}``
`` \,\mathrm{\,on\,}\,\mathrm{\,the\,}\,\mathrm{\,body\,}\,\mathrm{\,is\,}\,\mathrm{\,zero\,}(\stackrel{\to }{{\,\mathrm{\,F\,}}_{1}}+\left(-\stackrel{\to }{{\,\mathrm{\,F\,}}_{1}}\right)=0).\,\mathrm{\,Still\,},\,\mathrm{\,the\,}\,\mathrm{\,body\,}\,\mathrm{\,will\,}\,\mathrm{\,rotate\,}\,\mathrm{\,along\,}\stackrel{\to }{\,\mathrm{\,OP\,}}.\,\mathrm{\,So\,},\,\mathrm{\,it\,}\,\mathrm{\,won\,}\text{'}\,\mathrm{\,t\,}\,\mathrm{\,remain\,}\,\mathrm{\,in\,}\,\mathrm{\,equilibrium\,}.``
Page No 192:
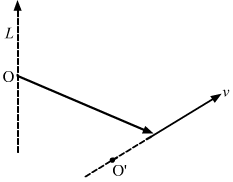
- Qstn #11If the angular momentum of a body is found to be zero about a point, is it necessary that it will also be zero about a different point?Ans : No, angular momentum is dependent on the position vector of the particle, angle between the radius vector and the linear velocity of the particle. So, there may be finite angular momentum along any different point even if it is zero at a particular point.If angular momentum is zero along O' but finite along O.
Page No 192:
- Qstn #12If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?Ans : `` \,\mathrm{\,No\,},\,\mathrm{\,it\,}\,\mathrm{\,is\,}\,\mathrm{\,not\,}\,\mathrm{\,necessary\,}\,\mathrm{\,that\,}\,\mathrm{\,the\,}\,\mathrm{\,torque\,}\,\mathrm{\,about\,}\,\mathrm{\,any\,}\,\mathrm{\,other\,}\,\mathrm{\,point\,}\,\mathrm{\,be\,}\,\mathrm{\,zero\,}\,\mathrm{\,if\,}\,\mathrm{\,it\,}\,\mathrm{\,is\,}\,\mathrm{\,zero\,}\,\mathrm{\,about\,}\,\mathrm{\,one\,}\,\mathrm{\,point\,}.``
`` ``
`` \,\mathrm{\,Suppose\,}\stackrel{\to }{F}\,\mathrm{\,be\,}\,\mathrm{\,the\,}\,\mathrm{\,resultant\,}\,\mathrm{\,force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,all\,}\,\mathrm{\,the\,}\,\mathrm{\,forces\,}\,\mathrm{\,acting\,}\,\mathrm{\,on\,}\,\mathrm{\,the\,}\,\mathrm{\,plane\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,body\,}.\,\mathrm{\,Therefore\,},\,\mathrm{\,torque\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,force\,}\stackrel{\to }{F}\,\mathrm{\,at\,}\,\mathrm{\,any\,}\,\mathrm{\,point\,}``
`` \,\mathrm{\,will\,}\,\mathrm{\,be\,}\,\mathrm{\,the\,}\,\mathrm{\,resultant\,}\,\mathrm{\,torque\,}.\,\mathrm{\,Now\,},\,\mathrm{\,we\,}\,\mathrm{\,see\,}\,\mathrm{\,that\,}\,\mathrm{\,the\,}\,\mathrm{\,torque\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\stackrel{\to }{F}\,\mathrm{\,at\,}\,\mathrm{\,point\,}Q\,\mathrm{\,will\,}\,\mathrm{\,be\,}\,\mathrm{\,zero\,}\,\mathrm{\,because\,}Q\,\mathrm{\,lies\,}\,\mathrm{\,on\,}\,\mathrm{\,the\,}\,\mathrm{\,line\,}\,\mathrm{\,of\,}\,\mathrm{\,support\,}\,\mathrm{\,of\,}``
`` \,\mathrm{\,the\,}\,\mathrm{\,force\,}F\,\mathrm{\,but\,}\,\mathrm{\,the\,}\,\mathrm{\,torque\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,force\,}\stackrel{\to }{F}\,\mathrm{\,will\,}\,\mathrm{\,not\,}\,\mathrm{\,be\,}\,\mathrm{\,zero\,}\,\mathrm{\,along\,}\,\mathrm{\,the\,}\,\mathrm{\,point\,}P.``
Page No 192:
- Qstn #13A body is in translational equilibrium under the action of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?Ans : `` \,\mathrm{\,Yes\,},\,\mathrm{\,if\,}\,\mathrm{\,the\,}\,\mathrm{\,torque\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,forces\,}\,\mathrm{\,in\,}\,\mathrm{\,translation\,}\,\mathrm{\,equillibrium\,}``
`` \,\mathrm{\,is\,}\,\mathrm{\,zero\,}\,\mathrm{\,about\,}\,\mathrm{\,a\,}\,\mathrm{\,point\,},\,\mathrm{\,it\,}\,\mathrm{\,will\,}\,\mathrm{\,be\,}\,\mathrm{\,zero\,}\,\mathrm{\,about\,}\,\mathrm{\,other\,}\,\mathrm{\,point\,}\,\mathrm{\,in\,}\,\mathrm{\,the\,}\,\mathrm{\,plane\,}.``
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,us\,}\,\mathrm{\,consider\,}\,\mathrm{\,a\,}\,\mathrm{\,planner\,}\,\mathrm{\,lamina\,}\,\mathrm{\,of\,}\,\mathrm{\,some\,}\,\mathrm{\,mass\,},\,\mathrm{\,acted\,}\,\mathrm{\,upon\,}\,\mathrm{\,by\,}``
`` \,\mathrm{\,forces\,}\stackrel{\to }{{F}_{1}},\stackrel{\to }{{F}_{2}},...\stackrel{\to }{{F}_{i}},\,\mathrm{\,etc\,}.``
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,a\,}\,\mathrm{\,force\,}\stackrel{\to }{{F}_{i}}\,\mathrm{\,act\,}\,\mathrm{\,on\,}\,\mathrm{\,a\,}{\,\mathrm{\,i\,}}^{\,\mathrm{\,th\,}}\,\mathrm{\,particle\,}\,\mathrm{\,and\,}\,\mathrm{\,torque\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\stackrel{\to }{{F}_{i}}\,\mathrm{\,be\,}\,\mathrm{\,zero\,}``
`` \,\mathrm{\,at\,}\,\mathrm{\,a\,}\,\mathrm{\,point\,}\,\mathrm{\,Q\,}.``
`` \,\mathrm{\,Since\,}\,\mathrm{\,the\,}\,\mathrm{\,body\,}\,\mathrm{\,is\,}\,\mathrm{\,in\,}\,\mathrm{\,translation\,}\,\mathrm{\,equillibrium\,},\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
`` \,\mathrm{\,\Sigma \,}\stackrel{\to }{{F}_{i}}=0...\left(1\right)``
`` \,\mathrm{\,Again\,},\,\mathrm{\,torque\,}\,\mathrm{\,about\,}\,\mathrm{\,P\,}\,\mathrm{\,is\,}\,\mathrm{\,zero\,}.\,\mathrm{\,Therefore\,},\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
`` \,\mathrm{\,\Sigma \,}\left(\stackrel{\to }{{r}_{pi}}\times \stackrel{\to }{{F}_{i}}\right)=0...\left(2\right)``
`` \,\mathrm{\,Now\,},\,\mathrm{\,torque\,}\,\mathrm{\,about\,}\,\mathrm{\,point\,}\,\mathrm{\,Q\,}\,\mathrm{\,will\,}\,\mathrm{\,be\,}:``
`` \,\mathrm{\,\Sigma \,}{\stackrel{\to }{r}}_{\,\mathrm{\,Qi\,}}\times \stackrel{\to }{{F}_{i}}``
`` =\,\mathrm{\,\Sigma \,}\left({\stackrel{\to }{r}}_{QP}+{\stackrel{\to }{r}}_{Pi}\right)\times \stackrel{\to }{{F}_{i}}\left[\,\mathrm{\,From\,}\,\mathrm{\,fig\,}.13\right]``
`` =\Sigma \left({\stackrel{\to }{r}}_{QP}\times \stackrel{\to }{{F}_{i}}+\stackrel{\to }{{r}_{Pi}}\times \stackrel{\to }{{F}_{i}}\right)``
`` =\,\mathrm{\,\Sigma \,}\stackrel{\to }{{r}_{QP}}\times \stackrel{\to }{{F}_{i}}+\Sigma \stackrel{\to }{{r}_{Pi}}\times \stackrel{\to }{{F}_{i}}``
`` =\stackrel{\to }{{r}_{\,\mathrm{\,QP\,}}}\times \,\mathrm{\,\Sigma \,}\stackrel{\to }{{F}_{i}}+0\left[\,\mathrm{\,From\,}\left(2\right)\right]``
`` =\stackrel{\to }{{r}_{QP}}\times 0\left[\,\mathrm{\,From\,}\left(1\right)\right]``
`` =0``
`` \,\mathrm{\,Thus\,},\stackrel{\to }{F}\,\mathrm{\,is\,}\,\mathrm{\,zero\,}\,\mathrm{\,about\,}\,\mathrm{\,any\,}\,\mathrm{\,other\,}\,\mathrm{\,point\,}\,\mathrm{\,Q\,}.``
Page No 192: