HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
CBSE-XI-Physics

07: Circular Motion

with Solutions - page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #3
    A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.
    (a) NA = NB
    (b) NA > NB
    (c) NA < NB
    (d) insufficient
    Figure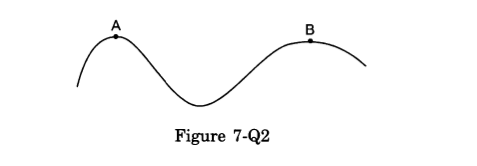
    digAnsr:   c
    Ans : (c) NA < NB
    From the figure in the question, it is clear that `` {r}_{B}>{r}_{A}``.
    Here, normal reaction is inversely proportional to the centrifugal force acting on the car, while taking turn on the curve track. Also, centrifugal force is inversely proportional to the radius of the circular track.
    Therefore, we have:
    NA < NB
  • Qstn #4
    A particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a uniform speed v. The centrifugal force on it is
    (a)``mv^2r`` towards the centre
    (b) ``mv^2r`` away from the centre
    (c)``mv^2r`` along the tangent through the particle
    (d) zero
    digAnsr:   d
    Ans : (d) zero
    The centrifugal force is a pseudo force and can only be observed from the frame of reference, which is non-inertial w.r.t. the particle.
  • Qstn #5
    A particle of mass m rotates with a uniform angular speed ω. It is viewed from a frame rotating about the Z-axis with a uniform angular speed ω0. The centrifugal force on the particle is
    (a) mω2a
    (b)
    mω02a(c)
    mω+ω022a(d) mω ω0 a.
    digAnsr:   b
    Ans : (b) `` m{\,\mathrm{\,\omega \,}}_{0}^{2}\,\mathrm{\,a \,}``
    The centrifugal force on the particle depends on the angular speed (ω0) of the frame and not on the angular speed (ω) of the particle. Thus, the value of centrifugal force on the particle is `` m{\,\mathrm{\,\omega \,}}_{0}^{2}\,\mathrm{\,a \,}``.
  • Qstn #6
    A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
    (a) 10 cm/s, 10 cm/s2
    (b) 10 cm/s, 80 cm/s2
    (c) 40 cm/s, 10 cm/s2
    (d) 40 cm/s, 40 cm/s2
    digAnsr:   a
    Ans : (a) 10 cm/s, 10 cm/s2
    It is given that the turntable is rotating with uniform angular velocity. Let the velocity be `` \omega ``.
    We have:
    `` v=r\omega ``
    `` \Rightarrow v\propto r(\,\mathrm{\,for \,}\,\mathrm{\,constant \,}\omega )``
    `` \frac{v}{v\text{ ' }}=\frac{r}{r\text{ ' }}``
    `` \Rightarrow v\text{ ' }=\frac{v}{2}=10\,\mathrm{\,cm \,}/\,\mathrm{\,s \,}``
    Similarly, we have:
    `` a\text{ ' }=\frac{a}{2}=10\,\mathrm{\,cm \,}/{\,\mathrm{\,s \,}}^{2}``
  • Qstn #7
    Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
    (a) ``mg=mv^2r``
    (b) mg is greater than ``mv^2r``
    (c) mg is not greater than ``mv^2r``
    (d) mg is not less than ``mv^2r``.
    digAnsr:   c
    Ans : (c) mg is not greater than `` \frac{m{v}^{2}}{r}``
    At the top of the path, the direction of mg is vertically downward and for centrifugal force `` \left(\frac{m{v}^{2}}{r}\right)``, the direction is vertically upward. If the vertically downward force is not greater, water will not fall.
    Page No 113:
  • Qstn #8
    A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
    (a) towards the centre
    (b) away from the centre
    (c) along a tangent
    (d) will stop.
    digAnsr:   c
    Ans : (c) along a tangent
    The stone will move in a circle and the direction of velocity at any instant is always along the tangent at that point. Therefore, the stone will move along the tangent to the circle at a point where the string breaks.
    Page No 113:
  • Qstn #9
    A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
    (a) 1 cm
    (b) 2 cm
    (c) 4 cm
    (d) 8 cm
    digAnsr:   a
    Ans : (a) 1 cm
    Let the force of friction between the coin and the rotating turntable be F.
    For the coin to just slip, we have:
    `` F=m{\omega }^{2}r``
    Here, `` m{\omega }^{2}r``is the centrifugal force acting on the coin.
    For constant F and m, we have:
    `` r\propto \frac{1}{{\omega }^{2}}``
    Therefore,
    `` \frac{r\text{ ' }}{r}={\left({\displaystyle \frac{\omega }{\omega \text{ ' }}}\right)}^{2}``
    `` \Rightarrow r\text{ ' }=1\,\mathrm{\,cm \,}``
    Page No 113:
  • Qstn #10
    A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
    (a) increases
    (b) decreases
    (c) remains the same
    (d) fluctuates.
    digAnsr:   a
    Ans : (a) increases

    The normal force on the motorcycle, `` N=mg\,\mathrm{\,cos \,}\theta -\frac{m{v}^{2}}{R}``
    As the motorcycle is ascending on the overbridge, θ decreases (from `` \frac{\pi }{2}`` to 0).
    So, normal force increases with decrease in θ.
    Page No 113:
  • Qstn #11
    Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
    (a) FA is maximum of the three forces.
    (b) FB is maximum of the three forces.
    (c) FC is maximum of the three forces.
    (d) FA = FB = FC.
    digAnsr:   c
    Ans : (c) FC is maximum of the three forces.
    At the middle of bridge, normal force can be given as:
    `` {N}_{A}=mg``
    `` {N}_{B}=\frac{m{v}^{2}}{r}-mg``
    `` {N}_{C}=\frac{m{v}^{2}}{r}+mg``
    `` ``
    So, FC is maximum.

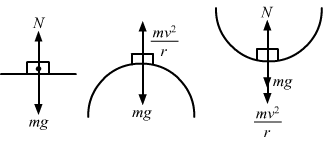
    Page No 113:
  • Qstn #12
    A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
    (a) F1 > F2.
    (b) F1 < F2
    (c) F1 = F2
    (d) the information is insufficient to find the relation between F1 and F2.
    digAnsr:   a
    Ans : (a) F1 > F2
    When the trains are moving, effective angular velocity of both the trains are different (as shown in the figure).

    Effective angular velocity of train B is more than that of train A.
    Normal force with which both the trains push the tracks is given as:
    `` N=mg-mR\omega {\text{ ' }}^{2}``
    From the above equation, we can conclude that F1 > F2.
    Page No 113:
  • Qstn #13
    If the earth stop rotating, the apparent value of g on its surface will
    (a) increase everywhere
    (b) decrease everywhere
    (c) remain the same everywhere
    (d) increase at some places and remain the same at some other places.
    digAnsr:   d
    Ans : (d) increase at some places and remain the same at some other places
    If the Earth stops rotating on its axis, there will be an increase in the value of acceleration due to gravity at the equator. At the same time, there will be no change in the value of g at the poles.
    Page No 113:
  • Qstn #14
    A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
    (a) T1 > T2
    (b) T2 > T1
    (c) T1 = T2
    (d) The relation between T1 and T2 depends on whether the rod rotates clockwise or anticlockwise.
    digAnsr:   a
    Ans : (a) T1 > T2

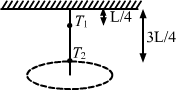
    Let the angular velocity of the rod be `` \omega ``.
    Distance of the centre of mass of portion of the rod on the right side of L/4 from the pivoted end:
    `` {r}_{1}=\frac{L}{4}+\frac{1}{2}\left(\frac{3L}{4}\right)=\frac{5L}{8}``
    Mass of the rod on the right side of L/4 from the pivoted end:
    `` {m}_{1}=\frac{3}{4}M``
    At point L/4, we have:
    `` {T}_{1}={m}_{1}{\omega }^{2}{r}_{1}``
    `` =\frac{3}{4}M{\omega }^{2}\frac{5}{8}L=\frac{15}{32}M{\omega }^{2}L``
    Distance of the centre of mass of rod on the right side of 3L/4 from the pivoted end:
    `` {r}_{1}=\frac{1}{2}\left(\frac{L}{4}\right)+\frac{3L}{4}=\frac{7L}{8}``
    Mass of the rod on the right side of L/4 from the pivoted end:
    `` {m}_{1}=\frac{1}{4}M``
    At point 3L/4, we have:
    `` {T}_{2}={m}_{2}{\omega }^{2}{r}_{2}``
    `` =\frac{1}{4}M{\omega }^{2}\frac{7}{8}L=\frac{7}{32}M{\omega }^{2}L``
    ∴ T1 > T2
    Page No 113:
  • Qstn #15
    A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
    (a) mg
    (b)mg-``mv^2R``
    (c)mg+``mv^2R``
    (d) zero.
    digAnsr:   d
    Ans : (d) zero
    When the car is in air, the acceleration of bob and car is same. Hence, the tension in the string will be zero.
    Page No 113:
  • Qstn #16
    Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
    (a) always
    (b) never
    (c) at the extreme positions
    (d) at the mean position.
    digAnsr:   c
    Ans : (c) at the extreme positions
    Tension is the string, `` T=\frac{m{v}^{2}}{r}-mg\,\mathrm{\,cos \,}\theta ``
    When v = 0, `` \left|T\right|=mg\,\mathrm{\,cos \,}\theta ``
    That is, at the extreme positions, the tension is the string is mgcosθ.
    Page No 113:
  • #
    Section : iii
next page