CBSE-XI-Physics
04: The Forces
- #6Suppose the magnitude of Nuclear force between two protons varies with the distance between them as shown in figure. Estimate the ratio “Nuclear force/Coulomb force” for (a) x = 8 fm (b) x = 4 fm (c) x = 2 fm (d) x = 1 fm (1 fm = 10 -15m).
Figure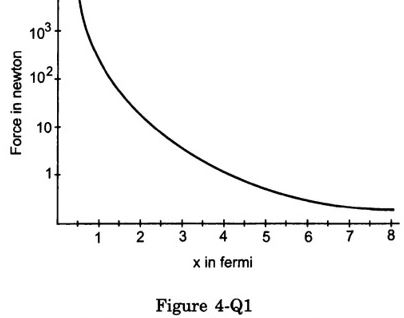 Ans : First let us calculate the coulomb force between 2 protons for distance = 8 fm
Ans : First let us calculate the coulomb force between 2 protons for distance = 8 fm
`` F\mathit{}\mathit{=}\frac{\mathit{K}\mathit{}{\mathit{q}}^{\mathit{2}}}{{\mathit{r}}^{\mathit{2}}}``
`` =\frac{9\times {10}^{9}\times (1.6\times {10}^{-19}{)}^{2}}{(8\times {10}^{-15}{)}^{2}}``
`` =3.6\,\mathrm{\,N \,}``
`` {F}_{\,\mathrm{\,N \,}}=0.05\,\mathrm{\,N \,}``
`` \frac{{F}_{\,\mathrm{\,N \,}}}{{F}_{\,\mathrm{\,C \,}}}=\frac{0.05}{3.6}=0.0138\,\mathrm{\,N \,}``
For x= 4 fm
`` {F}_{\,\mathrm{\,C \,}}=\frac{9\times {10}^{9}\times (1.6\times {10}^{-19}{)}^{2}}{(4\times {10}^{-15}{)}^{2}}``
`` =\frac{23.04\times {10}^{-29}}{(4\times {10}^{-15}{)}^{2}}``
`` =14.4\,\mathrm{\,N \,}``
`` {F}_{\,\mathrm{\,N \,}}=1\,\mathrm{\,N \,}``
`` \frac{{F}_{\,\mathrm{\,N \,}}}{{F}_{\,\mathrm{\,C \,}}}=\frac{1}{14.4}=0.0694\,\mathrm{\,N \,}``
`` \,\mathrm{\,For \,}x=2\,\mathrm{\,fm \,}``
`` {F}_{\,\mathrm{\,C \,}}=\frac{9\times {10}^{9}\times (1.6\times {10}^{-19}{)}^{2}}{(2\times {10}^{-15}{)}^{2}}``
`` =57.6\,\mathrm{\,N \,}``
`` {F}_{\,\mathrm{\,N \,}}=10\,\mathrm{\,N \,}``
`` \frac{{F}_{\,\mathrm{\,N \,}}}{{F}_{\,\mathrm{\,C \,}}}=\frac{10}{57.6}=0.173``
`` \,\mathrm{\,For \,}x=1\,\mathrm{\,fm \,}``
`` {F}_{\,\mathrm{\,C \,}}=\frac{9\times {10}^{9}\times (1.6\times {10}^{-19}{)}^{2}}{(1\times {10}^{-15}{)}^{2}}``
`` =230.4\,\mathrm{\,N \,}``
`` {F}_{\,\mathrm{\,N \,}}=1000\,\mathrm{\,N \,}``
`` \frac{{F}_{\,\mathrm{\,N \,}}}{{F}_{\,\mathrm{\,C \,}}}=\frac{1000}{230.4}=4.34``