CBSE-XI-Physics
03: Rest and Motion: Kinematics
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #11Two projectiles A and B are projected with angle of projection 15° for the projectile A and 45° for the projectile B. If RA and RB be the horizontal range for the two projectiles, then
-(a) RA < RB
(b) RA > RB
(c) RA = RB
(d) the information is insufficient to decide the relation ofRA with RB.digAnsr: dAns : (d) The information is insufficient to decide the relation of RA with RB.
Horizontal range for the projectile, `` R=\frac{{u}^{2}\,\mathrm{\,sin \,}\left(2\alpha \right)}{g}``
Information of the initial velocity is not given in the question.
- Qstn #12A river is flowing from west to east at a speed of 5 metres per minute. A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
-(a) due north
(b) 30° east of north
(c) 30° north of west
(d) 60° east of north.digAnsr: aAns : (a) due north
If the man swims at any angle east to the north direction, although his relative speed will increase, he will have to travel a larger distance. So, he will take more time.
If the man swims at any angle west to the north direction, his relative speed will decrease. So, he will take more time.
- Qstn #13In the arrangement shown in figure the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed
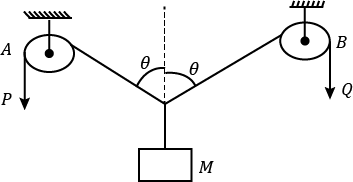
-(a) 2u cos θ
(b) u/cos θ
(c) 2u/cos θ
(d) u cos θ
digAnsr: bAns : (b) `` v=\frac{u}{\,\mathrm{\,cos \,}\left(\theta \right)}``

Along the string, the velocity of each object is the same.
`` 2v\,\mathrm{\,cos \,}\left(\theta \right)=2u``
`` v=\frac{u}{\,\mathrm{\,cos \,}\left(\theta \right)}``
- #Section : CObjective II
- Qstn #1Consider the motion of the tip of the minute hand of a clock. In one hour
--(a) the displacement is zero
(b) the distance covered is zero
(c) the average speed is zero
(d) the average velocity is zerodigAnsr: a,dAns : (a) the displacement is zero
(d) the average velocity is zero
Displacement is zero because the initial and final positions are the same.
Average velocity = `` \frac{\,\mathrm{\,Displacement \,}}{\,\mathrm{\,Total \,}\,\mathrm{\,time \,}}=0``
Distance covered = `` 2\,\mathrm{\,\pi \,}r`` ≠ 0
Average speed =`` \frac{\,\mathrm{\,Distance \,}\,\mathrm{\,travelled \,}}{\,\mathrm{\,Total \,}\,\mathrm{\,time \,}\,\mathrm{\,taken \,}}\ne 0``
- Qstn #2A particle moves along the X-axis as
x = u (t - 2 s) + a (t - 2 s)2.
--(a) the initial velocity of the particle is u
(b) the acceleration of the particle is a
(c) the acceleration of the particle is 2a
(d) at t = 2 s particle is at the origin.digAnsr: c,dAns : (c) the acceleration of the particle is 2a
(d) at t = 2 s, the particle is at the origin
Initial velocity = `` {\left|\frac{dx}{dt}\right|}_{t=0}``
`` \frac{dx}{dt}=u+2a(t-2s)``
`` {\left|\frac{dx}{dt}\right|}_{t=0}=u-4as\ne u``
Acceleration =`` \frac{{d}^{2}x}{d{t}^{2}}=2a``
At t = 2 s,
x = u(2 s - 2 s) + a (2 s - 2 s)2 = 0 (origin)
- Qstn #3Pick the correct statements:
--(a) Average speed of a particle in a given time is never less than the magnitude of the average velocity.
(b) It is possible to have a situation in which
dv→dt≠0butddt=v→=0
(c) The average velocity of a particle is zero in a time interval. It is possible that the instantaneous velocity is never zero is the interval.
(d) The average velocity of a particle moving on a straight line is zero in a time interval. It is possible that the instantaneous velocity is never zero in the interval. (Infinite accelerations are not allowed).digAnsr: a,b,cAns : (a) Average speed of a particle in a given time is never less than the magnitude of the average velocity.
(b) It is possible to have a situation in which `` \left|\frac{d\stackrel{\to }{v}}{dt}\right|\ne 0\,\mathrm{\,but \,}\frac{d}{dt}\left|\stackrel{\to }{v}\right|=0``.
(c) The average velocity of a particle is zero in a time interval. It is possible that the instantaneous velocity is never zero in the interval, for example, the motion of a particle on a circular track with a constant speed.
Average velocity = `` \frac{\,\mathrm{\,Displacement \,}}{\,\mathrm{\,Total \,}\,\mathrm{\,time \,}}``
Displacement ≤ Distance
`` \therefore `` Average velocity ≤ Average speed
In uniform circular motion, speed is constant but velocity is not.
i.e., `` \left|\frac{d\stackrel{\to }{v}}{dt}\right|\ne 0\,\mathrm{\,but \,}\frac{d}{dt}=\left|\stackrel{\to }{v}\right|=0`` which proves case (b)
(d) In one complete circle of uniform motion, average velocity is zero. Instantaneous velocity is never zero in the interval.
- Qstn #4An object may have
--(a) varying speed without having varying velocity
(b) varying velocity without having varying speed
(c) nonzero acceleration without having varying velocity
(d) nonzero acceleration without having varying speed.digAnsr: b,dAns : (b) varying velocity without having varying speed
(d) nonzero acceleration without having varying speed
Velocity and acceleration are vector quantities that can be changed by changing direction only (keeping magnitude constant).
- Qstn #5Mark the correct statements for a particle going on a straight line:
--(a) If the velocity and acceleration have opposite sign, the object is slowing down.
(b) If the position and velocity have opposite sign the particle is moving towards the origin.
(c) If the velocity is zero at an instant, the acceleration should also be zero at that instant.
(d) If the velocity is zero for a time interval, the acceleration is zero at any instant within the time interval.digAnsr: a,b,dAns : (a) If the velocity and acceleration have opposite signs, the object slows down.
(b) If the position and velocity have opposite signs, the particle moves towards the origin.
(d) If the velocity is zero for a time interval, the acceleration is zero at any instant within the time interval.
(a) Acceleration is given by
`` -a=\frac{dv}{dt}``
`` -a<0``
`` \Rightarrow \frac{dv}{dt}<0``
`` \Rightarrow {V}_{\,\mathrm{\,final \,}}<{V}_{\,\mathrm{\,initial \,}}``
(b) If the position and velocity have opposite signs, the particle moves towards the origin. It can be explained by following figure:

(c) If the velocity is zero in a certain time interval, then the change in the velocity in that time interval will also be zero. As acceleration is rate of change of velocity, it will also be zero at an instant in that time interval.
- Qstn #6The velocity of a particle is zero at t = 0.
--(a) The acceleration at t = 0 must be zero.
(b) The acceleration at t = 0 may be zero.
(c) If the acceleration is zero from t = 0 to t = 10 s, the speed is also zero in this interval.
(d) If the speed is zero from t = 0 to t = 10 s the acceleration is also zero in this interval.digAnsr: b,c,dAns : (b) The acceleration at t = 0 may be zero.
(c) If the acceleration is zero from t = 0 s to t = 10 s, the speed is also zero in this interval.
(d) If the speed is zero from t = 0 s to t = 10 s, the acceleration is also zero in this interval.
(b) Acceleration will be zero only when the change in velocity is zero.
(c) Since the acceleration is zero from t = 0 s to t = 10 s, change in velocity is 0.
Velocity in this interval = Initial velocity = 0
Also,
Speed in this interval = Initial speed = 0
(d) From t = 0 s to t = 10 s, speed is zero.
Here, velocity is zero and initial velocity is zero.
So, the change in velocity is zero; i.e., acceleration is zero.
- Qstn #7Mark the correct statements:
-(a) The magnitude of the velocity of a particle is equal to its speed.
(b) The magnitude of average velocity in an interval is equal to its average speed in that interval.
(c) It is possible to have a situation in which the speed of a particle is always zero but the average speed is not zero.
(d) It is possible to have a situation in which the speed of the particle is never zero but the average speed in an interval is zero.digAnsr: aAns : (a) The magnitude of the velocity of a particle is equal to its speed.
(a) Velocity being a vector quantity has magnitude as well as direction, and magnitude of velocity is called speed.
(b) Average velocity = `` \frac{\,\mathrm{\,Total \,}\,\mathrm{\,displacement \,}}{\,\mathrm{\,Total \,}\,\mathrm{\,time \,}\,\mathrm{\,taken \,}}``
Average speed = `` \frac{\,\mathrm{\,Total \,}\,\mathrm{\,distance \,}\,\mathrm{\,travelled \,}}{\,\mathrm{\,Total \,}\,\mathrm{\,time \,}\,\mathrm{\,taken \,}}``
Distance`` \ge ``Displacement
∴ Average speed`` \ge ``Average velocity
The magnitude of average velocity in an interval is not always equal to its average speed in that interval.
(c) If speed is always zero, then the distance travelled is always zero. Hence, the total distance travelled and the average speed will be zero.
(d) If the speed of a particle is never zero, the distance travelled by the particle is never zero. Hence, the average speed will not be zero.
- Qstn #8The velocity-time plot for a particle moving on a straight line is shown in the figure.
Figure
--(a) The particle has a constant acceleration.
(b) The particle has never turned around.
(c) The particle has zero displacement.
(d) The average speed in the interval 0 to 10 s is the same as the average speed in the interval 10 s to 20 s.digAnsr: a,dAns : (a) The particle has a constant acceleration.
(d) The average speed in the interval 0 s to 10 s is the same as the average speed in the interval 10 s to 20 s.
Explanation:
(a) The slope of the v-t graph gives the acceleration. For the given graph, the slope is constant. So, acceleration is constant.
(b) From 0 to 10 seconds, velocity is in positive direction and then in negative direction. This means that the particle turns around at t = 10 s.
(c) Area in the v-t curve gives the distance travelled by the particle.
Distance travelled in positive direction`` \ne ``Distance travelled in negative direction
∴ Displacement`` \ne ``Zero
(d) The area of the v-t graph from t = 0 s to t = 10 s is the same as that from t = 10 s to t = 20 s. So, the distance covered is the same. Hence, the average speed is the same.
- Qstn #9In figure shows the position of a particle moving on the X-axis as a function of time.
-(a) The particle has come to rest 6 times.
(b) The maximum speed is at t = 6s.
(c) The velocity remains positive for t = 0 to t = 6s.
(d) The average velocity for the total period shown is negative.
FiguredigAnsr: aAns : (a) The particle has come to rest 6 times.
Explanation:
(a) The slope of the x-t graph gives the velocity. Here, 6 times the slope is zero. So, the particle has come to rest 6 times.
(b) As the slope is not maximum at t = 6 s, the maximum speed is not at t = 6 s.
(c) As the slope is not positive from t = 0 s to t = 6s, the velocity does not remain positive.
(d) Average velocity = `` \frac{\,\mathrm{\,Total \,}\,\mathrm{\,displacement \,}}{\,\mathrm{\,Total \,}\,\mathrm{\,time \,}\,\mathrm{\,taken \,}}=\frac{{x}_{\,\mathrm{\,final \,}}-{x}_{\,\mathrm{\,initial \,}}}{t}``
`` ``
For the shown time (t = 6 s), the displacement of the particle is positive. Therefore, the average velocity is positive.
- Qstn #10The accelerations of a particle as seen from two frames S1 and S2 have equal magnitude 4 m/s2.
--(a) The frames must be at rest with respect to each other.
(b) The frames may be moving with respect to each other.
(c) The acceleration of S2 with respect to S1 may either be zero of 8 m/s2.
(d) The acceleration of S2 with respect to S1 may be anything between zero and 8 m/s2.digAnsr: dAns : (d) The acceleration of S2 with respect to S1 may be anything between zero and 8 m/s2.
Explanation:
`` {\stackrel{\to }{a}}_{{s}_{2}{s}_{1}}={\stackrel{\to }{a}}_{{s}_{2}\,\mathrm{\,p \,}}+{\stackrel{\to }{a}}_{\,\mathrm{\,p \,}{s}_{1}}``
`` \left|{\stackrel{\to }{a}}_{{s}_{2}{s}_{1}}\right|=\sqrt{{4}^{2}+{4}^{2}+32\,\mathrm{\,cos \,}\left(\theta \right)}``
`` -1<\,\mathrm{\,cos \,}\left(\theta \right)<1``
`` ``
`` 0<{\stackrel{\to }{a}}_{{s}_{2}{s}_{1}}<8``
- #Section : D