02: Physics And Mathematics : Cbse-xi-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

CBSE-XI-Physics

02: Physics and Mathematics

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #5
The magnitude of the vector product of two vectors
A→and B→may be
.(a) greater than AB
(b) equal to AB
(c) less than AB
(d) equal to zero.
digAnsr: b,c,d
Ans : (b) equal to AB
(c) less than AB
(d) equal to zero.
The magnitude of the vector product of two vectors `` \left|\stackrel{\to }{A}\right|`` and `` \left|\stackrel{\to }{B}\right|`` may be less than or equal to AB, or equal to zero, but cannot be greater than AB.

#
Section : D
Page No 29:

Qstn #1
A vector
A→makes an angle of 20° and
B→makes an angle of 110° with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.
Ans :
From the above figure, we have:
Angle between `` \stackrel{\to }{\mathrm{A}}`` and `` \stackrel{\to }{\mathrm{B}}`` = 110° - 20° = 90°
`` \left|\stackrel{\to }{\mathrm{A}}\right|=3\mathrm{m}\mathrm{and}\left|\stackrel{\to }{\mathrm{B}}\right|=4\mathrm{m}``
Magnitude of the resultant vector is given by
`` \mathrm{R}=\sqrt{{\mathrm{A}}^{2}+{\mathrm{B}}^{2}+2\mathrm{AB}\mathrm{cos}\mathrm{\theta }}
=\sqrt{{3}^{2}+{4}^{2}+2\times 3\times 4\times \mathrm{cos}90°}
=5\mathrm{m}``
Let β be the angle between `` \stackrel{\to }{\mathrm{R}}\mathrm{and}\stackrel{\to }{\mathrm{A}}``.
`` \mathrm{\beta }={\mathrm{tan}}^{-1}\left(\frac{A\mathrm{sin}90°}{A+B\mathrm{cos}90°}\right)
={\mathrm{tan}}^{-1}\left(\frac{4\mathrm{sin}90°}{3+4\mathrm{cos}90°}\right)
={\mathrm{tan}}^{-1}\frac{4}{3}
={\mathrm{tan}}^{-1}\left(1.333\right)
=53°``
Now, angle made by the resultant vector with the X-axis = 53° + 20° = 73°
∴ The resultant `` \stackrel{\to }{\mathrm{R}}`` is 5 m and it makes an angle of 73° with the x-axis.
Page No 29:

Qstn #2
Let
A→andB→be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angle 30° and 60° respectively, find the resultant.
Ans : Angle between `` \stackrel{\to }{\mathrm{A}}\mathrm{and}\stackrel{\to }{\mathrm{B}}``, θ = 60° - 30° = 30°
`` \left|\stackrel{\to }{\mathrm{A}}\right|=\left|\stackrel{\to }{\mathrm{B}}\right|=10\mathrm{units}
\mathrm{The}\mathrm{magnitude}\mathrm{of}\mathrm{the}\mathrm{resultant}\mathrm{vector}\mathrm{is}\mathrm{given}\mathrm{by}
\mathrm{R}=\sqrt{{A}^{2}+{A}^{2}+2AA\mathrm{cos}\theta }
=\sqrt{{10}^{2}+{10}^{2}+2\times 10\times 10\times \mathrm{cos}30°}
=\sqrt{200+200\mathrm{cos}30°}
=\sqrt{200+200\times \frac{\sqrt{3}}{2}}
=19.3\mathrm{units}``

Let β be the angle between `` \stackrel{\to }{\mathrm{R}}\mathrm{and}\stackrel{\to }{\mathrm{A}}``.
`` \therefore \mathrm{\beta }={\mathrm{tan}}^{-1}\left(\frac{A\mathrm{sin}30°}{A+A\mathrm{cos}30°}\right)
\Rightarrow \mathrm{\beta }={\mathrm{tan}}^{-1}\left(\frac{10\mathrm{sin}30°}{10+10\mathrm{cos}30°}\right)
\Rightarrow \mathrm{\beta }={\mathrm{tan}}^{-1}\left(\frac{1}{2+\sqrt{3}}\right)={\mathrm{tan}}^{-1}\left(\frac{1}{3.372}\right)
\Rightarrow \mathrm{\beta }={\mathrm{tan}}^{-1}\left(0.26795\right)=15°``
Angle made by the resultant vector with the X-axis = 15° + 30° = 45°
∴ The magnitude of the resultant vector is 17.3 and it makes angle of 45° with the X-axis.
Page No 29:

Qstn #3
Add vectors
A→,B→andC→each having magnitude of 100 unit and inclined to the X-axis at angles 45°, 135° and 315° respectively.
Ans : First, we will find the components of the vector along the x-axis and y-axis. Then we will find the resultant x and y-components.
x-component of `` \stackrel{\to }{\mathrm{A}}=\mathrm{Acos}45°=100\mathrm{cos}45°=\frac{100}{\sqrt{2}}\mathrm{unit}``
x-component of `` \stackrel{\to }{\mathrm{B}}=\stackrel{\to }{\mathrm{B}}\mathrm{cos}135°=-\frac{100}{\sqrt{2}}``
x-component of `` \stackrel{\to }{\mathrm{C}}`` = `` \stackrel{\to }{\mathrm{C}}``cos315`` °`` = 100 cos 315°
`` =100\mathrm{cos}45°=\frac{100}{\sqrt{2}}``
Resultant x-component `` =\frac{100}{\sqrt{2}}-\frac{100}{\sqrt{2}}+\frac{100}{\sqrt{2}}=\frac{100}{\sqrt{2}}``

Now, y-component of `` \stackrel{\to }{\mathrm{A}}=100\mathrm{sin}45°=\frac{100}{\sqrt{2}}``
y-component of `` \stackrel{\to }{\mathrm{B}}=100\mathrm{sin}135°=\frac{100}{\sqrt{2}}``
y-component of `` \stackrel{\to }{\mathrm{C}}=100\mathrm{sin}315°=-\frac{100}{\sqrt{2}}``
Resultant y-component`` =\frac{100}{\sqrt{2}}+\frac{100}{\sqrt{2}}-\frac{100}{\sqrt{2}}=\frac{100}{\sqrt{2}}``
Magnitude of the resultant`` =\sqrt{{\left(\frac{100}{\sqrt{2}}\right)}^{2}+{\left(\frac{100}{\sqrt{2}}\right)}^{2}}``
`` =\sqrt{10000}=100``
Angle made by the resultant vector with the x-axis is given by
`` \mathrm{tan}\mathrm{\alpha }=\frac{y\mathrm{comp}}{x\mathrm{comp}}
=\frac{100\sqrt{2}}{100\sqrt{2}}=1``
⇒ α = tan^-1 (1) = 45°
∴ The magnitude of the resultant vector is 100 units and it makes an angle of 45° with the x-axis.
Page No 29:

Qstn #4
Let
a→=4i→+3j→andb→=3i→+4j→. (a) Find the magnitudes of (a)
a→, (b)
b→, (c)
a→+b→and(d)
a→-b→.
digAnsr: iv
Ans : Given: `` \stackrel{\to }{a}=4\stackrel{\to }{i}+3\stackrel{\to }{j}\mathrm{and}\stackrel{\to }{b}=3\stackrel{\to }{i}+4\stackrel{\to }{j}``
(a) Magnitude of `` \stackrel{\to }{a}`` is given by `` \left|\stackrel{\to }{a}\right|=\sqrt{{4}^{2}+{3}^{2}}=\sqrt{16+9}=5``
(b) Magnitude of `` \stackrel{\to }{b}`` is given by `` \left|\stackrel{\to }{b}\right|=\sqrt{{3}^{2}+{4}^{2}}=\sqrt{9+16}=5``
(c) `` \stackrel{\to }{a}+\stackrel{\to }{b}=(4\vec{i}+3\vec{j})+(3\vec{i}+4\vec{j})=(7\vec{i}+7\vec{j})``
∴ Magnitude of vector `` \stackrel{\to }{a}+\stackrel{\to }{b}`` is given by `` \left|\stackrel{\to }{a}+\stackrel{\to }{b}\right|=\sqrt{49+49}=\sqrt{98}=7\sqrt{2}``
(d) `` \stackrel{\to }{a}-\stackrel{\to }{b}=\left(4\stackrel{\to }{i}+3\stackrel{\to }{j}\right)-\left(3\stackrel{\to }{i}+4\stackrel{\to }{j}\right)=\stackrel{\to }{i}-\stackrel{\to }{j}``
∴ Magnitude of vector `` \stackrel{\to }{a}-\stackrel{\to }{b}`` is given by `` \left|\stackrel{\to }{a}-\stackrel{\to }{b}\right|=\sqrt{{\left(1\right)}^{2}+{\left(-1\right)}^{2}}=\sqrt{2}``
Page No 29:

Qstn #5
Refer to figure (2-E1). Find (a) the magnitude, (b) x and y component and (c) the angle with the X-axis of the resultant of
OA→,BC→andDE→.

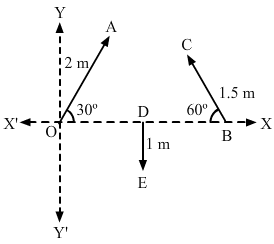
Figure (2-E1)
digAnsr: a
Ans : First, let us find the components of the vectors along the x and y-axes. Then we will find the resultant x and y-components.
x-component of `` \stackrel{\to }{\mathrm{OA}}=2\mathrm{cos}30°=\sqrt{3}`` m
x-component of `` \stackrel{\to }{\mathrm{BC}}`` =1.5cos120°
`` =-\frac{\left(1.5\right)}{2}=-7.5`` m
x-component of `` \stackrel{\to }{\mathrm{DE}}`` = 1cos270°
= 1 × 0 = 0 m
y-component of `` \stackrel{\to }{\mathrm{OA}}`` = 2 sin 30° = 1
y-component of `` \stackrel{\to }{\mathrm{BC}}`` = 1.5 sin 120°
`` =\frac{\left(\sqrt{3}\times 1.5\right)}{2}=1.3``
y-component of `` \stackrel{\to }{\mathrm{DE}}`` = 1 sin 270° = -1
x-component of resultant `` {\mathrm{R}}_{x}=\sqrt{3}-0.75+0=0.98\mathrm{m}``
y-component of resultant R_y = 1 + 1.3 - 1 = 1.3 m
`` \therefore \mathrm{Resultant},\mathrm{R}=\sqrt{{\left({R}_{x}\right)}^{2}+{\left({R}_{y}\right)}^{2}}
=\sqrt{{\left(0.98\right)}^{2}+{\left(1.3\right)}^{2}}
=\sqrt{0.96+1.69}
=\sqrt{2.65}
=1.6\mathrm{m}``
If it makes an angle α with the positive x-axis, then
`` \mathrm{tan}\mathrm{\alpha }=\frac{y-component}{x-\mathrm{component}}
=\frac{1.3}{0.98}=1.332``
∴ α = tan^-1 (1.32)
Page No 29:

Qstn #6
Two vectors have magnitudes 2 unit and 4 unit respectively. What should be the angle between them if the magnitude of the resultant is (a) 1 unit, (b) 5 unit and (c) 7 unit.
digAnsr: a
Ans : Let the two vectors be `` \stackrel{\to }{a}`` and `` \stackrel{\to }{b}``.
Now, `` \left|\stackrel{\to }{a}\right|=3\mathrm{and}\left|\stackrel{\to }{b}\right|=4``
(a) If the resultant vector is 1 unit, then
`` \sqrt{{\stackrel{\to }{a}}^{2}+{\stackrel{\to }{b}}^{2}+2.\stackrel{\to }{a}.\stackrel{\to }{b}\mathrm{cos}\mathrm{\theta }}=1
\Rightarrow \sqrt{{3}^{2}+{4}^{2}+2.3.4\mathrm{cos}\mathrm{\theta }}=1
``
Squaring both sides, we get:
`` 25+24\mathrm{cos}\mathrm{\theta }=1
\Rightarrow 24\mathrm{cos}\mathrm{\theta }=-24
\Rightarrow \mathrm{cos}\mathrm{\theta }=-1
\Rightarrow \mathrm{\theta }=180°``
Hence, the angle between them is 180°.
(b) If the resultant vector is 5 units, then
`` \sqrt{{\stackrel{\to }{a}}^{2}+{\stackrel{\to }{b}}^{2}+2.\stackrel{\to }{a}.\stackrel{\to }{b}\mathrm{cos}\mathrm{\theta }}=5
\Rightarrow \sqrt{{3}^{2}+{4}^{2}+2.3.4\mathrm{cos}\mathrm{\theta }}=5``
Squaring both sides, we get:
25 + 24 cos θ = 25
⇒ 24 cos θ = 0
⇒ cos θ = 90°
Hence, the angle between them is 90°.
(c) If the resultant vector is 7 units, then
`` \sqrt{{\stackrel{\to }{a}}^{2}+{\stackrel{\to }{b}}^{2}+2.\stackrel{\to }{a}.\stackrel{\to }{b}\mathrm{cos}\mathrm{\theta }}=1
\Rightarrow \sqrt{{3}^{2}+{4}^{2}+2.3.4\mathrm{cos}\mathrm{\theta }}=7``
Squaring both sides, we get:
25 + 24 cos θ = 49,
⇒ 24 cos θ = 24
⇒ cos θ = 1
⇒ θ = cos^-1 1 = 0°
Hence, the angle between them is 0°.
Page No 29:

Qstn #7
A spy report about a suspected car reads as follows. “The car moved 2.00 km towards east, made a perpendicular left turn, ran for 500 m, made a perpendicular right turn, ran for 4.00 km and stopped”. Find the displacement of the car.
Ans : The displacement of the car is represented by `` \stackrel{\to }{\mathrm{AD}}``.
`` \stackrel{\to }{\mathrm{AD}}=2\vec{i}+0.5\vec{j}+4\vec{i}
=6\vec{i}+0.5\vec{j}``
Magnitude of `` \stackrel{\to }{\mathrm{AD}}`` is given by
`` \mathrm{AD}=\sqrt{{\mathrm{AE}}^{2}+{\mathrm{DE}}^{2}}
=\sqrt{{6}^{2}+{\left(0.5\right)}^{2}}
=\sqrt{36+0.25}=6.02\mathrm{km}``

Now, `` \mathrm{tan}\mathrm{\theta }=\frac{\mathrm{DE}}{\mathrm{AE}}=\frac{1}{12}``
`` \Rightarrow \mathrm{\theta }={\mathrm{tan}}^{-1}\left(\frac{1}{12}\right)``
Hence, the displacement of the car is 6.02 km along the direction `` {\mathrm{tan}}^{-1}\left(\frac{1}{12}\right)`` with positive the x-axis.
Page No 29:

Qstn #8
A carrom board (4 ft × 4 ft square) has the queen at the centre. The queen, hit by the striker moves to the from edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen (a) from the centre to the front edge, (b) from the front edge to the hole and (c) from the centre to the hole.
Ans :
Consider that the queen is initially at point A as shown in the figure.
Let AB be x ft.
So, DE = (2 `` -`` x) ft
In ∆ABC, we have:
`` \mathrm{tan}\mathrm{\theta }=\frac{x}{2}`` ...(i)
Also, in ∆DCE, we have:
`` \mathrm{tan}\mathrm{\theta }=\frac{\left(2-x\right)}{4}`` ...(ii)
From (i) and (ii), we get:
`` \frac{x}{2}=\frac{\left(2-x\right)}{4}
\Rightarrow 2\left(2-x\right)=4x
\Rightarrow 4-2x=4x
\Rightarrow 6x=4
\Rightarrow x=\frac{2}{3}\mathrm{ft}``
(a) In ∆ABC, we have:
`` \mathrm{AC}=\sqrt{{\mathrm{AB}}^{2}+{\mathrm{BC}}^{2}}``
`` =\sqrt{{\left(\frac{2}{3}\right)}^{2}+{2}^{2}}
=\sqrt{\frac{4}{9}+4}=\sqrt{\frac{40}{9}}
=\frac{2}{3}\sqrt{10}\mathrm{ft}``
(b) In ∆CDE, we have:
DE`` =2-\frac{2}{3}=\frac{6-2}{3}=\frac{4}{3}\mathrm{ft}``
CD = 4 ft
`` \therefore \mathrm{CE}=\sqrt{{\mathrm{CD}}^{2}+{\mathrm{DE}}^{2}}
=\sqrt{{4}^{2}+{\left(\frac{4}{3}\right)}^{2}}
=\frac{4}{3}\sqrt{10}\mathrm{ft}``
(c) In ∆AGE, we have:
`` \mathrm{AE}=\sqrt{{\mathrm{AG}}^{2}+{\mathrm{GE}}^{2}}``
`` =\sqrt{{2}^{2}+{2}^{2}}
=\sqrt{8}+2\sqrt{2}\mathrm{ft}``
Page No 29:

Qstn #9
A mosquito net over a 7 ft × 4 ft bed is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net.
Ans : Displacement vector of the mosquito, `` \stackrel{\to }{r}=7\vec{i}+4\vec{i}+3\vec{k}``

#9-a
Find the magnitude of the displacement of the mosquito.
Ans : Magnitude of displacement`` =\sqrt{{7}^{2}+{4}^{2}+{3}^{2}}``
`` =\sqrt{74}\mathrm{ft}``

#9-b
Taking the hole as the origin, the length of the bed as the X-axis, it width as the Y-axis, and vertically up as the Z-axis, write the components of the displacement vector.
Ans : The components of the displacement vector are 7 ft, 4 ft and 3 ft along the X, Y and Z-axes, respectively.
Page No 29:

Qstn #10
Suppose
a→is a vector of magnitude 4.5 units due north. What is the vector (a)
3a→, (b)
-4a→?
digAnsr: iv
Ans : Given: `` \stackrel{\to }{a}`` is a vector of magnitude 4.5 units due north.
Case (a):
`` 3\left|\stackrel{\to }{a}\right|=3\times 4.5=13.5``
∴ `` 3\stackrel{\to }{a}`` is a vector of magnitude 13.5 units due north.
Case (b):
`` \left|-4\stackrel{\to }{a}\right|=4\times 1.5=6\mathrm{units}``
∴`` -4\stackrel{\to }{a}`` is a vector of magnitude 6 units due south.
Page No 29:

Qstn #11
Two vectors have magnitudes 2 m and 3m. The angle between them is 60°. Find
Ans : Let the two vectors be `` \left|\stackrel{\to }{a}\right|=2\mathrm{m}\mathrm{and}\left|\stackrel{\to }{b}\right|=3\mathrm{m}``.
Angle between the vectors, θ = 60°