Exercise 18





1. If A is an acute angle and sin A = 3/5, find all other trigonometric ratios of angle A (using trigonometric identities).



Answer




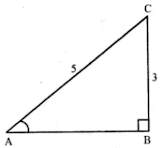
Given,

sin A = 3/5 and A is an acute angle

So, in ∆ABC we have ∠B = 90^o

And,

AC = 5 and BC = 3

By Pythagoras theorem,

AB = √(AC² - BC²)

= √(5² - 3²) = √(25 - 9)


=
√16

= 4

Now,

cos A = AB/AC = 4/5

tan A = BC/AB = 3/4

cot A = 1/tan θ = 4/3

sec A = 1/cos θ = 5/4

cosec A = 1/sin θ = 5/3




2.
If A is an acute angle and sec A = 17/8, find all other trigonometric ratios of angle A (using trigonometric identities).



Answer




Given,

sec A = 17/8 and A is an acute angle

So, in ∆ ABC we have ∠B = 90^o

And,

AC = 17 and AB = 8

By Pythagoras theorem,

BC = √(AC² - AB²)

= √(17² - 8²) = √(289 - 64)
=
√225

= 15

Now,

sin A = BC/AC = 15/17

cos A = 1/sec A = 8/17

tan A = BC/AB = 15/8

cot A = 1/tan A= 8/15

cosec A = 1/sin A = 17/15




3.
Express the ratios cos A, tan A and sec A in terms of sin A.



Answer

We know that,

sin² A + cos² A = 1

So,

cos A = √(1 - sin² A)

tan A = sin A/cos A = sin A/ √(1 - sin² A)

sec A = 1/cos A = 1/ (√1 - sin² A)




4.
If tan A = 1/√3, find all other trigonometric ratios of angle A.



Answer




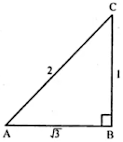
Given, tan A = 1/√3

In right ∆ ABC,

tan A = BC/AB = 1/√3

So,

BC = 1 and AB = √3

By Pythagoras theorem,

AC = √(AB² + BC²)

= √[(√3)² + (1)²]

= √(3 + 1)

= √4

= 2

Hence,

sin A = BC/AC = ½

cos A = AB/AC = √3/2

cot A = 1/tan A = √3

sec A = 1/cos A = 2/√3

cosec A = 1/sin A = 2/1 = 2




5.
If 12 cosec θ = 13, find the value of (2 sin θ - 3 cos θ)/(4 sin θ - 9 cos θ)



Answer

Given,

12 cosec θ = 13

⇒ cosec θ = 13/12

In right ∆ ABC,

∠A = θ

So,

cosec θ = AC/BC = 13/12

AC = 13 and BC = 12

By Pythagoras theorem,

AB = √(AC² - BC²)

= √[(13)² - (12)²]

= √(169 - 144)

= √25

= 5

Now,

sin θ = BC/AC = 12/13

cos θ = AB/AC = 5/13

Hence,

(2sin θ - 3cos θ)/(4sin θ - 9 cos θ)

= (2 × 12/13 - 3 × 5/13)/(4 × 12/13 - 9 × 5/13)

= (24/13 - 15/13)/(48/13 - 45/13)

= 9/13 ÷ 3/13

= 9/13 × 13/3

= 3





Without using trigonometric tables, evaluate the following (6 to 10):


6. (i) cos²26^o+ cos 64^o sin 26^o + (tan 36^o/cot 54^o)


(ii) (sec 17^o/ cosec 73^o) + (tan 68^o/ cot 22^o) + cos² 44^o + cos² 46^o



Answer

Given,

(i) cos² 26^o + cos 64^o sin 26^o + (tan 36^o/cot 54^o)

= cos² 26^o + cos (90^o - 16^o) sin 26^o + [tan 36^o/cot (90^o - 54^o)]

= [cos² 26^o + sin² 26^o] + (tan 36^o/tan 36^o)

= 1 + 1 = 2

(ii) (sec 17^o/cosec 73^o) + (tan 68^o/cot 22^o) + cos² 44^o + cos² 46^o

= [sec 17^o/cosec (90^o - 73^o)] + [(tan 90^o - 22^o)/cot 22^o] + cos² (90^o - 44^o) + cos² 46^o

= [sec 17^o/sec 17^o] + [cot 22^o/cot 22^o] + [sin² 46^o + cos² 46^o]

= 1 + 1 + 1

= 3




7.
(i) (sin 65^o/cos 25^o) + (cos 32^o/sin 58^o) - sin 28^osec 62^o+ cosec² 30^o


(ii) (sin 29^o/ cosec 61^o) + 2 cot 8° cot 17° cot 45° cot 73° cot 82° - 3(sin² 38° + sin² 52°).



Answer

Given,

(i) (sin 65^o/cos 25^o) + (cos 32^o/sin 58^o) - sin 28^o sec 62^o + cosec² 30^o

= (sin 65^o/cos (90^o - 65^o)) + (cos 32^o/sin (90^o - 32^o)) - sin 28^o sec (90^o - 28^o) + 2²

= (sin 65^o/sin 65^o)+ (cos 32^o/cos 32^o) - [sin 28^o x cosec 28^o] + 4

= 1 + 1 - 1 + 4

= 5

(ii) (sin 29^o/cosec 61^o) + 2 cot 8° cot 17° cot 45° cot 73° cot 82° - 3(sin² 38° + sin² 52°).

= (sin 29^o/cosec (90^o - 29^o)) + [2 cot 8° cot 17° cot 45° cot (90° - 17^o) cot (90^o - 8^o)] - 3(sin² 38° + sin² (90° - 38^o))

= (sin 29^o/sin 29^o) + [2 cot 8° cot 17° cot 45° tan 17^o tan 8^o] - 3(sin² 38° + cos² 38°)

= 1 + 2[(cot 8° tan 8^o) (cot 17° tan 17^o) cot 45°] - 3(1)

= 1 + 2[1×1×1] - 3

= 1 + 2 - 3

= 0




8.
(i) (sin 35^ocos 55^o+ cos 35^o sin 55 ^o)/ (cosec² 10^o - tan² 80 ^o)


(ii) sin² 34^o + sin² 56^o + 2 tan18^o tan 72^o - cot² 30^o



Answer

Given,

(i) (sin 35^o cos 55^o + cos 35^o sin 55^o)/ (cosec² 10^o - tan² 80^o)

= sin 35^o cos (90^o - 35^o) + cos 35^o sin (90^o - 35^o)/(cosec² 10^o - tan²(90^o - 10^o)

= sin 35^o sin 35^o + cos 35^o cos 35^o)/(cosec² 10^o - cot² 10^o)

= (sin² 35^o + cos² 35^o)/(cosec² 10^o - cot² 10^o)

= 1/1

= 1

(ii) sin² 34^o + sin² 56^o + 2 tan18^o tan 72^o - cot² 30^o

= sin² 34^o + sin² (90^o - 34^o) + 2 tan18^o tan (90^o - 18^o) - cot² 30^o

= [sin² 34^o + cos² 34^o] + 2 tan18^o cot 18^o - cot² 30^o

= 1 + 2 x 1 - (√3)²

= 1 + 2 - 3

= 0




9.
(i) (tan 25^o/cosec 65^o)²+ (cot 25^o/sec 65^o)²+ 2 tan 18^o tan 45^o tan 75^o


(ii) (cos² 25^o + cos² 65^o) + cosec θ sec (90^o - θ) - cot θ tan (90^o - θ)



Answer

Given,

(i) (tan 25^o/ cosec 65^o)² + (cot 25^o/ sec 65^o)² + 2 tan 18^o tan 45^o tan 75^o






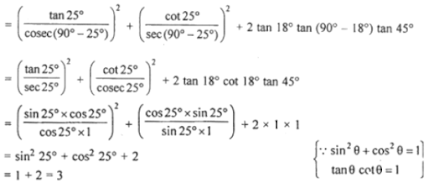
(ii) (cos² 25^o + cos² 65^o) + cosec θ sec (90^o - θ) - cot θ tan (90^o - θ)

= cos² 25^o + cos² (90^o - 25^o) + cosec θ sec (90^o - θ) - cot θ. cot θ

= (cos² 25^o + sin² 25^o) + (cosec² θ - cot² θ)

= 1 + 1 = 2




10.
(i) 2(sec² 35° - cot² 55°) - (cos 28°cosec 62°)/(tan18° tan36° tan30° tan30° tan54° tan72°)


(ii) cosec² (90 - θ) - tan² θ)/(2(cos²48° + cos²42°) - (2tan²30° sec²52° sin²38°)/(cosec²70° - tan²20°)



Answer

(i) 2(sec² 35° - cot² 55°) = (cos28° cosec62°)/(tan18° tan36° tan30° tan54° tan72°)


(ii)




11. Prove that following:


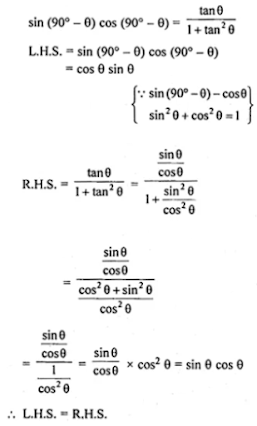
(i) cos θ sin (90° - θ) + sin θ cos (90° - θ) = 1


(ii) tan θ/tan (90^o - θ) + sin (90^o - θ)/cos θ = sec² θ


(iii) (cos (90^o - θ) cos θ)/tan θ + cos² (90^o - θ) = 1


(iv) sin (90^o - θ) cos (90^o - θ) = tan θ/ (1 + tan² θ)



Answer

(i) L.H.S. = cos θ sin (90° - θ) + sin θ cos (90° - θ)

= cos θ x cos θ + sin θ x sin θ

= cos² θ + sin² θ

= 1 = R.H.S.

(ii) L.H.S = tan θ/tan (90^o - θ) + sin (90^o - θ)/cos θ

= tan θ/ cot θ + cos θ/ cos θ

= tan θ/ (1/tan θ) + 1

= tan² θ + 1 = sec² θ = R.H.S.

(iii) L.H.S. = (cos (90^o - θ) cos θ)/tan θ + cos² (90^o - θ)

= (sin θ cos θ)/tan θ + sin² θ

= (sin θ cos θ)/(sin θ/cos θ) + sin² θ

= cos² θ + sin² θ
= 1 = R.H.S.

(iv)








Prove that following (12 to 30) identities, where the angles involved are acute angles for which the trigonometric ratios as defined:


12. (i) (sec A + tan A) (1 - sin A) = cos A


(ii) (1 + tan² A) (1 - sin A) (1 + sin A) = 1.



Answer

Given,

(i) (sec A + tan A)(1 - sin A) = cos A

L.H.S. = (sec A + tan A)(1 - sin A)


(ii)



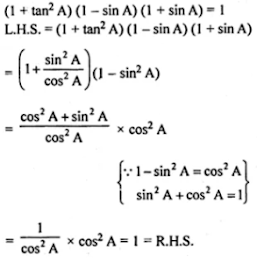
13.
(i) tan A + cot A = sec A cosec A


(ii) (1 - cos A) (1 + sec A) = tan A sin A.



Answer

(i) L.H.S. = tan A + cot A

= sin A/cos A + cos A/sin A

= (sin² A + cos² A)/(sin A cos A)

= 1/(sin A cos A)

= sec A cosec A

= R.H.S

(ii) L.H.S. = (1 - cos A) (1 + sec A)

= (1 - cos A)(1 + 1/cos A)

= (1 - cos A)(cos A + 1)/cos A

= (1 - cos² A)/(cos A)

= (sin²A)/(cos A)

= sin² A/cos A

= sin A × sin A/cos A {1 - cos² A = sin² A}

= tan A sin A

= R.H.S.





14.
(i) 1/(1 + cos A) + 1/(1 - cos A) = 2cosec²A


(ii) (1/sec A + tan A) + (1/sec A - tan A) = 2 sec A



Answer

(i) 1/(1 + cos A) + 1/(1 - cos A) = 2cosec² A

L.H.S. = 1/(1 + cos A) + 1/(1 - cos A)


(ii)





15.
(i) sin A/ (1 + cos A) = (1 - cos A)/ sin A


(ii) (1 - tan² A)/ (cot² A - 1) = tan² A


(iii) sin A/ (1 + cos A) = cosec A - cot A



Answer

(i) L.H.S. = sin A/(1 + cos A)

On multiplying and dividing by (1 - cos A), we have


(ii)


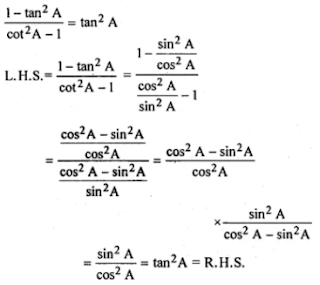
(iii)



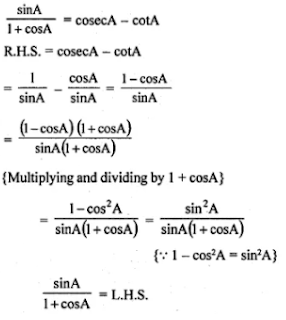
16.
(i) (sec A - 1)/(sec A + 1) = (1 - cos A)/(1 + cos A)


(ii) tan² θ/ (sec θ - 1)² = (1 + cos θ)/ (1 - cos θ)


(iii) (1 + tan A)² + (1 - tan A)² = 2 sec² A


(iv) sec² A + cosec² A = sec² A. cosec² A



Answer

(i) (sec A - 1)/(sec A + 1) = (1 - cos A)/(1 + cos A)

L.H.S. = (sec A - 1)/(sec A + 1)


(ii)


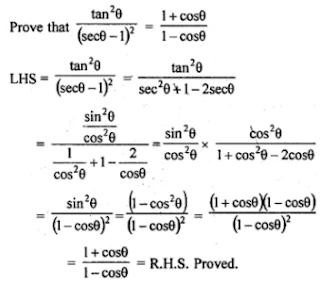
(iii) L.H.S. = (1 + tan A)² + (1 - tan A)²= 1 + 2 tan A + tan² A + 1 - 2 tan A + tan² A

= 2 + 2 tan² A

= 2(1 + tan² A) [As 1 + tan² A = sec² A]

= 2 sec² A

= R.H.S.

(iv) L.H.S = sec² A + cosec² A

= 1/cos² A + 1/sin² A

= (sin² A + cos² A)/(sin² A cos² A)

= 1/ (sin² A cos² A)

= sec² A cosec² A = R.H.S




17.
(i) (1 + sin A)/cos A + cos A/(1 + sin A) = 2 sec A


(ii) tan A/(sec A - 1) + tan A/(sec A + 1) = 2cosec A



Answer

(i) L.H.S. = (1 + sin A)/cos A + cos A/(1 + sin A)


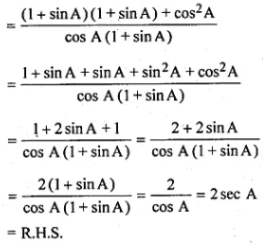
(ii)



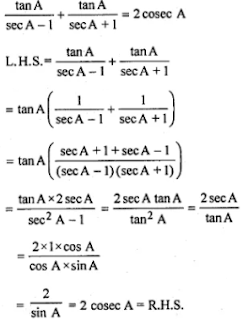
18.
(i) cosec A/(cosec A - 1) + cosec A/(cosec A + 1) = 2 sec²A


(ii) cot A - tan A = (2cos² A - 1)/ (sin A - cos A)


(iii) (cot A - 1)/ (2 - sec² A) = cot A/ (1 + tan A)



Answer

(i) L.H.S. = cosec A/(cosec A - 1) + cosec A/(cosec A + 1)


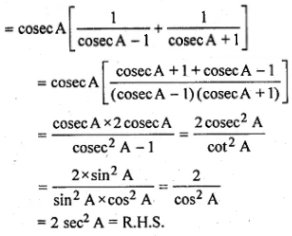
(ii)

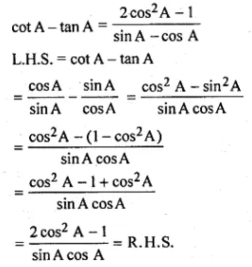
(iii)


19.
(i) tan²θ - sin²θ = tan² θ sin² θ
(ii) cos θ/ (1 - tan θ) - sin² θ/ (cos θ - sin θ) = cos θ + sin θ



Answer

(i) L.H.S = tan² θ - sin² θ



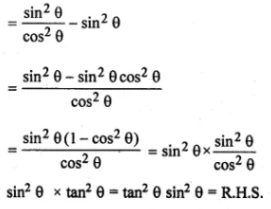
(ii)


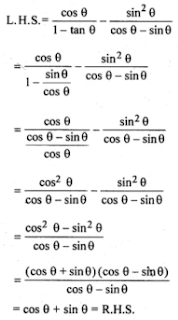
20. (i) cosec⁴θ - cosec²θ = cot⁴ θ + cot² θ
(ii) 2 sec² θ - sec⁴ θ - 2 cosec² θ + cosec⁴ θ = cot⁴ θ - tan⁴ θ.
Answer
(i) L.H.S. = cosec⁴ θ - cosec² θ
= cosec² θ (cosec² θ - 1)
= cosec² θ cot² θ [cosec² θ - 1 = cot² θ]
= (cot² θ + 1) cot² θ
= cot⁴ θ + cot² θ
= R.H.S.
(ii) L.H.S. = 2 sec² θ - sec⁴ θ - 2 cosec² θ + cosec⁴ θ
= 2 (tan² θ + 1) - (tan² θ + 1)² - 2 (1 + cot² θ) + (1 + cot² θ)²
{∵ sec² θ = tan² θ + 1 cosec² θ = 1 + cot² θ}
= 2 tan² θ + 2 - (tan⁴ θ + 2 tan² θ + 1) - 2 - 2 cot² θ + (1 + 2 cot² θ + cot⁴ θ)
= 2 tan² θ + 2 - tan⁴ θ - 2 tan² θ - 1 - 2 - 2 cot² θ + 1 + 2 cot² θ + cot⁴ θ
= cot⁴ θ - tan⁴ θ = R.H.S.
21. (i) (1 + cos θ - sin² θ)/(sin θ(1 + cos θ) = cot θ
(ii) (tan³ θ - 1)/(tan θ - 1) = sec² θ + tan θ
Answer
(i)
(1 + cos θ - sin² θ)/(sin θ(1 + cos θ) = cot θ


(ii)




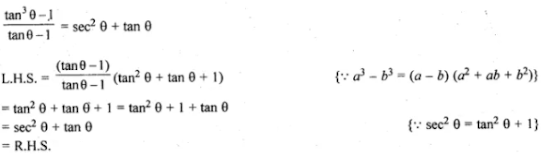
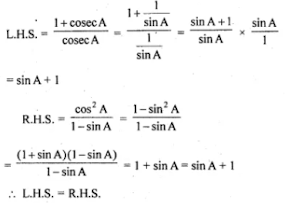
22. (i) (1 + cosec A)/cosec A = cos² A/(1 - sin A)
(ii)


= sin A/(1 + cos A)
Answer :
(i) (1 + cosec A)/cosec A = cos² A/(1 - sin A)
L.H.S. = (1 + cosec A)/cosec A



(ii)




23. (i)

= tan A + sec A
(ii)


= cosec A - cot A
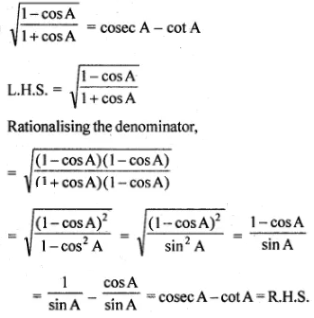
Answer
(i)


(ii)






24. (i)


= 2 cosec A
(ii) cos A cot A/(1 - sin A) = 1 + cosec A
Answer


(i)





(ii)
(cos A cot A)/(1 - sin A) = 1 + cosec A




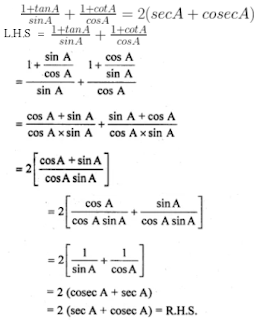
25. (i) (1 + tan A)/(sin A) + (1 + cot A)/cos A = 2(sec A + cosec A)
(ii) sec⁴ A - tan⁴ A = 1 + 2 tan² A
Answer

(i)


(ii)




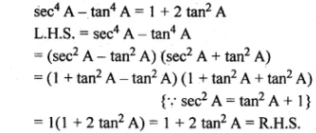
26. (i) cosec⁶ A - cot⁶ A = 3 cot² A cosec² A + 1
(ii) sec⁶ A - tan⁶ A = 1 + 3 tan² A + 3 tan⁴ A
Answer
(i) cosec⁶ A - cot⁶ A = 3 cot² A cosec² A + 1


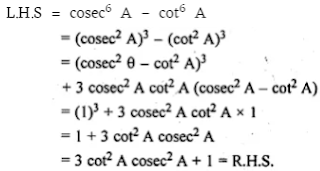
(ii)




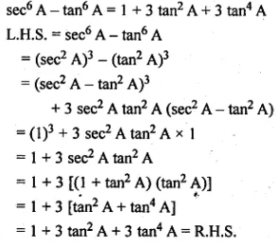
27. (i) (cot
θ
- cosec
θ - 1)/(cot θ - cosec θ + 1) = (1 + cos θ)/sin θ
(ii) sin θ/(cot θ + cosec θ) = 2 + sin θ/(cot θ - cosec θ)
Answer
(i) (cot θ - cosec θ - 1)/(cot θ - cosec θ + 1) = (1 + cos θ)/sin θ
L.H.S. = (cot θ - cosec θ - 1)/(cot θ - cosec θ + 1)


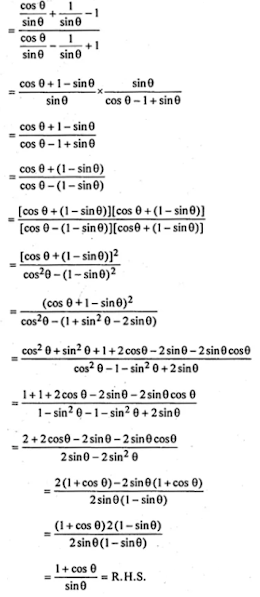
(ii)




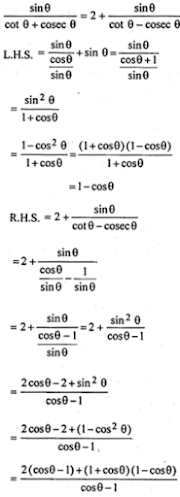
28. (i) (sin θ + cos θ) (sec θ + cosec θ) = 2 + sec θ cosec θ
(ii) (cosec A - sin A) (sec A - cos A) sec²A = tan A
Answer
(i) (sin θ + cos θ) (sec θ + cosec θ) = 2 + sec θ cosec θ
L.H.S. = (sin θ + cos θ) (sec θ + cosec θ)


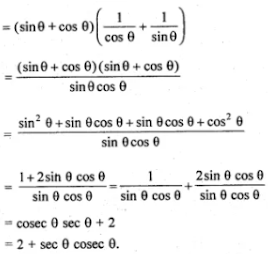
(ii)


dlt25477130978406478026">


29. (i) (sin³ A + cos³ A)/(sin A + cos A) + (sin³ A - cos³ A)/(sin A - cos A) = 2
(ii) tan² A/(1 + tan² A) + cot² A/(1 + cot² A) = 1
Answer
(i) (sin³ A + cos³ A)/(sin A + cos A) + (sin³ A - cos³ A)/(sin A - cos A) = 2
L.H.S. = (sin³ A + cos³ A)/(sin A + cos A) + (sin³ A - cos³ A)/(sin A - cos A)



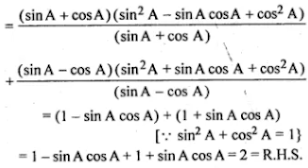
(ii) tan² A/(1 + tan² A) + cot² A/(1 + cot² A) = 1




30. (i) 1/ (sec A + tan A) - 1/cos A = 1/cos A - 1/(sec A - tan A)


(ii) (sin A + sec A)² + (cos A + cosec A)² = (1 + sec A cosec A)²


(iii) (tan A + sin A)/ (tan A - sin A) = (sec A + 1)/ (sec A - 1)



Answer

(i)
L.H.S. = 1/(sec A + tan A) - 1/cos A


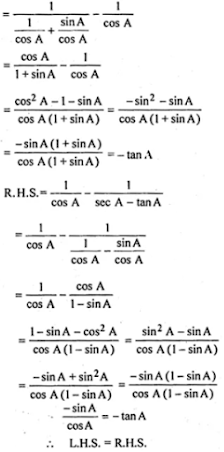
(ii)


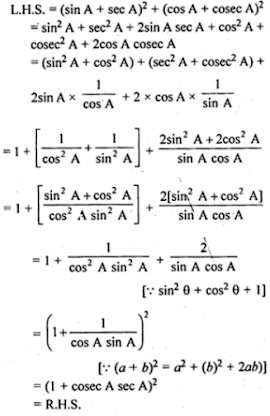
(iii) (tan A + sin A)/(tan A - sin A) = (sec A + 1)/(sec A - 1)









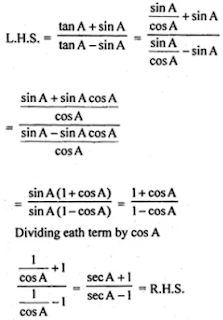
31. If sin θ + cos θ = √2 sin (90° - θ), show that cot θ = √2 + 1



Answer

Given, sin θ + cos θ = √2 sin (90° - θ)

sin θ + cos θ = √2 cos θ

On dividing by sin θ, we have




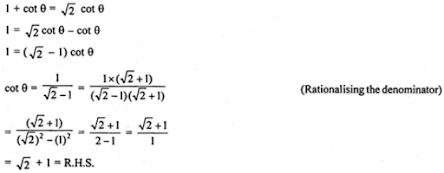
32. If 7 sin²θ + 3 cos²θ = 4, 0° ≤ θ ≤ 90°, then find the value of θ.



Answer

Given,

7 sin² θ + 3 cos² θ = 4, 0° ≤ θ ≤ 90°

⇒ 3 sin² θ + 3 cos² θ + 4 sin² θ = 4

⇒ 3 (sin² θ + 3 cos² θ) + 4 sin² θ = 4

⇒ 3 (1) + 4 sin² θ = 4

⇒ 4 sin² θ = 4 - 3

⇒ sin² θ = ¼

Taking square-root on both sides, we get

sin θ = ½

Thus, θ = 30^o





33. If sec θ + tan θ = m and sec θ - tan θ = n, prove that mn = 1.



Answer

Given,

sec θ + tan θ = m

sec θ - tan θ = n

Now,

mn = (sec θ + tan θ) (sec θ - tan θ)

= sec² θ - tan² θ = 1

Thus, mn = 1





34. If x - a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x²- y²= a² - b².



Answer

Given,

x = a sec θ + b tan θ,

y = a tan θ + b sec θ

Now,

x² - y² = (a sec θ + b tan θ)² - (a tan θ + b sec θ)²

= a² sec²θ + b² tan²θ + 2ab secθ tanθ - (a² tan²θ + b²sec²θ + 2ab secθ tanθ)
= a² sec²θ + b²tan²θ + 2ab secθ tanθ - a²tan²θ - b²sec²θ - 2ab secθ tanθ
= a² (sec²θ - tan²θ) - b² (sec²θ - tan²θ)
= a² × 1 - b² × 1 (sec²θ - tan²θ = 1)
= a² - b²






35. If x = h + a cos θ and y = k + a sin θ, prove that (x - h)²+ (y - k)²= a².



Answer

Given,

x = h + a cos θ

y = k + a sin θ

Now,

x - h = a cos θ

y - k = a sin θ

On squaring and adding we get

(x - h)² + (y - k)² = a² cos² θ + a² sin² θ

= a² (sin² θ + cos² θ)

= a² (1) [Since, sin² θ + cos² θ = 1]
Hence, proved





Chapter Test
1. (i) If θ is an acute angle and cosec θ = √5, find the value of cot θ - cos θ.
(ii) If θ is an acute angle and tan θ = 8/15, find the value of sec θ + cosec θ.
Answer
Given, θ is an acute angle and cosec θ = √5
So,
sin θ = 1/√5
And, cos θ = √(1 - sin² θ)
cos θ = √(1 - (1/√5)²)
= √(1 - (1/5))
= √(4/5)
cos θ = 2/√5
Now, cot θ - cos θ = (cos θ/sin θ) - cos θ


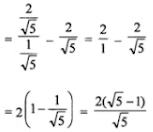
(ii) Given, θ is an acute angle and tan θ = 8/15
In fig. we have
tan θ = BC/AB = 8/15
So, BC = 8 and AB = 15
By Pythagoras theorem, we have
AC = √(AB² + BC²) = √(5² + 8²) = √(25 + 64) = √289
⇒ AC = 17
Now,
sec θ = AC/AB = 17/15
cosec θ = AC/BC = 17/8
So,
sec θ + cosec θ = 17/15 + 17/8
= (136 + 255)/ 120
= 391/120
= 3.31/120





2. Evaluate the following:
(i) 2
× (cos² 20° cos² 70°)/(sin² 25° + sin² 65°) - tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°
(ii) (sin²22° + sin²68°)/(cos²22° + cos²68°) + sin²63° + cos63° sin27°
Answer
(i) 2 × (cos² 20° cos² 70°)/(sin² 25° + sin² 65°) - tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°


(ii)






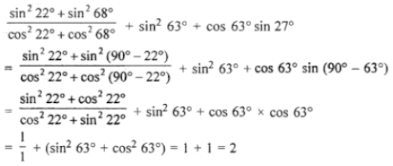
3. If 4/3 (sec²59^o- cot² 31^o) - 2/3 sin 90^o + 3 tan² 56^o tan² 34^o = x/2, then find the value of x.
Answer
Given,
4/3 (sec² 59^o - cot² 31^o) - 2/3 sin 90^o + 3 tan² 56^o tan² 34^o = x/2









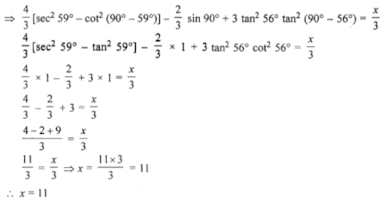
4.
(i) cos A/(1 - sin A) + cos A/(1 + sin A) = 2 sec A
(ii) cos A/(cosec A + 1) + cos A/(cosec A - 1) = 2 tan A
Answer
(i) cos A/(1 - sin A) + cos A/(1 + sin A) = 2 sec A


(ii)







5. (i) (cos θ - sin θ)(1 + tan θ)/2 cos² θ - 1 = sec θ
(ii) (cosec θ - sin θ) (sec θ - cos θ) (tan θ + cot θ) = 1.
Answer
(i) (cos θ - sin θ)(1 + tan θ)/2cos² θ - 1 = sec θ


(ii)





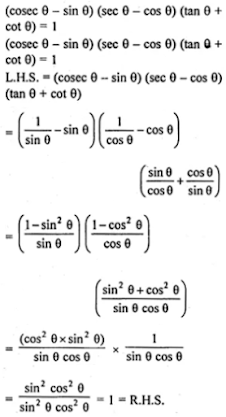
6. (i) sin²θ + cos⁴θ = cos² θ + sin⁴ θ
(ii) cot θ/(cosec θ + 1) + (cosec θ + 1)/cot θ = 2 sec θ



Answer
Given,
(i) L.H.S. = sin² θ + cos⁴ θ = cos² θ + sin⁴ θ
L.H.S. = sin² θ + cos⁴ θ
= (1 - cos² θ) + cos⁴ θ
= cos⁴ θ - cos² θ + 1
= cos² θ (cos² θ - 1) + 1
= cos² θ (- sin² θ) + 1
= 1 - sin² θ cos² θ
Now,
R.H.S. = cos² θ + sin⁴ θ
= (1 - sin² θ) + sin⁴ θ
= sin⁴ θ - sin² θ + 1
= sin² θ (sin² θ - 1) + 1
= sin² θ (-cos² θ) + 1
= 1 - sin² θ cos² θ
Hence, L.H.S. = R.H.S.
(ii)






7. (i) sec⁴A (1 - sin⁴A) - 2 tan² A = 1
(ii) 1/(sin A + cos A + 1) + 1/(sin A + cos A - 1)
= sec A + cosec A
Answer
(i) sec⁴ A (1 - sin⁴ A) - 2 tan² A = 1
L.H.S. = sec⁴ A (1 - sin⁴ A) - 2 tan² A
= 1/cos⁴ A (1 + sin² A)(1 - sin² A) - 2 tan² A
[∵ a² - b² = (a + b)(a - b)]


(ii)






8. (i) (sin³ θ + cos³ θ)/sin θ cos θ + sin θ cos θ = 1
(ii) (sec A - tan A)² (1 + sin A) = 1 - sin A.



Answer
(i) (sin³ θ + cos³ θ)/sinθ cosθ + sinθ cosθ = 1



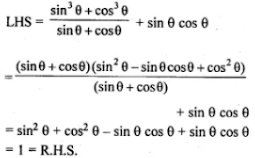
(ii)


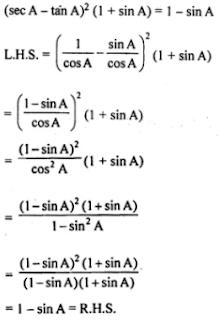
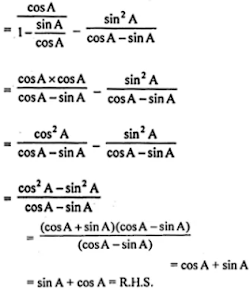
9. (i) cos A/(1 - tan A) - sin² A/(cos A - sin A)= sin A + cos A
(ii) (sec A - cosec A) (1 + tan A + cot A) = tan A sec A - cot A cosec A
(iii) tan² θ/(tan² θ - 1) - cosec² θ/(sec² θ - cosec² θ) = 1/(sin² θ - cos² θ)
Answer
(i) cos A/(1 - tan A) - sin² A/(cos A - sin A) = sin A + cos A
L.H.S. = cos A/(1 - tan A) - sin² A/(cos A - sin A)


(ii)



(iii)







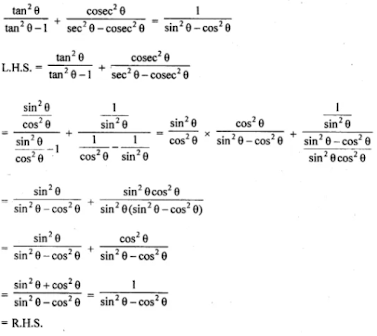
10. (sin A + cos A)/(sin A - cos A) + (sin A - cos A)/(sin A + cos A) = 2/(sin²A - cos² A = 2/(1 - 2 cos² A) = 2 sec² A/(tan² A - 1)
Answer
(sin A + cos A)/(sin A - cos A) + (sin A - cos A)/(sin A + cos A) = 2/(sin²A - cos² A = 2/(1 - 2 cos² A) = 2 sec² A/(tan² A - 1)
L.H.S. = (sin A + cos A)/(sin A - cos A) + (sin A - cos A)/(sin A + cos A)



11.
2 (sin⁶θ + cos⁶θ) - 3 (sin⁴ θ + cos⁴ θ) + 1 = 0



Answer
Given,
2 (sin⁶ θ + cos⁶ θ) - 3 (sin⁴ θ + cos⁴ θ) + 1 = 0
L.H.S. = 2 (sin⁶ θ + cos⁶ θ) - 3 (sin⁴ θ + cos⁴ θ) + 1
= 2 [(sin² θ)³ + (cos² θ)³] - 3 (sin⁴ θ + cos⁴ θ) + 1
= 2 [(sin² θ + cos² θ) (sin⁴ θ + cos⁴ θ - sin² θ cos² θ)] - 3 (sin⁴ θ + cos⁴ θ) + 1
= 2 (sin⁴ θ + cos⁴ θ - sin² θ cos² θ) - 3 (sin⁴ θ + cos⁴ θ) + 1
= 2 sin⁴ θ + 2 cos⁴ θ - 2 sin² θ cos² θ - 3 sin⁴ θ - 3 cos⁴ θ + 1
= 1 - sin⁴ θ - cos⁴ θ - 2 sin² θ cos² θ
= 1 - [sin⁴ θ + cos⁴ θ + 2 sin² θ cos² θ]
= 1 - 1
= 0 = R.H.S.




12.
If cot θ + cos θ = m, cot θ - cos θ = n, then prove that (m²- n²)²= 16.
Answer
Given,
cot θ + cos θ = m ...(i)
cot θ - cos θ = n ...(ii)
Adding (i) and (ii), we get



13.
If sec θ + tan θ = p, prove that sin θ = (p²- 1)/(p²+ 1)
Answer
Given, sec θ + tan θ = p
Prove that sin θ = (p² - 1)/(p² + 1)



14.
If tan A = n tan B and sin A = m sin B, prove that cos²A = (m²- 1)/ (n² - 1)
Answer
Given,
tan A = n tan B and sin A = m sin B
n = tan A/ tan B
m = sin A/ sin B



15.
If sec A = x + 1/4x, then prove that sec A + tan A = 2x or 1/2x
Answer
Given, sec A = x + 1/4x
We know that,



16.
When 0° < θ < 90°, solve the following equations:
(i) 2 cos² θ + sin θ - 2 = 0
(ii) 3 cos θ = 2 sin² θ
(iii) sec² θ - 2 tan θ = 0
(iv) tan² θ = 3 (sec θ - 1).
Answer
Given, 0° < θ < 90°
(i) 2 cos² θ + sin θ - 2 = 0
⇒ 2 (1 - sin² θ) + sin θ - 2 = 0
⇒ 2 - 2 sin² θ + sin θ - 2 = 0
⇒ -2 sin² θ + sin θ = 0
⇒ sin θ (1 - 2 sin θ) = 0
So, either sin θ = 0 or 1 - 2 sin θ = 0
If sin θ = 0
⇒ θ = 0^o
And, if 1 - 2 sin θ = 0
sin θ = ½
⇒ θ = 30^o
Thus, θ = 0^o or 30^o
(ii) 3 cos θ = 2 sin² θ
⇒ 3 cos θ = 2 (1 - cos² θ)
⇒ 3 cos θ = 2 - 2 cos² θ
⇒ 2 cos² θ + 3 cos θ - 2 = 0
⇒ 2 cos² θ + 4 cos θ - cos θ - 2 = 0
⇒ 2 cos θ (cos θ + 2) - 1(cos θ + 2) = 0
⇒ (2 cos θ - 1) (cos θ + 2) = 0
So, either 2 cos θ - 1 = 0 or cos θ + 2 = 0
If 2 cos θ - 1 = 0
cos θ = ½
⇒ θ = 60^o
And, for cos θ + 2 = 0
⇒ cos θ = -2 which is not possible being out of range.
Thus, θ = 60^o
(iii) sec² θ - 2 tan θ = 0
⇒ (1 + tan² θ) - 2 tan θ = 0
⇒ tan² θ - 2 tan θ + 1 = 0
⇒ (tan θ - 1)² = 0
⇒ tan θ - 1 = 0
⇒ tan θ = 1
Thus, θ = 45^o
(iv) tan² θ = 3 (sec θ - 1)
⇒ (sec² θ - 1) = 3 sec θ - 3
⇒ sec² θ - 1 - 3 sec θ + 3 = 0
⇒ sec² θ - 3 sec θ + 2 = 0
⇒ sec² θ - 2 sec θ - sec θ + 2 = 0
⇒ sec θ (sec θ - 2) - 1 (sec θ = 2) = 0
⇒ (sec θ - 1) (sec θ - 2) = 0
So, either sec θ - 1 = 0 or sec θ - 2 = 0
If sec θ - 1 = 0
sec θ = 1
⇒ θ = 0^o
And, if sec θ - 2 = 0
sec θ = 2
⇒ θ = 60^o
Thus, θ = 0^o or 60^o





Multiple Choice Questions
Choose the correct answer from the given four options (1 to 12)
1. cot² θ - 1/sin² θ is equal to
(a) 1
(b) -1
(c) sin² θ
(d) sec² θ
Answer
(b) -1

cot² θ - 1/sin² θ
= cos² θ/sin² θ - 1/sin² θ
= (cos² θ - 1)/sin² θ
= - sin² θ/sin² θ
= - 1
2. (sec² θ - 1)(1 - cosec² θ) is equal to
(a) -1
(b) 1
(c) 0
(d) 2
Answer
(a) -1

(sec² θ - 1)(1 - cosec² θ)
= (1/cos² θ - 1)(1 - 1/sin² θ)
= (1 - cos² θ)/cos² θ × (sin² θ - 1)/sin² θ
= (- sin² θ cos² θ)/(sin² θ cos² θ) = - 1
(∵ sin² θ + cos² θ = 1)
3. tan² θ/(1 + tan² θ) is equal to
(a) 2 sin² θ
(b) 2 cos² θ
(c) sin² θ
(d) cos² θ
Answer
(c) sin² θ

tan² θ/(1 + tan² θ)
tan² θ/(1 + tan² θ) = (sin² θ/cos² θ)/(1 + sin² θ/cos² θ)
= (sin² θ/cos² θ)/(cos² θ + sin² θ)/cos² θ
= (sin² θ/cos² θ) × cos² θ/(sin² θ + cos² θ)
(∵ sin² θ + cos² θ = 1)
= sin² θ/1
= sin² θ
4. (cos θ + sin θ)² + (cos θ - sin θ)² is equal to
(a) -2
(b) 0
(c) 1
(d) 2
Answer
(d) 2

(cos θ + sin θ)² + (cos θ - sin θ)²
= cos² θ + sin² θ + 2 sin θ cos θ + cos² θ + sin² θ - 2 sin θ cos θ
= 2(sin² θ + cos² θ)
= 2 × 1
= 2
(∵ sin² θ + cos² θ = 1)
5. (sec A + tan A)(1 - sin A) is equal to
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
Answer


(d) cos A

(sec A + tan A)(1 - sin A)
= (1/cos A + sin A/cos A) (1 - sin A)
= (1 + sin A)/cos A × 1 - sin A
= {(1 + sin A)(1 - sin A)}/cos A
= (1 - sin² A)/cos A
= cos² A/cos A
= cos A
6. (1 + tan² A)/(1 + cot² A) is equal to
(a) sec² A
(b) -1
(c) cot² A
(d) tan² A
Answer
(d) tan² A

(1 + tan² A)/(1 + cot² A)
(1 + tan² A)/(1 + cot² A) = (1 + sin² A/cos² A)/(1 + cos² A/sin² A)
= {(cos² A + sin² A)/cos² A}/(sin² A + cos² A)/sin² A}

= (1/cos² A)/(1/sin² A)
= 1/cos² A × sin² A/1
= sin² A/cos² A
= tan² A
7. If sec θ - tan θ = k, then the value of sec θ + tan θ is
(a) 1 - 1/k
(b) 1 - k
(c) 1 + k
(d) 1/k
Answer
(d) 1/k

sec θ - tan θ = k
1/cos θ - sin θ/cos θ = k
(1 - sin θ)/cos θ = k
Squaring both sides, we get
(1 - sin θ)/cos θ = k
Squaring both sides, we get
{(1 - sin θ)/cos θ}² = (k)²
⇒ (1 - sin θ)²/cos² θ = k²
= (1 - sin θ)²/(1 - sin² θ)
= k²
⇒ (1 - sin θ)²/(1 + sin θ)(1 - sin θ) = k²
= (1 - sin θ)/(1 + sin θ)

= k²

⇒ (1 + sin θ)/(1 - sin θ) = 1/k²

(1 + sin θ)/cos θ = 1/k
= 1/cos θ + sin θ/cos θ
= 1/k
⇒ sec θ + tan θ = 1/k
8. Which of the following is true for all values of θ (0° < θ < 90°) :
(a) cos² θ - sin² θ = 1
(b) cosec² θ - sec² θ = 1
(c) sec² θ - tan² θ = 1
(d) cot² θ - tan² θ = 1
Answer
(c) sec² θ - tan² θ = 1

∴ sec² θ - tan² θ = 1 is true for all values of θ as it is an identity.
(0° < θ < 90°)
9. If θ is an acute angle of a right triangle, then the value of sin θ cos (90° - θ) + cos θ sin (90° - θ) is
(a) 0
(b) 2 sin
θ cos θ
(c) 1
(d) 2 sin² θ
Answer
(c) 1

sin θ cos (90° - θ) + cos θ sin (90° - θ)
= sin θ sin θ + cos θ cos θ
{∵ sin(90° - θ) = cos θ, cos (90° - θ) = sin θ}
= sin² θ + cos² θ
= 1
10. The value of cos 65° sin 25° + sin 65° cos 25° is
(a) 0
(b) 1
(c) 2
(d) 4
Answer
(b) 1

cos 65° sin 25° + sin 65°cos 25°
= cos (90° - 25°) sin 25° + sin (90° - 25°) cos 25°
= sin 25°. sin 25° + cos 25°. cos 25°
∴ sin² 25° + cos² 25°
(∵ sin² θ + cos² θ = 1)
= 1





11. The value of 3 tan² 26° - 3 cosec² 64° is



(a) 0



(b) 3



(c) -3



(d) -1



Answer


(c) -3

3 tan² 26° - 3 cosec² 64°

= 3 tan² 26° - 3 cosec (90° - 26°)

= 3 tan² 26° - 3 sec² 26°

= 3(tan² 26° - sec² 26°) {∵ sec² θ - tan² θ = 1}

= 3 × (-1)

= -3





12. The value of sin {(90° - θ)sin θ}/tan θ - 1 is



(a) -cot θ



(b) -sin² θ



(c) -cos² θ



(d) -cosec² θ



Answer


(b) -sin² θ

{(sin(90° - θ)sin θ}/tan θ - 1

= (cosθ sinθ)/(sinθ)/cos θ - 1

= (sin θ cos θ × cos θ)/(sin θ) - 1

= cos² θ - 1

= -(1 - cos² θ)
= - sin² θ

•