Exercise 16.1





1. Use a ruler and compass only in this question.


(i) Draw a circle, centre O and radius 4 cm.


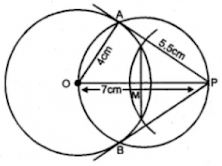
(ii) Mark a point P such that OP = 7 cm.


Construct the two tangents to the circle from P. Measure and record the length of one of the tangents.



Answer

Steps to construct:

Step 1: Draw a circle with center O and radius 4cm and mark that point as A.

Step 2: Take a point P such that OP = 7 cm.

Step 3: Bisect OB at M.

Step 4: With center M and diameter OP, draw another circle intersecting the given circle at A and B.

Step 5: Join PA and PB. Hence PA and PB are pair of tangents to the circle.

Step 6: On measuring PA, it is equal to 5.5 cm.



2.
Draw a line AB = 6 cm. Construct a circle with AB as diameter. Mark a point P at a distance of 5 cm from the mid-point of AB. Construct two tangents from P to the circle with AB as diameter. Measure the length of each tangent



Answer

Steps to construct:

Step 1: Draw a line segment AB = 6 cm.

Step 2: Draw its perpendicular bisector bisecting it at point O.

Step 3: With center O and radius OB, draw a circle.

Step 4: Extend AB to point P such that OP = 5 cm.

Step 5: Draw its perpendicular bisector intersecting it at point M.

Step 6: With center M and radius OM, draw a circle which intersects the given circle at T and S.

Step 7: Join OT, OS, PT and PS. Hence, PT and PS are the required tangents to the given circle.

Step 8: On measuring each tangent is 4cm long. PT = PS = 4 cm.



3.
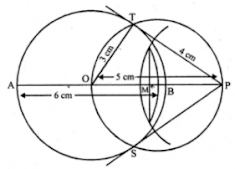
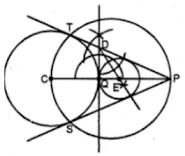
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.



Answer

Steps to construct:

Step 1: Mark a point O.

Step 2: With center O and radius 4 cm and 6 cm, draw two concentric circles.

Step 3: Join OA and mark its mid-point as M.

Step 4: With center M and radius MA, draw another circle which intersects the first circle at P and Q.
Step 5: Join AP and AQ. Hence, AP and AQ are the required tangents to the first circle from point A.







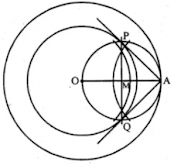
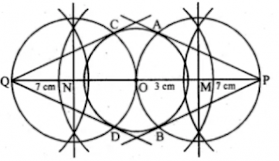
4. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.



Answer
Steps to construct:
Step 1: Consider a point O on a line, with center O, and radius 3cm, draw a circle.
Step 2: Extend its diameters on both sides and cut off OP = OQ = 7cm.
Step 3: Mark the mid-points of OP and OQ as M and N respectively.
Step 4: With Centers M and N and OP and OQ as diameters, draw circles which intersect the given circle at A, B and C, D respectively.
Step 5: Join PA, PB, QC, QD. Hence, PA, PB and QC, QD are the required tangents.



5.
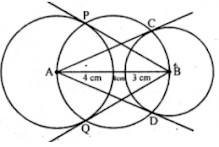
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer
Steps to construct:
Step 1: Draw a line segment AB = 8cm.
Step 2: With center as A and radius 4cm, with center as B and radius 3cm, draw circles.
Step 3: Draw the third circle AB as diameter which intersects the given two circles at C and D, P and Q respectively.
Step 4: Join AC, AD, BP, BQ. Hence, AC and AD, BP and BQ are the required tangents.




Exercise 16.2





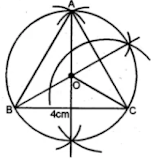
1. Draw an equilateral triangle of side 4 cm. Draw its circumcircle.






Answer
Steps to construct:
Step 1: Draw a line segment BC = 4cm.
Step 2: With centers B and C, draw two arcs of radius 4cm which intersects each other at point A.
Step 3: Join AB and AC.
Step 4: Draw the right bisector of BC and AC intersecting each other at point O.
Step 5: Join OA, OB and OC.
Step 6: With center as O, and radius equal to OB or OC or OA, draw a circle which passes through points A, B and C.
Hence, the required circumcircle of triangle ABC is given below.





2.
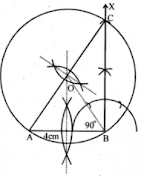
Using a ruler and a pair of compasses only, construct:


(i) A triangle ABC given AB = 4 cm, BC = 6 cm and
∠
ABC = 90
°
.


(ii) A circle which passes through the points A, B and C and mark its centre as O.



Answer

Steps to construct:

Step 1: Draw a line segment AB = 4 cm.

Step 2: At point B, draw a ray BX making an angle of 90^o and cut off BC = 6 cm.

Step 3: Join AC.

Step 4: Draw the perpendicular bisectors of sides AB and AC intersecting each other at point O.

Step 5: With center as O, and radius equal to OB or OA or OC, draw a circle which passes through points A, B, C.





3.
Construct a triangle with sides 3 cm, 4 cm and 5 cm. Draw its circumcircle and measure its radius.



Answer

Steps to construct:

Step 1: Draw a line segment BC = 4 cm.

Step 2: With Center as B and radius 3cm, with center as C and radius 5cm draw two arcs which intersect each other at point A.

Step 3: Join AB and AC.

Step 4: Draw the perpendicular bisector of sides BC and AC which intersects each other at point O.

Step 5: Join OB.

Step 6: With center as O and radius OB, draw a circle which pass through A, B, C.
Step 7: On measuring the radius OB = 2.5 cm.







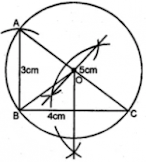
4. Using a ruler and compasses only:

(i) Construe a triangle ABC with the following data:
Base AB = 6 cm, AC = 5.2 cm and
∠
CAB = 60
°
.

(ii) In the same diagram, draw a circle which passes through the points A, B and C and mark its centre O.





Answer
Steps to construct:
Step 1: Draw a line segment AB = 6 cm.
Step 2: At point A, draw a ray making an angle of 60^o.
Step 3: With B as the center and radius 5.2 cm, draw an arc which intersects the ray at C.
Step 4: Join BC.
Step 5: Draw the perpendicular bisector of sides AB and BC which intersects each other at point O.
Step 6: With center as O and radius OA, draw a circle which touches through the points A, B, C.







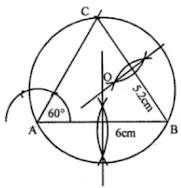
5. Using ruler and compasses only, draw an equilateral triangle of side 5 cm and draw its inscribed circle. Measure the radius of the circle.



Answer
Steps to construct:
Step 1: Draw a line segment BC = 5 cm.
Step 2: With Center as B and radius 5 cm, with center as C and radius 5cm draw two arcs which intersect each other at point A.
Step 3: Join AB and AC.
Step 4: Draw the angle bisector of angles B and C which intersects each other at point I.
Step 5: From I, draw a perpendicular ID on BC.


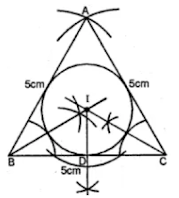
Step 6: With center as I and radius ID, draw a circle which touches the sides of the triangle internally.
Step 7: On measuring the radius ID = 1.5 cm (approx).




6.
(i) Conduct a triangle ABC with BC = 6.4 cm, CA = 5.8 cm and
∠
ABC = 60
°
. Draw its incircle. Measure and record the radius of the incircle.


(ii) Construct a ∆ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.



Answer
Steps to construct:
Step 1: Draw a line segment BC = 6.4 cm.
Step 2: Construct an angle of 60^o at point B.
Step 3: With C as center and radius CA = 5.8 cm, draw an arc cutting BD at A.
Step 4: Join AC.
Step 5: Draw the angle bisector of angle B and angle C which intersect each other at point O.
Step 6: Draw OE perpendicular to BC, intersecting BC at point E.
Step 7: With O as the center and OE as the radius draw the required incircle.
Step 8: On measuring the radius OE = 1.5 cm.


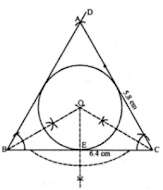
Steps to construct:
Step 1: Draw a line segment BC = 6.5 cm.
Step 2: With B as center and C as center draw arcs AB = 5.5 cm and AC = 5 cm.
Step 3: Join AB and AC.
Step 4: Draw the angle bisectors of B and C. The bisectors meet at point O.
Step 5: With O as the center. Draw an incircle which touches all the sides of the triangle ABC.
Step 6: From point O draw a perpendicular to side BC which cuts at point N.
Step 7: On measuring the radius ON = 1.5 cm.
7. The bisectors of angles A and B of a scalene triangle ABC meet at O.

(i) What is the point O called?
(ii) OR and OQ is drawn a perpendicular to AB and CA respectively. What is the relation between OR and OQ?
(iii) What is the relation between
∠
ACO and
∠
BCO?
dlt26570103614477963965">
Answer
(i) The point O where the angle bisectors meet is called the incenter of the triangle.
(ii) The perpendicular drawn from point O to AB and CA are equal. i.e., OR and OQ.
(iii) ∠ACO = ∠BCO. OC will bisect the ∠C.








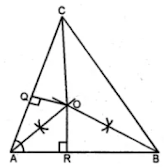
8.
Using ruler and compasses only, construct a triangle ABC in which BC = 4 cm,
∠
ACB = 45
°
and the perpendicular from A on BC is 2.5 cm. Draw the circumcircle of triangle ABC and measure its radius.
Answer
Steps to construct:
Step 1: Draw a line segment BC = 4cm.
Step 2: At point B, draw a perpendicular and cut off BE = 2.5 cm.


Step 3: From, E, draw a line EF parallel to BC.
Step 4: From point C, draw a ray making an angle 45^o which intersects EF at point A.
Step 5: Join AB.
Step 6: Draw the perpendicular bisectors of sides BC and AC intersecting each other at point O.
Step 7: Join OB, OC and OA.
Step 8: With O as the center and radius OB or OC or OA draw a circle which passes through points A, B, C.
Step 9: On measuring the radius OB = 2 cm.





9. Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.



Answer

Steps to construct:

Step 1: Draw a line segment AB = 4 cm.

Step 2: At points A and B draw rays making on angle of 120^o each and cut off AF = BC = 4 cm.

Step 3: At point C and F draw rays making on angle of 120^o each and cut off FE = CD = 4 cm.

Step 4: Join ED. The required ABCDEF hexagon is formed.

Step 5: Draw perpendicular bisectors of sides AB and BC intersecting each other at point O.

Step 6: With O as the center and radius equal OA or OB draw a circle which passes through the vertices of the hexagon.




10.
Draw a regular hexagon of side 4 cm and construct its incircle.



Answer

Steps to construct:


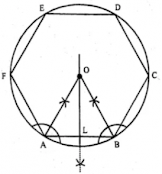
Step 1: Draw a regular hexagon of sides 4 cm.

Step 2: Draw the angle bisector of A and B. which intersects each other at point O.

Step 3: Draw OL perpendicular to AB.
Step 4: With O as the center and radius OB, draw a circle which touches the sides of the hexagon.





Chapter Test





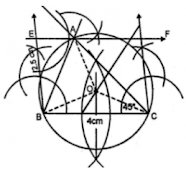
1. Draw a circle of radius 3 cm. Mark its centre as C and mark a point P such that CP = 7 cm. Using ruler and compasses only, Construct two tangents from P to the circle.



Answer

Steps of Construction:

Step 1: Draw a circle with centre C and radius 3 cm.

Step 2: Mark a point P such that CP = 7 cm.

Step 3: With CP as diameter, draw a circle intersecting the given circle at T and S.

Step 4: Joint PT and PS.

Step 5: Draw a tangent at Q to the circle given. Which intersects PT at D.

Step 6: Draw the angle bisector of ∠PDQ intersecting CP at E.

Step 7: With centre E and radius EQ, draw a circle. It will touch the tangent T and PS and the given circle at Q.

2. Draw a line AQ = 7 cm. Mark a point P on AQ such that AP = 4 cm. Using ruler and compasses only, construct:


(i) a circle with AP as diameter.


(ii) two tangents to the above circle from the point Q.



Answer

Steps of construction:

Step 1: Draw a line segment AQ = 7 cm.

Step 2: From AQ, cut off AP = 4 cm

Step 3: With AP as diameter draw a circle with centre O.

Step 4: Draw bisector of OQ which intersect OQ at M.

Step 5: With centre M and draw a circle with radius MQ which intersects the first circle at T and S.

Step 6: Join QT and QS.

QT and QS are the tangents to the first circle.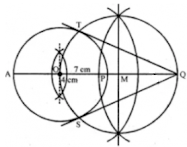






3. Using ruler and compasses only, construct a triangle ABC having given c = 6 cm, b = 1 cm and
∠
A = 30°. Measure side a. Draw carefully the circumcircle of the triangle.



Answer

Steps of Construction:

Step 1: Draw a line segment AC = 7 cm

Step 2: At C, draw a ray CX making an angle of 30°

Step 3: With centre A and radius6 cm draw an arc which intersects the ray CX at B.

Step 4: Join BA.

Step 5: Draw perpendicular bisectors of AB and AC intersecting each other at O.

Step 6: With centre O and radius OA or OB or OC, draw a circle which will pass through A, B and C.
This is the required circumcircle of ΔABC.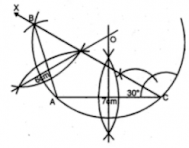



4. Using ruler and compasses only, construct an equilateral triangle of height 4 cm and draw its circumcircle.
Answer
Steps of Construction:
Step 1: Draw a line XY and take a point D on it.
Step 2: At D draw perpendicular and cut off DA = 4 cm.
Step 3: From A, draw rays making an angle of 30° on each side of AD meeting the line XY at B and C.
Now draw a circle perpendicular bisector of AC intersecting AD at O.
Step 4: Now draw perpendicular bisector of AC intersecting AD at O.
Step 5: With centre O and radius OA or OB or OC draw a circle which will pass through A, B and C. This is the required circumcircle of ΔABC.




5. Using ruler and compasses only:
(i) Construct a triangle ABC with the following data: BC = 7 cm, AB = 5 cm and
∠
ABC = 45°.
(ii) Draw the inscribed circle to ΔABC drawn in part (i).
Answer
Steps of construction:
Step 1: Draw a line segment BC = 7 cm.
Step 2: At B, draw a ray BX making an angle of 45° and cut off BA = 5 cm.
Step 3: Join AC.
Step 4: Draw the angle bisectors of ∠B and ∠C intersecting each other at I.
Step 5: From I, draw a perpendicular ID on BC.
Step 6: With centre, I and radius ID, draw a circle which touches the sides of ΔABC at D, E and F respectively. This is the required inscribed circle.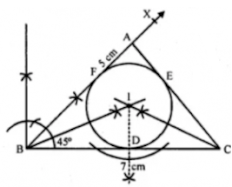



6. Draw a triangle ABC, give that BC = 4 cm, ∠
C = 75° and that radius of the circumcircle of ΔABC is 3 cm.



Answer
Steps of construction:
Step 1: Draw a line segment BC = 4 cm
Step 2: Draw the perpendicular bisector of BC.
Step 3: From B draw an arc of 3 cm radius which intersects the perpendicular bisector at O.
Step 4: Draw a ray CX making art angle of 75°.
Step 5: With centre O and radius 3 cm draw a circle which intersects the ray CX at A.
Step 6: Join AB. ΔABC is the required triangle.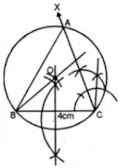



7. Draw a regular hexagon of side 3.5 cm construct its circumcircle and measure its radius.
Answer
Steps of construction:
Step 1: Draw a regular hexagon ABCDF whose each side is 3.5 cm.
Step 2: Draw the perpendicular bisector of AB and BC which intersect each other at O.
Step 3: Join OA and OB.
Step 4: With centre O and radius OA or OB, draw a circle which passes through A, B, C, D, E and P. Then this is the required circumcircle.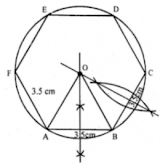




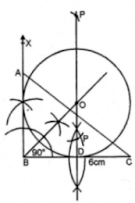
8. Construct a triangle ABC with the following data: AB = 5 cm, BC = 6 cm and
∠
ABC = 90°.
(i) Find a point P which is equidistant from B and C and is 5 cm from A. How many such points are there?
(ii) Construct a circle touching the sides AB and BC, and whose centre is equidistant from B and C.
Answer :
Steps of construction:
Step 1: Draw a line segment BC = 6 cm.
Step 2: At B, draw a ray BX making an angle of 90° and cut off BA = 5 cm.
Step 3: Join AC.
Step 4: Draw the perpendicular bisector of BC.
Step 5: From A with 5 cm radius draw arc which intersects the perpendicular bisector of BC at P and P’.
There are two points.
Step 6: Draw the angle bisectors of ∠B and ∠C intersecting at O
Step 7: From O, draw OD ⊥ BC.
Step 8: With centre O and radius OD, draw a circle which will touch the sides AB and BC. This is the required circle.

•