Exercise 12.1

1. Find the slope of a line
whose inclination is

(i) 45°

(ii) 30°

Answer

(i) tan 45° = 1

(ii) tan 30° =
1/√3

2. Find the inclination of a
line whose gradient is

(i) 1

(ii) √3

(iii) 1/√3

Answer

(i) tan θ = 1 ⇒ θ = 45°

(ii) tan
θ = √3 ⇒ θ = 60°

(iii) tan
θ = 1/√3 ⇒ θ = 30°

3. Find the equation of a
straight line parallel 1 to x-axis is at a distance

(i) 2 units above it

(ii) 3 units below it.

Answer

(i) A
line which is parallel to x-axis is y = a

⇒ y = 2

⇒ y - 2 = 0

(ii) A line which is parallel to x-axis is y = a

⇒ y = -
3

⇒ y + 3
= 0

4. Find the equation of a straight line parallel to
y-axis which is at a distance of :

(i) 3 units to the right.

(ii) 2 units to the left.

Answer

(i) The equation of line parallel
to y-axis is at a distance of 3 units to the right is x = 3

⇒ x - 3
= 0

(ii) The equation of line parallel
to y-axis at a distance of 2 units to the left is x = - 2

⇒ x + 2
= 0

5. Find the equation of a straight line parallel to y-axis and passing through
the point (- 3, 5).

Answer

The equation of the line parallel to y-axis passing through (-3,
5) to x = - 3

⇒ x + 3
= 0

6. Find the equation of a line whose

(i) slope = 3, y-intercept
= - 5

(ii) slope = - (2/7), y-intercept
= 3

(iii) gradient = √3, y-intercept
= - (4/3)

(iv) inclination =
30°, y-intercept = 2

Answer

Equation of a line whose slope and
y-intercept is given is

y = mx + c

where m is the slope and c is the
y-intercept

(i) y = mx + c

⇒ y = 3x
+ (-5)

⇒ y = 3x
- 5

(ii) y = mx + c

⇒ y =
-2/7.x + 3

⇒ 7y = -
21x + 21

⇒ 2x +
7y - 21 = 0

(iii)

(iv) Inclination = 30°

∴ Slope = tan 30° = 1/√3

∴ Equation
y = mx + c

⇒ y =
1/√3 x + 2

⇒ √3y =
x + 2√3

⇒ x -
√3y + 2√3 = 0

7. Find the slope the y-intercept of the following
lines :

(i) x - 2y - 1 = 0

(ii) 4x - 5y - 9 = - 0

(iii) 3x + 5y + 7 = 0

(iv) x/3 + y/4 = 1

(v) y - 3 = 0

(vi) x - 3 = 0

Answer

We know that in the equation

y = mx + c, m is the slope and c is
the y-intercept.

Now using this, we find,

(i) x - 2y - 1 = 0

⇒ x - 1
= 2y

⇒ 2y = x
- 1

⇒ y =
1/2 x - 1/2

Here, slope = 1/2 and y-intercept =
-1/2

(ii) 4x - 5y - 9 = 0

⇒ 4x - 9
= 5y

⇒ 5y =
4x - 9

⇒ y =
4/5 x - 9/5

Here, slope = 4/5 and intercept =
-9/5

(iii) 3x + 5y + 7 = 0

⇒ 5y = - 3x - 7

⇒ y =
-3/5 x - 7/5

Here, slope = -3/5 and y-intercept =
-7/5

(iv) x/3 + y/4 = 1

⇒ 4x +
3y = 12

⇒ 3y = -
4x + 12

⇒ y =
-4/3.x + 12/3

⇒ y =
-4/3 x + 4

Here, slope = -4/3 and y-intercept =
4

(v) y - 3 = 0

⇒ y = 3

⇒ y = 0, x + 3

Here, slope = 0 and y-intercept = 3

(vi) x - 3 = 0

Here in this equation, slope cannot
be defined and does not meet y-axis.

8. The equation of the line PQ is 3y - 3x + 7 = 0

(i) Write down the slope of the line PQ.

(ii) Calculate the angle that the PQ makes with the positive
direction of x-axis.

Answer

Equation of line PQ is 3y - 3x + 7
= 0

Writing in form of y = mx + c

3y = 3x - 7

⇒ y =
3x/3 - 7/3

⇒ y = x
- 7/3

(i) Here slope = l

(ii) ∴ Angle which makes PQ with x-axis
is Q.

But tan θ = 1

∴ θ = 45°

9. The given figure
represents the line y = x + 1 and y = √3x - 1. Write down the angles which the
lines make with the positive direction of the x-axis. Hence determine θ.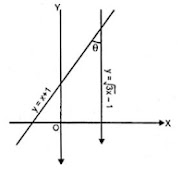



Answer

Slope of
the line y = x + 1 after comparing it with y = mx + c, m = 1

⇒ tan θ = 1

⇒ θ = 45°

and slope
of line y = √3x - 1

m = √3

⇒ tan θ = √3

⇒ θ = 60°

Now in ∆
formed by the given two lines and x-axis.

Ext.
angle = Sum of interior opposite angle.

⇒ 60° = θ + 45°

⇒ θ = 60°
- 45°

= 15°

10. Find the value of p, given that the line y/2 = x
- p passes through the point (- 4, 4).

Answer

Equation of line is y/2 = x - p

It passes through the points (- 4,
4) and it will satisfy the equation

⇒ 4/2 =
- 4 - p

⇒ 2 = -
4 - p

⇒ p = -
4 - 2

⇒ p = -
6

Hence, p = - 6

11. Find the value of p, given that the line y/2 = x
- p passes through the point (-4, 4).

Answer

Equation of line is y/2 = x - p

It passes through the points (- 4,
4) and it will satisfy the equation

⇒ 4/2 =
-4 - p

⇒ 2 = -4 - p

⇒ p = -4 - 2

⇒ p = -6

Hence, p = - 6

11. Given that (a, 2a) lies on the line y/2 = 3x - 6. Find the value of a.



Answer

∵ Point (a, 2a) lies on the line

y/2 = 3x - 6

∴ this point will satisfy the equation

∴ 2a/2 = 3
(a) - 6

⇒ a = 3a - 6

- 3a + a = - 6

⇒ - 2a = - 6

⇒ a = -6/-2

∴ a = 3





12. The graph of the equation y = mx + c passes through the points (1, 4) and (-2, -5). Determine the values of m and c.



Answer

Equation of the line is y = mx + c

∴ It passes through the points (1, 4)

∴ 4 = m×1 + c

⇒ 4 = m + c

Hence, m + c = 4 ...(i)

Again it passes through the point (- 2, - 5)

∴ 5 = m(-2) + c

⇒ 5 = -2m + c

So, 2m - c = 5 ...(ii)

Adding (i) and (iii)

3m = 9

⇒ m = 3

Substituting the value of m in (i)

3 + c = 4

⇒ c = 4 - 3 = 1

Hence, m = 3, c = 1





13. Find the equation of the line passing through the point (2, -5) and making an intercept of -3 on the y-axis.



Answer

∴ The line intersects y-axis making an intercept of -3

∴ The co-ordinates of point of intersect will be (0, - 3)

Now the slope of line (m) = (y₂ - y₁)/(x₂ - x₁)

= (-3+5)/(0 - 2)

= 2/-2

= - 1

∴ Equation of the line will be,

y - y₁ = m(x - x₁)

⇒ y - (-5) = -1(x - 2)

⇒ y + 5 = -x + 2

⇒ x + y + 5 - 2 = 0

⇒ x + y + 3 = 0





14. Find the equation of a straight line passing through (- 1, 2) and whose slope is 2/5.



Answer

Equation of the line will be

y - y₁ = m(x - x₁)

y - 2 = 2/5(x + 1)

⇒ 5y - 10 = 2x + 2

So, 2x - 5y + 2 + 10 = 0

Hence 2x - 5y + 12 = 0





15. Find the equation of a straight line whose inclination is 60° and which passes through the point (0, -3).



Answer

The equation of line whose slope is wand passes through a given point is y - y₁ = m(x - x₁)

Here m = tan 60° = √3 and point is (0, - 3)

∴ y + 3 = √3 (x - 0)

⇒ y + 3 = √3x

⇒ √3x - y - 3 = 0





16. Find the gradient of a line passing through the following pairs of points.


(i) (0, -2), (3, 4)


(ii) (3, -7), (-1, 8)



Answer

m = (y₂ - y₁)/(x₂ - x₁)

Given

(i) (0, - 2), (3, 4)

(ii) (3, - 7), (- 1, 8)

(i) m = (4 + 2)/(3 - 0) = 6/3 = 2

∴ gradient = 2

(ii) m = (8 + 7)/(-1 - 3) = 15/-4

∴ gradient = -(15/4)





17. The coordinates of two points E and F are (0, 4) and (3, 7) respectively. Find:


(i) The gradient of EF


(ii) The equation of EF


(iii) The coordinates of the point where the line EF intersects the x-axis.



Answer

Co-ordinates of points E (0, 4) and F (3, 7) are given, then

(i) The gradient of EF

∴ gradient (m) = (y₂ - y₁)/(x₂ - x₁)

= (7 - 4)/(3 - 0)

= 3/3

= 1

(ii) Equation of line EF,

y - y₁ = m(x - x₁)

⇒ y - 7 = 1(x - 3)

⇒ y - 7 = x - 3

⇒ x - y - 3 + 7 = 0

⇒ x - y + 4 = 0

(iii) Co-ordinates of point of intersection of EF and the x-axis will be y = 0,

Substitutes the value y in the above equation x - y + 4 = 0

⇒ x - 0 + 4 = 0 (∵ y = 0)

⇒ x = - 4

Hence co-ordinates are (- 4, 0)





18. Find the intercepts made by the line 2x - 3y + 12 = 0 on the co-ordinate axis.



Answer

Putting y = 0, we will get the intercept made on x-axis,

2x - 3y + 12 = 0

⇒ 2x - 3×0 + 12 = 0

⇒ 2x - 0 + 2 = 0

⇒ 2x = - 12

And x = - 6

And putting x = 0, we get the intercepts made on y-axis,

2x - 3y + 12 = 0

⇒ 2 × 0 - 3y + 12 = 0

⇒ -3y = - 12

⇒ y = -12/-3

= 4





19. Find the equation of the line passing through the points P (5, 1) and Q (1, -1). Hence, show that the points P, Q and R (11, 4) are collinear.



Answer

The two given points are P (5, 1), Q (1, -1).

∴ Slope of the line (m) = (y₂ - y₁)/(x₂ - x₁) = (- 1 - 1)/(1 - 5)

= -2/-4

= 1/2

Equation of the line,

y - y₁ = m(x - x₁)

⇒ y + 1 = 1/2(x-1)

⇒ 2y + 2 = x - 1

⇒ x - 2y - 1 - 2 = 0

⇒ x - 2y - 3 = 0

If point R (11, 4) be on it, then it will satisfy it.

Now substituting the value of x and y in

11 - 2×4 - 3

= 11 - 8 - 3

= 11 - 11

= 0

∴ R satisfies it.

Hence P, Q and R are collinear.





20. Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.



Answer

Given that

A (a, 3), B (2, 1) and C (5, a) are collinear.

Slope of AB = Slope of BC

⇒ (1 - 3)/(2 - a) = (a - 1)/(5 - 2)

⇒ -2/(2 - a) = (a - 1)/3

⇒ -6 = (a - 1)(2 - a) (Cross-multiplication)

⇒ -6 = 2a - a² - 2 + a

⇒ -6 = 3a - a² - 2

⇒ a² - 3a + 2 - 6 = 0

⇒ a² - 3a - 4 = 0

⇒ a² - 4a + a - 4 = 0

⇒ a(a - 4) + 1(a - 4) = 0

⇒ (a + 1)(a - 4) = 0

⇒ a = -1, or a = 4

a = - 1 (∵ does not satisfy the equation)

∴ a = 4

Slope of BC = (a-1)/(5-2)

= (4-1)/3

= 3/3

= 1 m

Equation of BC ; (y-1) = 1(x-2)

y - 1 = x - 2

⇒ x - y = -1 + 2
⇒ x - y = 1





21. Use a graph paper for this question. The graph of a linear equation in x and y, passes through A (- 1, - 1) and B (2, 5). From your graph, find the values of h and k, if the line passes through (h, 4) and (1/2, k).



Answer

Points (h, 4) and (1/2, k) lie on the line passing through A (- 1, - 1) and B (2, 5)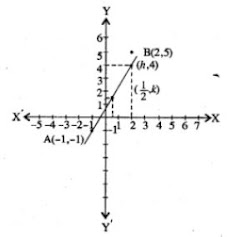


From your graph, we see that h = (3/2) and k = 2.





22. ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, -4). Find


(i) the coordinates of A


(ii) the equation of the diagonal BD.



Answer

Given that

ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, - 4).

(i)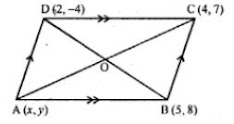




Co-ordinates of O = {(5+2)/2, (8-1 4)/2} = (3.5, 2)

For the line AC

3.5 = (x + 4)/2

2 = (y + 7)/2

⇒ x + 4 = 7

⇒ y + 7 = 4

⇒ x = 7 - 4 = 3

⇒ y = 4 - 7 = - 3

x = 3, y = - 3

Thus, the coordinates of A are (3, - 3)

(ii) Equation of diagonal BD is given by

y - 8 = {(- 4 - 8)/(2 - 5)}.(x - 5)

⇒ y - 8 = {(-12)/(-3)}.(x - 5)

⇒ y - 8 = 4x - 20

⇒ 4x - y - 12 = 0





23. In ∆ABC, A (3, 5), B (7, 8) and C (1, - 10). Find the equation of the median through A.



Answer

AD is median

⇒ D is mid point of BC

∴ D is (7+1)/2, (8-10)/2}

i.e., (4, -1)

Slope of AD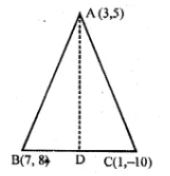


m = (y₂ - y₁)/(x₂ - x₁)

= (5+1)/(3-4) = 6/-1 = - 6

∴ Equation of AD

y - y₁ = m(x - x₁)

⇒ y + 1 = - 6(x - 4)

⇒ y + 1 = - 6x + 24

⇒ y + 6x = - 1 + 24

⇒ 6x + y = 23





24. Find the equation of a line passing through the point (-2, 3) and having x-intercept 4 units.



Answer

x-intercept = 4

∴ Co-ordinates of the point will be (4, 0)

Now slope of the line passing through the points (- 2, 3) and (4, 0)

(m) = (y₂ - y₁)/(x₂ - x₁)

= (0 - 3)/(4 + 2)

= - 3/6

= - (1/2)

∴ Equation of the line will be y - y₁ = m(x - x₁)

⇒ y - 0 = - {1/2(x - 4)}

⇒ 2y = - x + 4

⇒ x + 2y = 4

or, x + 2y - 4 = 0





25. Find the equation of the line whose x-intercept is 6 and y-intercept is - 4.



Answer

x-intercept = 6

∴ The line will pass through the point (6, 0)

y - intercept = - 4

⇒ c = - 4

∴ The line will pass through the point (0, - 4)

Now m = (y₂ - y₁)/(x₂ - x₁)

= (-4-0)/(0-6)

= -4/-6

= 2/3

∴ Equation of line will be y = mx + c

⇒ y = 2/3 x + (-4) = 2/3 x - 4

⇒ 3y = 2x - 12
⇒ 2x - 3y = 12





26. Write down the equation of the line whose gradient is 1/2 and which passes through P where P divides the line segment joining A (- 2, 6) and B (3, - 4) in the ratio 2 : 3.



Answer

P divides the line segment joining the points A (- 2, 6) and (3, - 4) in the ratio 2 : 3.

∴ Co-ordinates of P will be

x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {2×3 + 3×(-2)}/(2+3)

= (6 - 6)/5

= 0/5

= 0

y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {2×(-4) + 3×6}/(2 + 3)

= (- 8 + 18)/5

= 10/5

= 2

∴ Co-ordinates are (0, 2)

Now slope (m) of the line passing through (0, 2) = 3/2

∴ Equation of the line will be

y - y₁ = m(x - x₁)

⇒ y - 2 = 3/2 (x - 0)

⇒ 2y - 4 = 3x

⇒ 3x - 2y + 4 = 0





27. Find the equation of the line passing through the point (1, 4) and intersecting the line x - 2y - 11 = 0 on the y-axis.



Answer

Line x - 2y - 11 = 0 passes through y-axis

x = 0,

Now substituting the value of x in the equation x - 2y - 11 = 0

∴ - 2y - 11 = 0

⇒ - 2y = 11

⇒ y = - (11/2)

∴ Co-ordinates of point will be (0, - 11/2)

Now slope of the line joining the points (1, 4) and (0, - 11/2)

m = (y₂ - y₁)/(x₂ - x₁) = (- 11/2 - 4)/(0-1)

= (-19/2)/(-1)

= 19/2

And equation of the line will be

y - y₁ = m(x - x₁)

⇒ y + 11/2 = 19/2×(x - 0)

⇒ 2y + 11 = 19x

⇒ 19x - 2y - 11 = 0





28. Find the equation of the straight line containing the point (3, 2) and making positive equal intercepts on axes.



Answer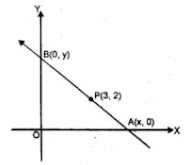


Let the line containing the point P (3, 2) passes through x-axis at A (x, 0) and y-axis at B (0, y)

OA = OB given

∴ x = y

Now slope of the line (m) = (y₂ - y₁) = (x₂ - x₁)

= (0 - y)/(x - 0) = - x/x = - 1 (∵ x = y)

∴ Equation of the line will be

y - y₁ = m(x - x₁)

⇒ y - 2 = -1×(x - 3)

⇒ y - 2 = -x + 3

⇒ x + y - 2 - 3 = 0

⇒ x + y - 5 = 0

⇒ x + y = 5





29. Three vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find :


(i) the coordinates of the fourth vertex D.


(ii) length of diagonal BD.


(iii) equation of side AB of the parallelogram ABCD.



Answer

Three vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2)

(i) We need to find the co-ordinates of D

We know that the diagonals of a parallelogram bisect each other

Let (x, y) be the co-ordinates of D

∴ Mid-point of diagonal AC = {(3 + 3)/2, (6 + 2)/2}

= (3, 4)

And, mid-point of diagonal BD = {(5 + x)/2, (10 + y)/2}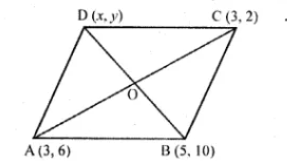


Thus, we have

(5 + x)/2 = 3 and (10 + y)/2 = 4

⇒ 5 + x = 6 and 10 + y = 8

⇒ x = 1 and y = - 2

∴ Co-ordinate of D = (1, - 2)

(ii)


(iii) Equation of the side joining A (3, 6) and D (1, - 2) is given by

(x - 3)/(3 - 1) = (y - 6)/(6 + 2)

⇒ (x - 3)/2 = (y - 6)/8

⇒ 4(x - 3) = y - 6

⇒ 4x - 12 = y - 6

⇒ 4x - y = 6

Thus, the equation of the side joining A (3, 6) and D (1, - 2) is 4x - y = 6





30. A and B are two points on the x-axis and y-axis respectively. P (2, - 3) is the mid point of AB. Find the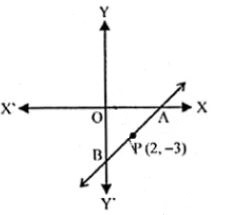






(i) the co-ordinates of A and B.


(ii) the slope of the line AB.


(iii) the equation of the line AB.



Answer

Points A and B on x-axis and y-axis respectively

Let co-ordinates of A be (X, O) and of B be (O, Y)

P (2, - 3) is the midpoint of AB

Then, 2 = (X + O)/2 and - 3 = (O + Y)/2

⇒ x = 4, y = - 6

(i) Hence, co-ordinates of A are (4, 0) and of B are (0, - 6)

(ii) Slope of AB = (y₂ - y₁)/(x₂ - y₁)

= (-6 - 0)/(0-4)

= -6/-4

= 3/2

(iii) Equation of AB will be y - y₁ = m(x - x₁)

⇒ y = (-3) = 3/2 (x - 2) (∵ P lies on it)

⇒ y + 3 = 3/2 (x - 2)

⇒ 2y + 6 = 3x - 6

⇒ 3x - 2y = 6 + 6
⇒ 3x - 2y = 12





31. Find the equations of the diagonals of a rectangle whose sides are x = - 1, x = 2, y = - 2 and y = 6.



Answer

The equations of sides of a rectangle whose equations are

x₁ = - 1, x₂ = 2, y₁ = - 2, y₂ = 6.

These lines form a rectangle when they intersect at A, B, C, D respectively.

Co-ordinates of A, B, C and D will be

(- 1, - 2), (2, - 2), (2, 6) and (- 1, 6) respectively.

AC and BD are its diagonals

(i) Slope of the diagonal AC = (y₂ - y₁)/(x₂ - x₁)

= (6 + 2)/(2 + 1)

= 8/3

∴ Equation of AC will be

y - y₁ = m(x - x₁)

= y + 2 = 8/3 (x + 1)

⇒ 3y + 6 = 8x + 8

8x - 3y + 8 - 6 = 0

⇒ 8x - 3y + 2 = 0





32. Find the equation of a straight line passing through the origin and through the point of intersection of the lines 5x + 1y - 3 and 2x - 3y = 7



Answer

5x + 7y = 3 ...(i)

2x - 3y = 7 ...(ii)

Multiply (i) by 3 and (ii) by 7,

15x + 21y = 9

14x - 21y = 49

Adding we get,

29x = 58

⇒ x = 58/29 = 2

Substituting the value of x in (i)

5 × 2 + 7y = 3

⇒ 10 + 7y = 3

⇒ 7y = 3 - 10

⇒ 7y = - 7

⇒ y = - 1

∴ Point of intersection of lines is (2, -1)

Now slope of the line joining the points (2, -1) and the origin (0, 0)

m = (y₂ - y₁)/(x₂ - x₁)

= (0 + 1)/(0 - 2)

= 1/2

Equation of line will be

y - y₁ = m(x - x₁)

⇒ y - 0 = - 1/2×(x - 0)

⇒ 2y = -x

⇒ x + 2y = 0





33. Point A (3, -2) on reflection in the x-axis is mapped as A’ and point B on reflection in the y-axis is mapped onto B’ (- 4, 3).


(i) Write down the co-ordinates of A’ and B.


(ii) Find the slope of the line A’B, hence find its inclination.



Answer

(i) A’ is the image of A (3, -2) on reflection in the x-axis.

∴ Co-ordinates of A’ will be (3, 2)

Again B’ (- 4, 3) in the image of A’, when reflected in the y-axis

∴ Co-ordinates of B will be (4, 3)

(ii) Slope of the line joining, the points A’ (3, 2) and B (4, 3)

= (y₂ - y₁)/(x₂ - x₁) = (2 - 3)/(3 - 4)

= -1/-1

= 1

Now tan θ= 1

∴ θ = 45°

Hence angle of inclination = 45°





Exercise 12.2
dlt26111241319475994903">


1. State which one of the following is true : The straight line y = 3x - 5 and 2y = 4x + 7 are


(i) Parallel


(ii) Perpendicular


(iii) neither nor perpendicular.



Answer

Slope of line y = 3x - 5 = 3

And slope of line = 4x + 7

⇒ y = 2x + 7/2 = 2

∴ Slope of both lines are neither equal nor their product is -1.

∴ These line are neither parallel nor perpendicular.





2. If 6x + 5y - 7 = 0 and 2px + 5y + 1 = 0 are parallel lines, find the value of p.



Answer

In equation

6x + 5y - 7 = 0

⇒ 5y = -6x + 7

⇒ y = -(6/5)x + 2/5

∴ Slope (m) = -6/5 ...(i)

Again in equation 2px + 5y + 1 = 0

⇒ 5y = - 2px - 1

⇒ y = -2/5 px - 1/5

∴ Slope (m) = -2/5 p ...(ii)

∵ lines are parallel

m₁ = m₂

From (i) and (ii) - (6/5) = -(2p/5)

⇒ p = -6/5 × (-5/2)

= 3





3. Lines 2x - by + 5 = 0 and ax + 3y = 2 are parallel. Find the relation connecting a and b.



Answer

In equation 2x - by + 5 = 0

⇒ -by = -2x - 5

⇒ y = 2/b + 5/b

Slope (m) = 2/b

And in equation ax + 3y = 2

⇒ 3y = -ax + 2

⇒ y = -(a/3)×x + 2/3

∴ slope (m₂) = -(a/3)

∵ Lines are parallel

∴ m₁ = m₂

⇒ 2/b = -(a/3)

⇒ - ab = 6

⇒ ab = -6





4. Given that the line y/2 = x - p and the line ax + 5 = 3y are parallel, find the value of a.



Answer

In equation y = x - p

⇒ y = 2x - 2p

Slope (m₁) = 2

In equation ax + 5 = 3y

⇒ y = a/3 ×x + 5/3

Slope (m₂) = a/3

∵ Lines are parallel

∴ m₁ = m₂

a/3 = 2

⇒ a = 6





5. If the lines y = 3x + 7 and 2y + px = 3 perpendicular to each other, find the value of p.



Answer

Gradient m₁ of the line y = 3x + 7 is 3

2y + px = 3

⇒ y = (-px)/2 + 3/2

Gradient m² of this line is - (p/2)

Since, the given lines are perpendicular to each other.

∴ m₁ × m₂ = - 1

⇒ 3 × (-p/2) = - 1
⇒ p = 2/3
6. If the straight lines 3x - 5y + 4 = 0 and 4x - 2y + 5 = 0 are perpendicular to each other.
Answer
Given
In equation, 3x - 5y + 4 = 0
⇒ 5y = kx + 4
⇒ y = k/5 + 4/5
∴ Slope (m₁) = k/5
And in equation, 4x - 2y + 5 = 0
⇒ 2y = 4x + 5
⇒ y = 2x + 5/2
Slope (m₂) = 2
∵ Lines are perpendicular to each other
∴ m₁m₂ = - 1
k/5 × 2 = - 1
⇒ k = (-1 × 5)/2
= -5/2
7. If the lines 3x + by + 5 = 0 and ax - 5y + 7 = 0 are perpendicular to each other, find the relation connecting a and b.
Answer
Given,
In the equation 3x + by + 5 = 0
by = -3x - 5
⇒ y = -3/b ×x - 5/b
Slope (m₁) = -3/b
And in the equation ax - 5y + 7 = 0
⇒ 5y = ax + 7
⇒ y = a/5 + 7/5
∴ Slope (m₂) = a/5
∵ Lines are perpendicular to each other
∴ m₁m₂ = - 1
⇒ -3/b × a/5 = - 1
⇒ - 3a/5b = - 1
⇒ - 3a = - 5b
⇒ 3a = 5b
8. Is the line through (-2, 3) and (4, 1) perpendicular to the line 3x = y + 1? Does the line 3x = y + 1 bisect the join of (-2, 3) and (4, 1).
Answer
Slope of the line passing through the points (- 2, 3) and (4, 1) = (y₂ - y₁)/(x₂ - x₁)
= (1 - 3)/(4 + 2)
= -2/6
= -1/3
Slope of line 3x = y + 1
∵ m₁ × m₂ = -1/3 × 3 = - 1
∴ These lines are perpendicular to each other
Co-ordinates of mid-point of line joining the points (-2, 3) and (4, 1) will be {(-2+4)/2, (3+1)/2} or (2/2, 4/2) or (1, 2).
If mid-point (1, 2) lies on the line 3x = y + 1 then it will satisfy it.
Now substituting the value of x and y is 3x = y + 1
⇒ 3 ×1 = 2 + 1
⇒ 3 = 3 which is true.
Hence the line 3x = y + 1 bisects the line joining the points (-2, 3), (4, 1).
9. The line through A (- 2, 3) and B (4, b) is perpendicular to the line 2x - 4y = 5. Find the value of b.
Answer
Gradient (m₁) of the line passing through the points A (- 2, 3) and B (4, b)
= (b - 3)/(4 + 2)
= (b - 3)/6
Gradient (m₂) of the line 2x - 4y = 5
Or y = x/2 - 5/2 is 1/2
Since, the lines are perpendicular to each other,
∴ m₁ × m₂ = - 1
(b - 3)/6 × 1/2 = - 1
⇒ (b - 3)/12 = - 1
⇒ b - 3 = - 12
⇒ b = - 9
10. If the lines 3x + y = 4, x - ay + 7 = 0 and bx + 2y + 5 = 0 from three consecutive sides of a rectangle, find the value of a and b.
Answer
In the line 3x + y = 4 ...(i)
⇒ y = -3x + 4
Slope (m₁) = - 3
In the line x - ay + 7 = 0 ...(ii)
⇒ ay = x + 7
⇒ y = (1/a)×x + 7/a
Slope (m₂) = 1/a
And in the line bx + 2y + 5 = 0 ...(iii)
⇒ 2y = -bx - 5
⇒ y = (-b/2) ×x - 5/2
∴ Slope (m₃) = - b/2
∵ These are the consecutive three sides of a rectangle.
∴ (i) and (ii) are perpendicular to each other
∴ m₁m₂ = - 1
⇒ -3 × 1/a = - 1
⇒ -3 = - a
⇒ a = 3
And (i) and (ii) are parallel to each other
∴ m₁ = m₃
⇒ -3 = (- b)/2
⇒ -b = - 6
⇒ b = 6
Hence a = 3, b = 6
11. Find the equation of a line, which has the y-intercept 4, and is parallel to the line 2x - 3y - 7 = 0. Find the coordinates of the point where it cuts the x-axis.
Answer
In the given line 2x - 3y - 7 = 0
⇒ 3y = 2x - 7
⇒ y = (2/3)×x - 7/3
Hence slope (m₁) = 2/3
∴ Equation of the line parallel to the given line will be
y - y₁ = m(x - x₁)
∵ it passes through (0, 4), then
y - 4 = 2/3(x - 0)
⇒ 3y - 12 = 2x
⇒ 2x - 3y + 12 = 0 ...(i)
Now let it intersect x-axis at (x, y)
∴ y = 0
Substitute the value of y in (i)
2x - 3×0 + 12 = 0
⇒ 2x = - 12
x = - 6
12. Find the equation of a straight line perpendicular to the line 2x + 5y + 7 = 0 and with y-intercept - 3 units.
Answer
In the line 2x + 5y + 7 = 0
⇒ 5y = -2x - 7
⇒ y = (-2/5)×x - 7/5
Here slope (m₁) = -(2/5)
Let the slope of the line perpendicular to the given line = m₂
∴ m₁m₂ = - 1
⇒ -(2/5)m₂ = - 1
∴ m₂ = -1 × -5/2
= 5/2
∵ It makes y-intercept -3 units
∴ The point where it passes = (0, -3)
∴ Equations of the new line,
y - y₁ = m(x - x₁)
⇒ y - (-3) = 5/2×(x - 0)
⇒ y + 3 = (5/2)×x
⇒ 2y + 6 = 5x
⇒ 5x - 6y - 6 = 0
13. Find the equation of a straight line perpendicular to the line 3x - 4y + 12 = 0 and having same y-intercept as 2x - y + 5 = 0.
Answer
In the given line 3x - 4y + 12 = 0
⇒ 4y = 3x + 12
⇒ y = (3/4)x + 3
Here slope (m₁) = 3/4
Let the slope of the line perpendicular to the given line be = m₂
∴ m₁m₂ = - 1
⇒ 3/4m₂ = - 1
m₂ = -4/3
y-intercept in the equation
2x - y + 5 = 0
⇒ 2×0 - y + 5 = 0
⇒ y = 5
∴ The equation of the line passing through (0, 5) will be
y - y₁ = m(x - x₁)
⇒ y - 5 = -4/3 ×(x - 0)
⇒ 3y - 15 = - 4x
⇒ 4x + 3y - 15 = 0
14. Find the equation of the line which is parallel to 3x - 2y = - 4 and passes through the point (0, 3).
Answer
In the given line 3x - 2y = - 4
⇒ 2y = 3x + 4
⇒ y = 3/2×x + 2
Here slope (m₁) = 3/2
∴ Slope of the line parallel to the given line = 3/2 and passes through (0, 3)
∴ Equation of the line will be y - y₁ = m(x - x₁)
⇒ y - 3 = 3/2 × (x - 0)
⇒ 2y - 6 = 3x
⇒ 3x - 2y + 6 = 0
15. Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.
Answer
In the given equation 3x + 5y + 15 = 0
⇒ 5y = - 3x - 15
⇒ y = -3/5 ×(x - 3)
How slope (m₁) = -3/5
∴ Slope of the line parallel to the given line = -3/5 and passes through the point (0, 4)
∴ Equation of the line will be
y - y₁ = m(x - x₁)
⇒ y - 4 = -3/5 ×(x - 0)
5y - 20 = -3x
⇒ 3x + 5y - 20 = 0
16. The equation of a line is y = 3x - 5. Write down the slope of this line and the intercept made by it on the y-axis. Hence or otherwise, write down the equation of a line which is parallel to the line and which passes through the point (0, 5).
Answer
In the given line y = 3x - 5
Here slope (m₁) = 3
Substituting x = 0, then y = - 5
y- intercept = - 5
The slope of the line parallel to the given line will be 3 and passes through the point (0, 5).
Equation of the line will be
y - y₁ = m(x - x₁)
⇒ y - 5 = 3(x - 0)
⇒ y - 5 = 3x
⇒ 3x - y + 5 = 0
⇒ y = 3x + 5
17. Write down the equation of the line perpendicular to 3x + 8y = 12 and passing through the point (-1, -2).
Answer
In the given line 3x + 8y = 12
⇒ 8y = - 3x + 12
⇒ y = -3/8 ×x + 12/8
Here slope (m₁) = -3/8
Let the slope of the line perpendicular to the given line be = m₂
∴ m₁m₂ = -1
⇒ -3/8 × m₂ = -1
m₂ = 8/3
∴ Equation of the line where slope is 8/3 and passes through the point (-1, -2) will be
y - y₁ = m(x - x₁)
⇒ y - (-2) = 8/3 [x - (-1)]
⇒ y + 2 = 8/3(x + 1)
⇒ 3y + 6 = 8x + 8
⇒ 8x - 3y + 8 - 6 = 0
⇒ 8x - 3y + 2 = 0
18. (i) The line 4x - 3y + 12 = 0 meets the x-axis at A. Write down the co-ordinates of A.
(ii) Determine the equation of the line passing through A and perpendicular to 4x - 3y + 12 = 0.
Answer
(i) In the line 4x - 3y + 12 = 0 ...(i)
3y = 4x + 12
⇒ y = 4/3 ×x + 4
Here slope (m₁) = 4/3
Let the slope of the line perpendicular to the given line be = m₂
∴ m₁m₂ = - 1
⇒ 4/3 ×m₂ = - 1
⇒ m₂ = -3/4
Let the point on x-axis be A (x, 0)
∴ Substituting the value of y in (i)
4x - 3×0 + 12 = 0
⇒ 4x + 12 = 0
⇒ 4x = -12
⇒ x = -3
∴ Co-ordinates of A will be (- 3, 0)
(ii) Equation of the line perpendicular to the given line passing through A will be.
y - y₁ = m(x - x₁)
⇒ y - 0 = -3/4 ×(x + 3)
⇒ 4y = - 3x - 9
⇒ 3x + 4y + 9 = 0
19. Find the equation of the line that is parallel to 2x + 5y - 7 = 0 and passes through the mid-point of the line segment joining the points (2, 7) and (- 4, 1).
Answer
The given line 2x + 5y - 7 = 0
5y = - 2x + 7
⇒ y = -2/5 ×x + 7/5
Here slope (m₁) = -2/5
∴ Slope of the line parallel to the given line will be -2/5.
Co-ordinates of the mid-point joining the points (2, 7) and (-4, 1) will be = {(2-4)/2, (7+1)/2} or (-2/2, 8/2) or (-1, 4)
∴ Equation of the line will be,
y - y₁ = m(x - x₁)
⇒ y - 4 = -2/5 ×(x + 1)
⇒ 5y - 20 = -2x - 2
⇒ 2x + 5y - 20 + 2 = 0
⇒ 2x + 5y - 18 = 0
20. Find the equation of the line that is perpendicular to 3x + 2y - 8 = 0 and passes through the mid-point of the line segment joining the points (5, -2), (2, 2).
Answer

In the given line 3x + 2y - 8 = 0
⇒ 2y = -3x + 8
⇒ y = -3/2 ×x + 4
Here slope (m₁) = -3/2
Co-ordinates of the mid-point of the line segment joining the points (5, -2) and (2, 2) will be {(5+2)/2, (-2+2)/2} or (7/2, 0)
And let the slope of the line perpendicular to the given line be = m₂
∴ m₁m₂ = - 1
⇒ -3/2 m₂ = - 1
⇒ m₂ = 2/3
∴ Equations of the line perpendicular to the given line and passing through (7/2, 0) will be.
y - y₁ = m(x - x₁)
⇒ y - 0 = 2/3(x - 7/2)
⇒ 3y = 2x - 7
⇒ 2x - 3y - 7 = 0
26. Show that the triangle formed by the points A (1, 3), B (3, - 1) and C (- 5, - 5) is a right angled triangle by using slopes.
Answer
Slope (m₁) of line by joining the points A (1, 3), B (3, - 1) = (y₂ - y₁)/(x₂ - x₁)
∴ m₁ = (-1-3)/(3-1) = -4/2 = - 2
Slope (m₂) of the line joining the points B
(3, -1) and C (-5, -5) = (y₂-y₁)/(x₂-x₁)
⇒ m₂ = (-5+1)/(-5-3)
= (-4/-8)
= 1/2
∴ m₁ × m₂ = -2 × 1/2 = -1
∴ Lines AB and BC are perpendicular to each other.
Hence ∆ABC is a right angled triangle.
27. Find the equation of the line through the point (- 1, 3) and parallel to the line joining the points (0, - 2) and (4, 5).
Answer
Slope of the line joining the points (0, - 2) and (4, 5) = (y₂ - y₁)/(x₂ - x₁)
= (5+2)/(4-0)
= 7/4
Slope of the line parallel to it passing through (-1, 3) = 7/4
And equation of the line
y - y₁ = m(x - x₁)
⇒ y - 3 = 7/4 ×(x + 1)
⇒ 4y - 12 = 7x + 7
⇒ 7x - 4y + 7 + 12 = 0
⇒ 7x - 4y + 19 = 0
28. A (- 1, 3), B (4, 2) , C (3, - 2) are the vertices of a triangle.
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC.
Answer
Given, A (- 1, 3), B (4, 2), C (3, - 2)
(i) Coordinates of centroid G = {(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3}
= {(-1 + 4 + 3)/3, (3 + 2 - 2)/3}
= (6/3, 3/3)
= (2, 1)
So, the coordinates are (2, 1)
(ii) Slope of AC = (y₂ - y₁)/(x₂ - x₁) = (-2 -3)/{(3-(-1)}
= -5/4
∴ Slope of the required line (m) = -5/4
Let the equation of the line through G, be y - y₁ = m(x - x₁)
⇒ y - 1 = -5/4 ×(x-2)
⇒ 4y - 4 = -5x + 10
⇒ 5x + 4y - 14 = 0 which is the required line.
29. The line through P (5, 3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the coordinates of Q.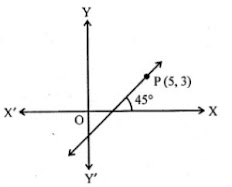






Answer
(i) Here θ = 45°
So, slope of the line = tan θ
= tan 45°
= 1
(ii) Equation of the line through P and Q is y -3 = 1(x - 5)
⇒ y - x + 2 = 0
(iii) Let the coordinates of Q be (0, y)
Then m = (y₂ - y₁)/(x₂ - x₁)
⇒ 1 = (3 - y)/(5 - 0)
⇒ 5 = 3 - y
⇒ y = -2
So, coordinates of Q are (0, -2)
30. In the adjoining diagram, write down
(i) the co-ordinates of the points A, B and C.
(ii) The equation of the line through A parallel to BC.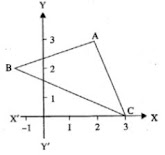






Answer
From the given figure, it is clear that co-ordinates of A are (2, 3) of B are (- 1, 2) and of C are (3, 0).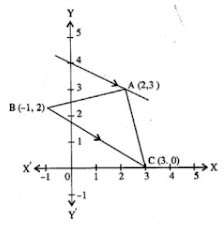


Now slope of BC (m) = (y₂ - y₁)/(x₂ - x₁)
= (0 - 2)/{3 - (-1)}
= -2/(3+1)
= -2/4
= -1/2
∴ Slope of line parallel to BC = -1/2
∵ It passes through A (2, 3)
∴ Its equations will be, y - y₁ = m(x - x₁)
⇒ y - 3 = -1/2 ×(x - 2)
⇒ 2y - 6 = -x + 2
⇒ x + 2y = 2 + 6
⇒ x + 2y = 8
31. Find the equation of the through (0, -3) and perpendicular to the line joining the points (- 3, 2) and (9, 1).
Answer
The slope (m₁) of the line joining the points (- 3, 2) and (9, 1)
= (y₂ - y₁)/(x₂ - x₁)
= (1 - 2)/(9 + 3)
= -1/12
Let slope of the line perpendicular to the line = m₂
∴ m₁m₂ = -1
⇒ -1/12 × m₂ = -1
⇒ m₂ = -1 × (-12/1)
= 12
∴ Equation of the line passing through (0, -3) and of slope m₂ = 12
y - y₁ = m(x - x₁)
⇒ y + 3 = 12(x - 0)
⇒ y + 3 = 12x
⇒ 12x - y - 3 = 0






32. The vertices of a triangle are A (10, 4), B (4, - 9) and C (- 2, - 1). Find the equation of the altitude through A. The perpendicular drawn from a vertex of a triangle to the opposite side is called altitude.
Answer
Vertices of ∆ABC are A (10, 4), B (4, - 9) and C (-2, -1)
Slope of the line BC (m₁) = (y₂ - y₁)/(x₂ - x₁)
= (-1 + 9)/(-2 - 4)
= 8/(-6)
= -4/3
Let the slope of the altitude from A (10, 4) to BC = m₂
∴ m₁m₂ = -1
⇒ -4/3 × m₂ = -1
⇒ m₂ = -1 ×(-3/4) = 3/4
∴ Equation of the line will be,
y - y₁ = m(x - x₁)
⇒ y - 4 = 3/4 ×(x - 10)
⇒ 4y - 16 = 3x - 30
⇒ 3x - 4y + 16 - 30 = 0
⇒ 3x - 4y - 14 = 0
33. A (2, - 4), B (3, 3) and C (-1, 5) are the vertices of triangle ABC. Find the equation of :
(i) the median of the triangle through A
(ii) the altitude of the triangle through B
Answer
(i) D is the mid-point of BC
Co-ordinates of D will {(3 - 1)/2, (3 + 5)/2} or {(2/2, 8/2)} or (1, 4)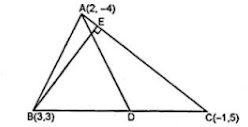


∴ Slope of median AD
(m) = (y₂ - y₁)/(x₂ - x₁)
= (4 + 4)/(1 - 2)
= 8/-1
= -8
Then equation of AD will be,
y - y₁ = m(x - x₁)
⇒ y - 4 = -8 (x - 1)
⇒ y - 4 = -8x + 8
⇒ 8x + y - 4 - 8 = 0
⇒ 8x + y - 12 = 0
(ii) BE is the altitude from B to AC
∴ Slope of AC (m₁) = (y₂ - y₁)/(x₂ - x₁)
= (5 + 4)/(- 1 - 2)
= 9/-3
= -3
Let slope of BE = m₂
But m₁m₂ = -1
⇒ - 3×m₂ = -1
m₂ = -1/-3 = 1/3
∴ Equation of BE will be,
y - y₁ = m(x - x₁)
⇒ y - 3 = 1/3 ×(x - 3)
⇒ 3y - 9 = x - 3
⇒ x - 3y - 3 + 9 = 0
⇒ x - 3y + 6 = 0
34. Find the equation of the right bisector of the line segment joining the points (1, 2) and (5, - 6).
Answer
Slope of the line joining the points (1, 2) and (5, 6)
m₁ = (y₂ - y₁)/(x₂ - x₁)
= (-6 - 2)/(5 - 1)
= -8/4
= -2
Let m₂ be the right bisector of the line
∴ m₁m₂ = -1
⇒ -2 × m₂ = -1
m₂ = (-1/-2) = 1/2
mid-point of the line segment joining (1, 2) and (5, -6) will be {(1 + 5)/2, (2 - 6)/2} or (6/2, -4/2) or (3, -2)
∴ Equation of line, the right bisector will be y - y₁ = m(x - x₁)
⇒ y + 2 = 1/2 ×(x - 3)
⇒ 2y + 4 = x - 3
⇒ x - 2y - 3 - 4 = 0
⇒ x - 2y - 7 = 0
35. Points A and B have coordinates (7, -3) and (1, 9) respectively. Find
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of ‘p’ if (-2, p) lies on it.
Answer
Coordinates of A are (7, -3), of B = (1, 9)
(i) ∴ Slope (m) = (y₂ - y₁)/(x₂ - x₁)
= {9 - (-3)}/(1 - 7)
= (9+3)/(1 - 7)
= 12/-6
= -2
(ii) Let PQ is the perpendicular bisector of AB intersecting it at M.
∴ Co-ordinates of M will be = (x₁ + x₂)/2, (y₁ + y₂)/2
= (7 + 1)/2, (-3 + 9)/2
= 8/2, 6/2 or (4, 3)
∴ Slope of PQ = 1/2 (m₁, m₂ = -1)
∴ Equation of PQ = y - y₁ = m(x - x₁)
⇒ y - 3 = 1/2 ×(x - 4)
⇒ 2y - 6 = x - 4
⇒ x - 2y + 6 - 4 = 0
⇒ x - 2y + 2 = 0
(iii) ∵ Point (-2, p) lies on it
∴ - 2 - 2p + 2 = 0
⇒ -2p + 0 = 0
⇒ -2p = 0
∴ p = 0
36. The points B (1, 3) and D (6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.
Answer
Slope of BD (m₁) = (y₂ - y₁)/(x₂ - x₁)
= (8 - 3)/(6 - 1)
= 5/5
= 1
Diagonal AC is perpendicular bisector of diagonal BD
∴ Slope of AC = -1 (∵ m₁m₂ = -1)
And co-ordinates of midpoint of BD will be {(1 + 6)/2, (3 + 8)/2} or (7/2, 11/2)
∴ Equation of AC,
y - y₁ = m(x - x₁)
⇒ y - 11/2 = -1 ×(x - 7/2)
⇒ y - 11/2 = -x + 7/2
⇒ 2y - 11 = -2x + 7
⇒ 2x + 2y - 11 - 7 = 0
⇒ 2x + 2y - 18 = 0
Or x + y - 9 = 0
37. ABCD is a rhombus. The co-ordinates of A and C are (3, 6) and (- 1, 2) respectively. Write down the equation of BD.
Answer
Co-ordinates of A (3, 6), C (-1, 2)
Slope of AC (m₁) = (y₂ - y₁)/(x₂ - x₁)
= (2 - 6)/(-1 - 3)
= -4/-4
= 1
∴ Slope of BD = - 1 (∵ m₁m₂ = -1)
And co-ordinates of mid point of AC will be {(3 - 1)/2, (6 + 2)/2} or (2/2, 8/2) or (1, 4)
∴ Equation of BD will be,
y - y₁ = m(x - x₁)
⇒ y - 4 = -1(x - 1)
⇒ y - 4 = -x + 1
⇒ x + y - 4 - 1 = 0
⇒ x + y - 5 = 0
38. Find the equation of the line passing through the intersection of the lines 4x + 3y = 1 and 5x + 4y = 2 and
(i) parallel to the line x + 2y - 5 = 0
(ii) perpendicular to the x-axis.
Answer
4x + 3y = 1 ...(i)
5x + 4y = 2 ...(ii)
Multiplying (i) by 4 and (ii) by 3
16x + 12y = 4
15x + 12y = 6
Subtracting (i) from (ii),

x = -2
Substituting the value of x in (i)
4(-2) + 3y = 1
⇒ -8 + 3y = 1
⇒ 3y = 1+8 = 9
⇒ y = 9/3 = 3
∴ Point of intersection = (-2, 3)
(i) In the line x + 2y - 5 = 0
⇒ 2y = - x + 5
⇒ y = -1/2 x + 5/2
∵ Slope (m₁) = -1/2
∴ Slope of its parallel line = -1/2
And equation of the parallel line y - y₁ = m(x - x₁)
⇒ y - 3 = -1/2 ×(x + 2)
⇒ 2y - 6 = -x - 2
⇒ x + 2y - 6 + 2 = 0
⇒ x + 2y - 4 = 0
(ii) ∵ Any line perpendicular to x-axis will be parallel to y - axis.
∴ Equation of the line will be
x = a
i.e., x = -2
⇒ x + 2 = 0
39. (i) Write down the co-ordinates of the point P that divides the line joining A (- 4, 1) and B (17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP where 0 is the origin
(iii) In what ratio does the y-axis divide the line AB?
Answer
(i) Co-ordinate A (-4, 1) and B (17, 10) P divides it in the ratio of 1 : 2
Let the co-ordinates of P will be (x, y)
∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)
= {1×17 + 2×(-4)}/(1+2)
= (17 - 8)/3
= 9/3
= 3
y = (m₁y₂ + m₂y₁)/(m₁ + m₂)
= (1×10 + 2×1)/(1 + 2)
= (10+2)/3
= 12/3
= 4
∴ Co-ordinates of P will be (3, 4)
(ii) O is the origin
∴ Distance between O and P

(iii) Let y-axis divides AB in the ratio of m₁ : m₂
∴ x = (m₁x₂ + m₂x₁)/(m₁+m₂)
⇒ 0 = {m₁×17 + m₂×(-4)}/(m₁+m₂)
⇒ 17m₁ - 4m₂ = 0
⇒ 17m₁ = 4m₂
⇒ m₁/m₂ = 4/17
⇒ m₁ : m₂ = 4 : 17
40. Find the image of the point (1, 2) in the line x - 2y - 7 = 0
Answer
Draw a perpendicular from the point P (1, 2) on the line, x - 2y - 7 = 0
Let P’ is the image of P and let its coordinates are (𝝰, 𝝱) slope of line x - 2y - 7 = 0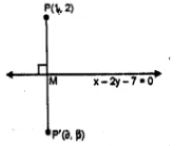


⇒ 2y = x - 7
⇒ y = 1/2 ×x - 7/2 is 1/2
∴ Slope of PP’ = -2 (∵ m₁m₂ = -1)
∴ Equation of PP’
y - y₁ = m(x - x₁) = y - 2 = -2×(x - 1)
⇒ y - 2 = -2x + 2
⇒ 2x + y = 2 + 2
⇒ 2x + y = 4
∵ P’ (𝝰, 𝝱) lies on it
∴ 2𝝰 + 𝝱 = 4 ...(i)
∵ P’ is the image of P in the line x - 2y - 7 = 0
∴ the lines bisects PP’ at M.
Or M is the mid-point of PP’
∴ Co-ordinates of M will be {(1+𝝰)/2, (2+𝝱)/2}
∵ M lies on the given line x - 2y - 7 = 0
∴ Substituting the value of x, y
(1+𝝰)/2 - {2(2 + 𝝱)/2} - 7 = 0
⇒ (1+𝝰)/2 - (2 + 𝝱) - 7 = 0
⇒ 1 + 𝝰 - 4 - 2𝝱 - 14 = 0
⇒ 𝝰 - 2𝝱 = 4 + 14 - 1 = 17 ...(ii)
⇒ 𝝰 = 17 + 2𝝱
Substituting the value of 𝝰 in (i)
2×(17 + 2𝝱) + 𝝱 = 4
34 + 4𝝱 + 𝝱 = 4
⇒ 5𝝱 = 4 - 34 = - 30
𝝱 = -30/5
= -6
Substituting the value of 𝝱 in (i)
2𝝰 - 6 = 4
⇒ 2𝝰 = 4 + 6 = 10
𝝰 = 10/2 = 5
∴ Co-ordinates of P’ will be (5, -6)
41. If the line x - 4y - 6 = 0 is the perpendicular bisector of the line segment PQ and the co-ordinates of P are (1, 3), find the co-ordinates of Q.
Answer
Let the co-ordinates of Q be (𝝰, 𝝱) and let the line x - 4y - 6 = 0 is the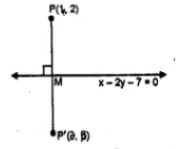


Perpendicular bisector of PQ and it intersects the line at M.
M is the mid point of PQ
Now slope of line x - 4y - 6 = 0
⇒ 4y = x - 6
⇒ y = 1/4 ×x - 6/4 is 1/4
∴ Slope of PQ = -4 (∵m₁m₂ = -1)
And equation of line PQ
y - y₁ = m(x - x₁)
⇒ y - 3 = -4 (x - 1)
⇒ y - 3 = -4x + 4
⇒ 4x + y - 3 - 4 = 0
⇒ 4x + y - 7 = 0
⇒ 4x + y = 7
∵ Q (𝝰, 𝝱) lies on it.
∴ 4𝝰 + 𝝱 = 7 ...(i)
Now co-ordinates of M will be {(1 + 𝝰)/2, (3 + 𝝱)/2}
∵ M lies on the line x - 4y - 6 = 0
∴ {(1 + 𝝰)/2 - 4(3+𝝱)/2} - 6 = 0
⇒ 1 + 𝝰 - 4(3 + 𝝱) - 12 = 0
⇒ 1 + 𝝰 - 12 - 4𝝱 - 12 = 0
⇒ 𝝰 - 4𝝱 = 24 - 1 = 23 ...(ii)
Multiply (i) by 4 and (ii) by 1
16𝝰 + 4𝝱 = 28
𝝰 - 4𝝱 = 23
Adding we get,
17𝝰 = 51
⇒ 𝝰 = 51/17 = 3
Substituting the value of 𝝰 in (i)
4×3 + 𝝱 = 7
⇒ 𝝱 = 7 - 12 = -5
∴ Co-ordinates of Q will be (3, -5).
Question 42: QABC is a square, O is the origin and the points A and B are (3, 0) and (p, q). If OABC lies in the first quadrant, find the values of p and q. Also write down the equations of AB and BC.
Answer


∵ OA = AB (sides of a square)


But OB² = OA² + AB²

⇒ p² + q² = 9 + (3 - p)² + q²
⇒ p² + q² = 9 + 9 + p² - 6p + q²
6p = 18
⇒ p = 18/6 = 3
Substituting the value of p in (i)
(3)² + q² - 6(3) = 0
⇒ 9 + q² - 18 = 0
⇒ q² - 9 = 0
⇒ q² = 9
⇒ q = 3
∴ p = 3, q = 3
∵ Equation AB will be x = 3
⇒ x - 3 = 0





Multiple Choice Questions





Choose the correct answer from the given four options :


1. The slope of a line parallel to y-axis is



(a) 0



(b) 1



(c) -1



(d) not defined



Answer


(d) not defined

Slope of a line parallel to y-axis is not defined.





2. The slope of a line which makes an angle of 30° with the positive direction of x-axis is



(a) 1



(b) 1/√3



(c) √3



(d) -1/√3



Answer


(b) 1/√3

Slope of a line which makes an angle of 30° with positive direction of x-axis = tan 30° =





3. The slope of the line passing through the points (0, -4) and (-6, 2) is



(a) 0



(b) 1



(c) -1



(d) 6



Answer


(c) -1

Slope of the line passing through the points (0, -4) and (-6, 2)

(y₂ - y₁)/(x₂ - x₁) = (2 + 4)/(- 6 - 0)

= 6/-6

= -1





4. The slope of the line passing through the points (3, - 2) and (- 7, - 2) is



(a) 0



(b) 1



(c) -1/10



(d) not defined.



Answer


(a) 0

Slope of the line passing through the points (3, -2) and (-7, 2)

(y₂ - y₁)/(x₂ - x₁) = (-2+2)/(-7-3)

= (0/-10)

= 0





5. The slope of the line passing through the points (3, -2) and (3, -4) is



(a) -2



(b) 0



(c) 1



(d) not defined



Answer


(d) not defined

Slope of the line passing through the points (3, -2) and (3, -4)

(y₂ - y₂)/(x₂ - x₁) = (-4+2)/(3 - 3)

= -2/0





6. The inclination of the line y = √3x - 5 is



(a) 30°



(b) 60°



(c) 45°



(d) 0°



Answer


(b) 60°

The inclination of the line y = √3x - 5 is √3 = tan 60°

= 60°





7. If the slope of the line passing through the points (2, 5) and (k, 3) is 2, then the value of k is



(a) -2



(b) -1



(c) 1



(d) 2



Answer


(c) 1

Slope of the line passing through (2, 5) and (k, 3) is 2, then

m = (y₂ - y₁)/(x₂ - x₁)

⇒ 2 = (3 - 5)/(k - 2)

⇒ 2 = (-2)/(k - 2)

⇒ 2k - 4 = -2

⇒ 2k = 4 - 2

= 2

⇒ k = 2/2 = 1





8. The slope of a line parallel to the line passing through the points (0, 6) and (7, 3) is



(a) -7/3



(b) -3/7



(c) -3



(d) 3



Answer


(b) -3/7

Slope of the line parallel to the line passing through (0, 6) and (7, 3)

Slope of the line = (y₂ - y₁)/(x₂ - x₁)

= (3 - 6)/(7 - 0)

= -3/7





9. The slope of a line perpendicular to the line passing through the points (2, 5) and (- 3, 6) is



(a) -1/5



(b) 1/5



(c) -5



(d) 5



Answer


(d) 5

Slope of the line joining the points (2, 5), (-3, 6)

= (y₂ - y₁)/(x₂ - x₁)

= (6 - 5)/(-3 - 2)

= 1/-5 = -1/5

∴ Slope of the line perpendicular to this line = 5





10. The slope of a line parallel to the line 2x + 3y - 7 = 0 is



(a) -2/3



(b) 2/3



(c) -3/2



(d) 3/2



Answer


(a) -2/3

The slope of a line parallel to the line 2x + 3y - 7 = 0

Slope of the line

3y = - 2x + 7

⇒ y = -2/3 + 7/3
= -2/3





11. The slope of a line perpendicular to the line 3x = 4y + 11 is



(a) 3/4



(b) -3/4



(c) 4/3



(d) -4/3



Answer


(d) -4/3

Slope of a line perpendicular to the line 3x = 4y + 11 is

⇒ 4y = 3x - 11

⇒ y = 3/4 x - 11/4

Slope = 3/4

∴ Slope of the line perpendicular to this line = -4/3 (∵ m × n = -1)





12. If the line 2x + 3y = 5 and kx - 6y = 7 are parallel, then the value of k is



(a) 4



(b) -4



(c) 1/4



(d) - 1/4



Answer


(b) -4

Lines 2x + 3y = 5 and kx - 6y = 7 are parallel

Slope of 2x + 3y = 5

Slope of kx - 6y = 7

⇒ 3y - 2x + 5

⇒ y = -2/3 ×x + 5/3

Slope of 2x + 3y = 5 is -2/3

And slope of kx - 6y = 7

6y = kx - 7

⇒ y = (k/6)×x - 7/6

∴ Slope = k/6

Since both lines are parallel

∴ -2/3 = k/6

⇒ k = (-2 × 6)/3

= -4





13. If the line 3x - 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other, then the value of k is



(a) 3/2



(b) -3/2



(c) 2/3



(d) -2/3



Answer


(a) 3/2

Line 3x - 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other

∴ Product of their slopes = (m₁×m₂) = -1

Slope of 3x - 4y + 7 = 0

⇒ 4y = 3x + 7

⇒ y = 3/4 x + 7/4

Slope (m₁) = 3/4

And slope of 2x + ky + 5 = 0

ky = -2x - 5

y = (-2/k) ×x - 5/k

∴ Slope (m₂) = -2/k

Since the given lines are perpendicular to each other

∴ 3/4 × -2/k = -1

⇒ -6/4k = -1

⇒ -k = -6/4
⇒ k = 3/2





Chapter Test





1. Find the equation of a line whose inclination is 60° and y-intercept is - 4.



Answer

Angle of inclination = 60°

Slope = tan θ

= tan 60°

= √3

Equation of the line will be,

y = mx + c

= √3x + (-4)

⇒ y - √3x - 4





2. Write down the gradient and the intercept on the y-axis of the line 3y + 2x = 12.



Answer

Slope of the line 3y + 2x = 12

⇒ 3y = 12 - 2x

⇒ 3y = - 2x + 12

⇒ y = (-2/3)×x + 4

∴ Slope = -2/3 and y-intercept = 4





3. If the equation of a line is y - √3x + 1, find its inclination.



Answer

In the line

y = √3x + 1

Slope = √3

⇒ tan θ = √3

⇒ θ = 60° (∵ tan 60° = √3)





4. If the line y = mx + c passes through the points (2, -4) and (-3, 1), determine the values of m and c.



Answer

The equation of line mx + c

∵ it passes through (2, -4) and (-3, 1)

Now substituting the value of these points -4 = 2m + c ...(i)

And 1 = -3m + c ...(ii)

Substracting we get,

-5 = 5m

⇒ m = -5/5 = -1

Substituting the value of m in (i)

-4 = 2(-1) + c

⇒ -4 = -2 + c

c = -4 + 2 = -2

∴ m = -1, c = -2





5. If the point (1, 4), (3, -2) and (p, - 5) lie on a straight line, find the value of p.



Answer

Let the points to be A (1, 4), B (3, -2) and C (p, -5) are collinear and let B (3, -2)

Divides AC in the ratio of m₁ : m₂

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

⇒ 3 = (m₁p + m₂×1)/(m₁ + m₂)

3m₁ + 3m₂ = m₁p + m₂

⇒ 3m₁ - m₁p = m₂ - 3m₂

⇒ m₁(3 - p) = -2 m₂

⇒ m₁/m₂ = - 2/(3 - p) ...(i)

and -2 = {m₁(-5) + m₂×4}/(m₁ + m₂)

⇒ -2m₁ - 2m₂ = - 5m₁ + 4m₂

⇒ -2m₁ + 5m₁ = 4 m₂ + 2m₂

⇒ 3m₁ = 6 m₂

⇒ m₁/m₂ = 6/3 = 2 ...(ii)

From (i) and (ii)

-2/(3-p) = 2

⇒ -2 = 6 - 2p

⇒ 2p = 6 + 2 = 8

⇒ p = 8/2 = 4





6. Find the inclination of the line joining the points P (4, 0) and Q (7, 3).



Answer

Slope of the line joining the points P (4, 0) and Q (7, 3)

= (y₂ - y₁)/(x₂ - x₁) = (3-0)/(7-4) = 3/3 = 1

∴ tan θ = 1

⇒ θ = 45° (∵ tan 45° = 1)

Hence inclination of line = 45°





7. Find the equation of the line passing through the point of intersection of the lines 2x + y = 5 and x - 2y = 5 and having y-intercept equal to -3/7.



Answer

Equation of lines are

2x + y = 5 ...(i)

x - 2y = 5 ...(ii)

Multiply (i) by 2 and (ii) by 1, we get

4x + 2y = 10

x - 2y = 5

Adding we get,

5x = 15

⇒ x = 15/5 = 3

Substituting the values of x in (i)

2×3 + y = 5

⇒ 6 + y = 5

⇒ y = 5 - 6

= -1

∴ Co-ordinates of point of intersection are (3, -1)

∵ the line passes through (3, -1)

∴ -1 = m×3 - 3/7 (y = mx + c)

3m = -1 + 3/7 = -4/7

m = -4/(7×3)

= -4/21

∴ Equation of line y = -4/21 ×x - 3/7

⇒ 21y = -4x - 9

⇒ 4x + 21y + 9 = 0





8. If point A is reflected in the y-axis, the co-ordinates of its image A₁, are (4, - 3).


(i) Find the co-ordinates of A.


(ii) Find the co-ordinates of A₂, A₃ the images of the points A, A₁, Respectively under reflection in the line x = - 2



Answer


(i) ∵ A is reflected in the y-axis and its image is A₁ (4, -3)

Co-ordinates of A will be (-4, 3)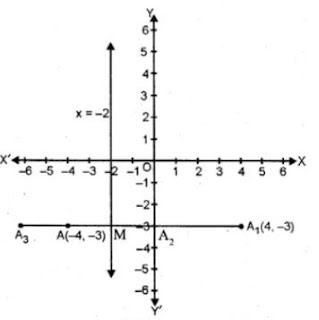



(ii) ∵ A₂ is the image of A (-4, -3) in the line

x = -2 which is parallel to y-axis

∴ AA₂ is perpendicular to the line x = -2 and this line bisects AA₂ at M.

Let co-ordinates of A₂ be (𝝰, 𝝱)

∴ 𝝰 = 0 and 𝝱 = -3

∴ Co-ordinates of A₂ will be (0, -3)

Again x = -2 is perpendicular bisector of A₁, A₃ intersecting it at M.

∴ M is mid point of A₁A₃.

∴ A₃M = MA₁
∴ Coordinates of A₃ will be (-8, -3)





9. If the lines x/3 + y/4 = 7 and 3x + ky = 11 are perpendicular to each other, find the value of k.



Answer

Given equation of lines are x/3 + y/4 = 7

⇒ 4x + 3y = 84

⇒ 3y = -4x + 84

⇒ y = -4/3 ×x + 28 ...(i)

And 3x + ky = 11

⇒ ky = -3x + 11

⇒ y = (-3/k)×x + 11/k ...(ii)

Let slope of line (i) be m₁ and of (ii) be m₂

∴ m₁ = -4/3 and m₂ = -(3/k)

∵ These lines are perpendicular to each other

∴ m₁m₂ = - 1

⇒ -4/3 × (-3/k) = -1

⇒ 4/k = -1

⇒ - k = 4

⇒ k = - 4





10. Write down the equation of a line parallel to x - 2y + 8 = 0 and passing through the point (1, 2).



Answer :

The equation of the line is x - 2y + 8 = 0

⇒ 2y = x + 8

⇒ y = (1/2)×x + 4

∴ Slope of the line = 1/2

∴ Slope of the line parallel to the given line passing through (1, 2) = 1/2

∴ Equation of the lines will be,

y - y₁ = m(x - x₁)

⇒ y - 2 = 1/2 (x - 1)

⇒ 2y - 4 = x - 1

⇒ x - 2y - 1 + 4 = 0

⇒ x - 2y + 3 = 0





11. Write down the equation of the line passing through (-3, 2) and perpendicular to the line 3y = 5 - x.



Answer

Equation of the line is

3y = 5 - x

⇒ 3y = -x + 5

⇒ y = -(1/3)×x + 5/3

∴ Slope of the line = -1/3

And slope of the line perpendicular to it and passing through (-3, 2) will be = 3

(∵ m₁m₂ = -1)

∴ Equation of the line will be

y - y₁ = m(x - x₁)

⇒ y - 2 = 3(x + 3)

⇒ y - 2 = 3x + 9

⇒ 3x - y + 9 + 2 = 0

⇒ 3x - y + 11 = 0





12. Find the equation of the line perpendicular to the line joining the points A (1, 2) and B (6, 7) and passing through the point which divides the line segment AB in the ratio 3 : 2.



Answer

Let slope of the line joining the points A (1, 2) and B (6, 7) be m₁

∴ m₁ = (y₂ - y₁)/(x₂ - x₁)

= (7-2)/(6-1)

= 5/5

= 1

Let m₂ be the slope of the line perpendicular to it then m₁×m₂ = -1

⇒ 1×m₂ = -1

∴ m₂ = -1

Let the point P (x, y) divides the line AB in the ratio of 3 : 2

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {3×6 + 2×1)/(3 + 2)

= (18+2)/5

= 20/5

= 4

And y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= (3×7 + 2×2)/(3+2)

= (21+4)/5

= 25/5

= 5

∴ Co-ordinates of P will be (4, 5)

Now equation of the line passing through P and having slope -1

y - y₁ = m(x - x₁)

⇒ y - 5 = -1(x - 4)

⇒ y - 5 = -x + 4

⇒ x + y - 5 - 4 = 0
⇒ x + y - 9 = 0





13. The points A (7, 3) and C (0, -4) are two opposite vertices of a rhombus ABCD. Find the equation of the diagonal BD.



Answer

Slope of line AC (m₁)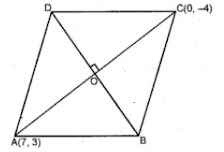


= (y₂ - y₁)/(x₂ - x₁)

= (-4 - 3)/(0 - 7)

= -7/-7

= 1

∵ Diagonals of a rhombus bisect each other at right angles

∴ BD is perpendicular to AC

∴ Slope of BD = -1 (∵ m₁m₂ = -1)

And co-ordinates of O, the mid-point of AC will be {(7 + 0)/2, (3 - 4)/2} or (7/2, -1/2)

∴ Equation of BD will be

y - y₁ = m(x - x₁)

⇒ y + 1/2 = -1 (x - 7/2)

⇒ y + 1/2 = -x + 7/2

⇒ 2y + 1 = -2x + 7

⇒ 2x + 2y + 1 - 7 = 0

⇒ 2x + 2y - 6 = 0

⇒ x + y - 3 = 0 (Dividing by 2)





14. A straight line passes through P (2, 1) and cuts the axes in points A, B. If BP : PA = 3 : 1, find :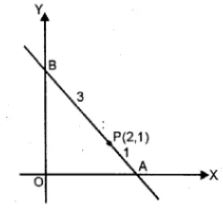





(i) the co-ordinates of A and B.


(ii) the equation of the line AB



Answer

(i) A lies on x-axis and B lies on y-axis

Let co-ordinates of A be (x, 0) and B be (0, y) and P (2, 1) divides BA in the ratio 3:1.

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

⇒ 2 = (3×x + 1×0)/(3+1)

⇒ 3x/4 = 2

⇒ 3x = 8

⇒ x = 8/3

And y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

⇒ 1 = (3×0 + 1×y)/(3+1)

⇒ y/4 = 1

⇒ y = 4

∴ Co-ordinates of A will be (8/3, 0) and of B will be (0, 4)

(ii) Slope of the line AB = (y₂ - y₁)/(x₂ - x₁)

= (4 - 0)/(0 - 8/3)

= {4/(-8/3)}

= - 4 × 3/8

= -3/2

∴ Equation of AB will be

y - y₁ = m(x - x₁)

⇒ y - 1 = -3/2 (x - 2)

⇒ 2y - 2 = -3x + 6

⇒ 3x + 2y - 2 - 6 = 0

⇒ 3x + 2y - 8 = 0





15. A straight line makes on the co-ordinates axes positive intercepts whose sum is 7. If the lines passes through the point (-3, 8), find its equation.



Answer

Let the line make intercept a and b with the x-axis and y-axis respectively then the line passes through


A (a, 0) and B (0, b)

But a + b = 7

b = 7 - a

Now slope of the line = (y₂ - y₁)/(x₂ - x₁)

= (b - 0)/(0 - a)

= -b/a

∴ Equation of the line y - y₁ = m(x - x₁)

⇒ y - 0 = (-b/a).(x - a) ...(i)

∵ the line passes through the point (-3, 8)

∴ 8 - 0 = -b/a(- 3 - a)

= - {(7 - a)/a}×(-3 - a)

⇒ 8a = (7 - a)(3 + a)

⇒ 8a = 21 + 7a - 3a + a²

⇒ a² + 8a - 7a + 3a - 21 = 0

⇒ a² + 4a - 21 = 0

⇒ a² + 7a - 3a - 21 = 0

⇒ a(a + 7) - 3(a + 7) = 0

⇒ (a + 7)(a - 3) = 0

Either a + 7 = 0, then a = -7, which is not possible as it is not positive

Or a - 3 = 0, then a = 3

and b = 7 - 3 = 4

∴ Equation of the line y - 0 = -(b/a)×(x - a)

⇒ y = -4/3(x - 3)

⇒ 3y = -4x + 12

⇒ 4x + 3y - 12 = 0
⇒ 4x + 3y = 12






16. If the coordinates of the vertex A of a square ABCD are (3, - 2) and the equation of diagonal BD is 3x - 7y + 6 = 0, find the equation of the diagonal AC. Also find the co-ordinates of the center of the square.



Answer :

Co-ordinates of A are (3, - 2)



Diagonals AC and BD of the square ABCD bisect each other at right angle at O.

∴ O is the mid-point of AC and BD equation

Diagonals AC and BD of the square ABCD bisect each other at right angle at O.

∴ O is mid-point of AC and BD

Equation of BD is 3x - 7y + 6 = 0

⇒ 7y = 3x + 6

⇒ y = (3/7)×x + 6/7

∴ Slope of BD = 3/7

And slope of AC = -7/3 (∵ m₁m₂ = -1)

∴ Equation of AC will be

y - y₁ = m(x - x₁)

⇒ y + 2 = -7/3 (x - 3)

⇒ 3y + 6 = -7x + 21

⇒ 7x + 3y + 6 - 21 = 0

⇒ 7x + 3y - 15 = 0

Now we will find the co-ordinates of O, the points of intersection of AC and BD

We will solve the equations,

3x - 7y = - 6 ...(i)

7x + 3y = 15 ...(ii)

Multiplying (i) by 3 and (ii) by 7, we get,

9x - 21y = - 18 ...(iii)

49x + 21y = 105 ...(iv)

Adding we get,

58x = 87

⇒ x = 87/58 = 3/2

Substituting the value of x in (iii)

9(3/2) - 21y = - 18

⇒ 27/2 - 21y = - 18

21y = 27/2 + 18

= (27 + 36)/2

= 63/2

y = 63/(2×21)

= 3/2
∴ Co-ordinates of O will be (3/2, 3/2)

•