1. Find the remainder (without divisions) on dividing f(x) by x - 2, where
(i) f(x) = 5x² - 1x + 4
(ii) f(x) = 2x³ - 7x² + 3
Answer
Let x - 2 = 0, then x = 2
(i) Substituting value of x in f(x)
f(x) = 5x² - 7x + 4
⇒ f(2) = 5(2)² - 7(2) + 4
⇒ f(2) = 20 - 14 + 4 = 10
Hence Remainder = 10
(ii) f(x) = 2x³ - 7x² + 3
∴ f(2) = 2(2)³ - 7(2)² + 3
= 16 - 28 + 3
Hence remainder = - 9
2. using remainder theorem, find the remainder on dividing f(x) by (x + 3) where
(i) f(x) = 2x² - 5x + 1
(ii) f(x) = 3x³ + 7x² - 5x + 1
Answer
Let x + 3 = 0
⇒ x = - 3
Substituting the value of x in f(x),
(i) f(x) = 2x² - 5x + 1
∴ f(-3) = 2(-3)² - 5(-3) + 1
= 18 + 15 + 1
= 34
Hence Remainder = 34
(ii) f(x) = 3x³ + 7x² - 5x + 1
= 3(-3)³ + 7(-3)² - 5(-3) + 1
= - 81 + 63 + 15 + 1
= - 2
Hence Remainder = - 2
3. Find the remainder (without division) on dividing f(x) by (2x + 1) where
(i) f(x) = 4x² + 5x + 3
(ii) f(x) = 3x² - 7x² + 4x + 11
Answer
Let 2x + 1 = 0, then x = - (1/2)
Substituting the value of x in f(x):
(i) f(x) = 4x² + 5x + 3
= 4(- 1/2)² + 5 × (-1/2) + 3
= 4 × 1/4 - 5/2 +3
= 1 - 5/2 + 3
= 4 - 5/2
= 3/2
∴ Remainder = 3/2
(ii) f(x) = 3x³ - 7x² + 4x + 11
= - 3(- 1/2)³ - 7(- 1/2)² + 4(- 1/2) + 11
= 3(- 1/8) - 7(1/4) + 4(- 1/2) + 11
= - 3/8 - 7/4 - 2 + 11
= (- 3 - 14 - 16 + 88)/8
= 55/8
= 6.7/8
4. (i) Find the remainder (without division) when 2x³ - 3x² + 7x - 8 is divided by x - 1
(ii) Find the remainder (without division) on dividing 3x² + 5x - 9 by (3x + 2)
Answer
(i) Let x - 1 = 0, then x = 1
Substituting value of x in f(x)
f(x) = 2x³ - 3x² + 7x - 8
= 2(1)³ - 3(1)² + 7(1) - 8
= 2 × 1 - 3 × 1 + 7 × 1 - 8
= 2 - 3 + 7 - 8
= - 2
∴ Remainder = 2
(ii) Let 3x + 2 = 0, then 3x = - 2
⇒ x = -2/3
Substituting the value of x in f(x)
f(x) = 3x² + 5x - 9
= 3(-2/3)² + 5{-(2/3)} - 9
= 3 × 4/9 - 5 × 2/3 - 9
= 4/3 - 10/3 - 9
= - 6/3 - 9
= - 2 - 9
= - 11
∴ Remainder = - 11





5. Using remainder theorem, find the value of k if on dividing 2x²
+ 3x²
- kx + 5 by x - 2, leaves a remainder 7.



Answer

f(x) = 2x² + 3x² - kx + 5

g(x) = x - 2, if x - 2 = 0, then x = 2

Dividing f(x) by g(x) the remainder will be

f(2) = 2(2)³ + 3(2)² - k × 2 + 5

= 16 + 12 - 2k + 5

= 33 - 2k

Remainder = 7

∴ 33 - 2k = 0

⇒ 33 - 7 = 2k

⇒ 2k = 26

⇒ k = 26/2 = 13

∴ k = 13




6. Using remainder theorem, find the value of a if the division of x³ + 5x² - ax + 6 by (x - 1) leaves the remainder 2a.



Answer

Let x - 1 = 0, then x = 1

Substituting the value of x in f(x)

f(x) = x³ + 5x² - ax + 6

= (1)3 + 5(1)² - a(1) + 6

= 1 + 5 - a + 6

= 12 - a

∵ Remainder = 2a

∴ 12 - a = 2a

⇒ 12 = a + 2a

⇒ 3a = 12

∴ a = 4





7. (i) What number must be subtracted from 2x² - 5x so that the resulting polynomial leaves the remainder 2, when divided by 2x + 1 ?


(ii) What number must be added to 2x³ - 7x² + 2x so that the resulting polynomial leaves the remainder - 2 when divided by 2x - 3?



Answer


(i) Let a be subtracted from 2x² - 5x,

Dividing 2x² - 5x by 2x + 1,


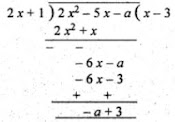
Here remainder is (3 - a) but we are given that remainder is 2.

∴ 3 - a = 2

⇒ - a = 2 - 3 = - 1

⇒ a = 1

Hence, 1 is to be subtracted.
(ii) Let a be added to 2x³ - 7x² + 2x dividing by 2x - 3, then


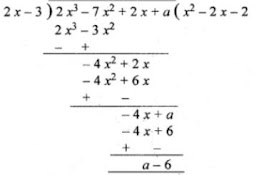
But remainder is - 2, then
a - 6 = - 2
⇒ a = - 2 + 6
⇒ a = 4
Hence, 4 is to be added.
8. (i) When divided by x - 3 the polynomials x² - px² + x + 6 and 2x³ - x² - (p + 3)x - 6 leave the same remainder. Find the value of ‘p’
(ii) Find ‘a’ if the two polynomials ax³ + 3x² - 9 and 2x³ + 4x + a, leaves the same remainder when divided by x + 3.
Answer
(i) By dividing x³ - px² + x + 6
And 2x³ - x² - (p + 3)x - 6
By x - 3, the remainder is same Let x - 3 = 0, then x = 3
Now by Remainder Theorem,
Let p(x) = x³ - px² + x + 6
p(3) = (3)³ - p(3)² + 3 + 6
= 27 - 9p + 9
= 36 - 9p
and q(x) = 2x³ - x² - (p + 3)x - 6
q(3) = 2(3)² - (3)² - (p + 3) × 3 - 6
= 2 × 27 - 9 - 3p - 9 - 6
= 54 - 24 - 3p - 9 - 6
= 54 - 24 - 3p
= 30 - 3p
∵ The remainder in each case is same
∴ 36 - 9p = 30 - 3p
36 - 30 = 9p - 3p
⇒ 6 = 6p
⇒ p = 6/6 = 1
∴ p = 1
(ii) Find ‘a’ if the two polynomials ax³ + 3x² - 9 and 2x³ + 4x + a, leaves the same remainder when divided by x + 3.
The given polynomials are ax³ + 3x² - 9 and 2x³ + 4x + a
Let p(x) = ax³ + 3x² - 9
and q(x)= 2x3 + 4x + a
Given that p(x) and q(x) leave the same remainder when divided by (x + 3),
Thus by Remainder Theorem, we have
p(-3) = q(-3)
⇒ a(-3)³ + 3(-3)² - 9 = 2(-3)³ + 4(-3) + a
⇒- 27a + 27 - 9 = - 54 - 12 + a
⇒ - 27a - a = - 66 - 18
⇒ - 28a = - 84
⇒ a = 84/28
∴ a = 3
9. By factor theorem show that (x + 3) and (2x - 1) are factors of 2x²
+ 5x - 3.
Answer
Let x + 3 = 0 then x = - 3
Substituting the value of x in f(x)
f(x) = 2x² + 5x - 3 = 2(- 3)² + 5(- 3) - 3
f(- 3) = 18 - 15 - 3 = 0
∵ Remainder = 0, then x + 3 is a factor
Again let 2x - 1 = 0, then x = 1/2
Substituting the value of x in f(x),
f(x) = 2x² + 5x - 3
f(1/2) = 2(1/2)² + 5(1/2) - 3
= 2 × 1/4 + 5/2 - 3
= 1/2 + 5/2 - 3 = 0
∵ Remainder = 0,
∴ 2x - 1 is also a factor
Hence, proved
10. Without actual division, prove that x⁴ + 2x³ - 2x² + 2x - 3 is exactly divisible by x² + 2x - 3.
Answer
x² + 2x - 3
= x² + 3x - x - 3
= x(x + 3) - 1(x + 3)
= (x + 3)(x - 1)
Let p(x) = x⁴ + 2x³ - 2x² + 2x - 3
We see that
p(-3) = (- 3)⁴ + 2(- 3)³ - 2(-3)² + 2(-3) - 3
= 81 - 54 - 18 - 6 - 3
= 0
Hence by converse of factor theorem, (x + 3) is a factor of p(x).
Also we see that
p(1) = (1)⁴ + 2(1)³ - 2(1)² + 2(1) - 3 = 0
Hence by converse of factor theorem, (x - 1) is a factor of p(x).
From above, we see that
(x + 3)(x - 1), i.e., x² + 2x - 3 is a factor of p(x)
⇒ p(x) is exactly divisible by (x² + 2x - 3)
11. Show that (x - 2) is a factor of 3x² - x - 10. Hence factorise 3x² - x - 10.
Answer
Let x - 2 = 0, then x = 2
Substituting the value of x in f(x),
f(x) = 3x² - x - 10
= 3(2)² - 2 - 10
= 12 - 2 - 10 = 0
∵ Remainder is zero
∴ x - 2 is a factor of f(x).
Dividing 3x² - x - 10 by x - 2, we get


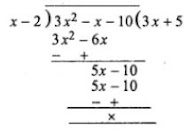
∴ 3x² - x - 10 = (x - 2)(3x + 5)





12. (i) Show that (x - 1) is a factor of x³ - 5x² - x + 5. Hence, factorise x³ - 5x² - x + 5.


(ii) Show that (x - 3) is a factor of x³ - 7x² + 15x - 9. Hence, factorise x³ - 7x² + 15x - 9



Answer

(i) Let x - 1 = 0, then x = 1

Substituting the value of x in f(x),

f(x) = x³ - 5x² - x + 5

= (1)³ - 5(1)² - 1 + 5

= 1 - 5 - 1 + 5

= 0

∵ Remainder = 0

∴ x - 1 is a factor of x³ - 5x² - x + 5

Now dividing f(x) by x - 1, we get




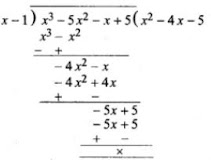
∴ x³ - 4x² - x + 5

= (x - 1)(x² - 4x - 5) = (x - 1)[x² - 5x + x - 5]

= (x - 1)[x(x - 5) + 1(x - 5)]

= (x - 1)(x + 1)(x - 5)

(ii) Let x - 3 = 0, then x = 3,

Substituting the value of x in f(x), f(x) = x3 - 7x2 + 15x - 9

= (3)³ - 7(3)² + 15(3) - 9

= 27 - 63 + 45 - 9

= 72 - 72

= 0

∵ Remainder = 0,

∴ x - 3 is a factor of x³ - 7x² + 15x - 9

Now dividing it by x - 3, we get


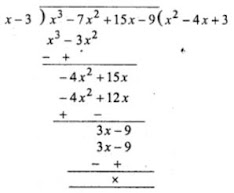
∴ x³ - 7x² + 15x - 9

= (x - 3)(x² - 4x + 3) = (x - 3)[x² - x - 3x + 3]

= (x - 3)[x(x - 1) - 3(x - 1)]
= (x - 3)(x - 1)(x - 3) = (x - 3)²(x - 1)





13. Show that (2x + 1) is a factor of 4x³
+ 12x²
+ 11x + 3. Hence factorise 4x³
+ 12x³
+ 11x + 3.



Answer

Let 2x + 1 = 0,

Then x = - 1/2

Substituting the value of x in f(x),

f(x) = 4x³ + 12x² + 11x + 3

f(-1/2) = 4(-1/2)³ + 12(-1/2)² + 11(-1/2) + 3

= 4(- 1/8)

= - 1/2 + 3 - 11/2 + 3

= (6) - (6) = 0

∵ Remainder = 0,

∴ 2x + 1 is a factor of

4x³ + 12x² + 11x + 3

Now dividing f(x) by 2x + 1, we get


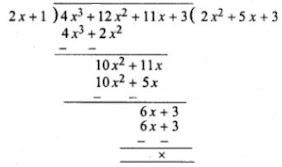
∴ 4x³ + 12x² + 11x + 3

= (2x + 1)(2x² + 5x + 3)

= (2x + 1)[2x² + 2x + 3x + 3]

(2x + 1)[2x(x + 1) + 3(x + 1)]

= (2x + 1)[(x + 1)(2x + 3)]

= (2x + 1)(x + 1)(2x + 3)





14. Show that 2x + 7 is a factor of 2x³
+ 5x²
- 11x - 14. Hence factorise the given expression completely, using the factor theorem.



Answer

Let 2x + 7 = 0, then 2x = - 7

x = (-7)/2

Substituting the value of x in f(x),

f(x) = 2x³ + 5x² - 11x - 14

f(- 7/2) = 2(- 7/2)³ + 5(-7/2)² - 11(- 7/2) - 14

= (-343)/4 + 245/4 + 77/2 - 14

= (- 343 = 245 + 154 - 56)/4

= (- 399 + 399)/4

= 0

Hence, (2x + 7) is a factor of f(x).

Now, 2x³ + 5x² - 11x - 14 = (2x + 7)(x² - x - 2)

= (2x + 7)[x² - 2x + x - 2]

= (2x + 7)[x(x - 2) + 1(x - 2)]
= (2x + 7)(x + 1)(x - 2)




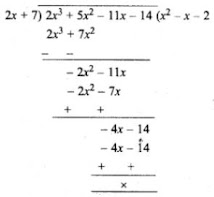
15. Use factor theorem to factorise the following polynomials completely.
(i) x³ + 2x² - 5x - 6
(ii) x³ - 13x - 12
Answer
(i) Let f(x) = x³ + 2x² - 5x - 6
Factors of (∵ 6 = ± 1; ± 2, ± 3, ± 6)
Let x = - 1, then
f(-1) = (-1)³ + 2(-1)² - 5(-1) - 6
= - 1 + 2(1) + 5 - 6
= - 1 + 2 + 5 - 6
= 7 - 7
= 0
∵ f(-1) = 0
∴ x + 1 is a factor of f(x)
Now, dividing f(x) by x + 1, we get
f(x) = (x + 1) (x² + x - 6)
= (x + 1)(x² + 3x - 2x - 6)
= (x + 1){x(x + 3) - 2(x + 3)}
= (x + 1)(x + 3)(x - 2)


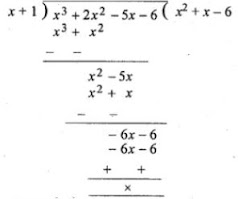
(ii) f(x) = x³ - 13x - 12
Let x = 4, then
f(x) = (4)³ - 13(4) - 12
= 64 - 52 - 12
= 64 - 64 = 0
∵ f(x) = 0
∴ x - 4 is a factor of f(x).
Now dividing f(x) by (x - 4), we get,
f(x) = (x - 4)(x² + 4x + 3)
= (x - 4)(x² + 3x + x + 3)
= (x - 4)[x(x + 3) + 1(x + 3)]


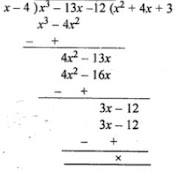
Question 16: Use the remainder Theorem to factorise the following expression
(i) 2x³ + x² - 13x + 6.
(ii) 3x² + 2x² - 19x + 6
(iii) 2x³ + 3x² - 9x - 10
Answer
(i) Let f(x) = 2x³ + x² - 13x + 6
Factors of 6 are ±1, ±2, ±3, ±6
Let x = 2, then
f(2) = 2(2)³ + (2)² - 13 × 2 + 6
= 16 + 4 - 26 + 6
= 26 - 26
= 0
∵ f(2) = 0
∴ x - 2 is the factor of f(x) (By Remainder Theorem)
Dividing f(x) by x - 2, we get


∴ f(x) = (x - 2)(2x² + 5x - 3)
= (x - 2){2x² + 6x - x - 3}
= (x - 2){2x(x + 3) - 1(x + 3)}
= (x - 2)(x + 3)(2x - 1)
(ii) P(x) = 3x³ + 2x² - 19x + 6
P(1) = 3 + 2 - 19 + 6
= - 8 ≠ 0
P(-1)= - 3 + 2 + 19 + 6
= - 24 ≠ 0
P(2) = 24 + 8 - 38 + 6 = 0
Hence, (x - 2) is a factor of p(x)
∴ P(x) = 3x³ + 2x² - 19x + 6
= 3x³ - 6x² + 8x² - 16x - 3x + 6
= 3x²(x - 2) + 8x(x - 2) - 3(x - 2)
= (x - 2)(3x² + 8x - 3)
= (x - 2)(3x² + 9x - x - 3)
= (x - 2){3x(x + 3) - 1(x + 3)
= (x - 2)(x + 3)(3x - 1)
(iii) f(x) = 2x³ + 3x² - 9x - 10
f(-1) = 2(-1)³ + 3(-1)² - 9(-1) - 10
∴ f(-1) = - 2 + 3 + 9 - 10 = 0


∴ (x + 1) is a factor.
∴ 2x² + x - 10 = 2x² + 5x - 4x - 10
= x(2x + 5) - 2(2x + 5) - (2x + 5)(x - 2)
∴ factors are (x + 1) (x - 2)(2x + 5)





17. Using the Remainder and factor Theorem, factorise the following polynomial:
x³ + 10x² - 37x + 26.
Answer
f(x) = x³ + 10x² - 37x + 26
f(1) = (1)³ + 10(1)² - 37(1) + 26
= 1 + 10 - 37 + 26
= 0
x = 1


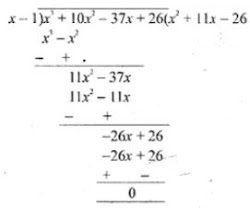
x - 1 is factor of f(x)
∴ f(x) = (x - 1)(x² + 11x - 26)
= (x - 1)(x² + 13x - 2x - 26)
= (x - 1)[x(x + 13) - 2(x + 13)]
= (x - 1)[(x - 2)(x + 13)]





18. If (2x + 1) is a factor of 6x³ + 5x² + ax - 2. Find the value of a.
Answer
Let 2x + 1 = 0, then x = - (1/2)
Substituting the value of x in f(x),
f(x) = 6x³ + 5x² + ax - 2
f(-1/2) = 6(- 1/2)³ + 5(- 1/2)² + a(-1/2) - 2
= 6(-1/8) + 5(1/4) + a(- 1/2) - 2
= - 3/4 + 5/4 - a/2 - 2
= (-3 + 5 - 2a - 8)/4
= (- 6 - 2a)/4
∵ 2x + 1 is a factor of f(x)
∴ Remainder = 0
∴ (- 6 - 2a)/4 = 0
⇒ - 6 - 2a = 0
⇒ 2a = - 6
⇒ a = - 3
∴ a = - 3
19. If (3x - 2) is a factor of 3x³ - kx² + 21x - 10, find the value of k.
Answer
Let 3x - 2 = 0, then 3x = 2
⇒ x = 2/3
Substituting the value of x in f(x),
f(x) = 3x³ - kx² + 21x - 10
f(2/3) = 3(2/3)³ - k(2/3)² + 21(2/3) - 10
= 3 × 8/27 - k × 4/9 + 21 × 2/3 - 10
= 8/9 - 4k/9 + 14 - 10
= (8 - 4k)/9 + 4
∵ Remainder is 0
∴ (8 - 4k)/9 + 4 = 0
⇒ 8 - 4k + 36 = 0
⇒ - 4k + 44 = 0
⇒ 4k = 44
∴ k = 11
20. If ( x - 2) is a factor of 2x³ -x² + px - 2, then
(i) find the value of p.
(ii) with this value of p, factorize the above expression completely
Answer
(i) Let x - 2 = 0, then x = 2
Now f(x) = 2x³ - x² + px - 2
∴ f(2) = 2(3)³ - (2)² + p × 2 - 2
= 2 × 8 - 4 + 2p - 2
= 16 - 4 + 2p - 2 = 10 + 2p
(ii) ∴ f(2) = 0, then 10 + 2p = 0
⇒ 2p = -10
⇒ p = -5
Now, the polynomial will be
2x³ - x² - 5x - 2
= (x - 2)(2x² + 3x + 1)
= (x - 2)[2x² + 2x + x + 1]
= (x - 2)[2x(x + 1) + 1(x + 1)]
= (x - 2)(x + 1)(2x + 1)


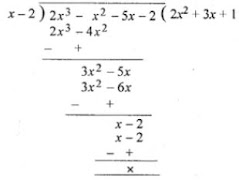
21. Find the value of ‘K’ for which x = 3 is a solution of the quadratic equation, (k + 2)x² - Kx + 6 = 0.
Also, find the other root of the equation.
Answer
(K + 2)x² - Kx + 6 = 0 ...(1)
Substitute x = 3 in equation (1)
(- 4 + 2)x² - (- 4)x + 6 = 0
⇒ - 2x² + 4x + 6 = 0
⇒ x² - 2x - 3 = 0 (Dividing by 2)
⇒ x³ - 3x + x - 3 = 0
⇒ x² - 3x + x - 3 = 0
⇒ x(x - 3) + 1(x - 3) = 0
⇒ (x + 1)(x - 3) = 0
So, the roots are x = - 1and x = 3
Thus, the other root of the equation is x = - 1
22. What number should be subtracted from 2x³ - 5x² + 5x so that the resulting polynomial has 2x - 3 as a factor?
Answer

Let the number to be subtracted be k and the resulting polynomial be f(x), then
f(x) = 2x³ - 5x² + 5x - k
Since, 2x - 3 is a factor of f(x),
Now, converting 2x - 3 to factor theorem
f(3/2) = 0
⇒ 2x³ - 5x² + 5x - k = 0
⇒ 2(3/2)³ - 5(3/2)² + 5(3/2) - k = 0
⇒ 2 × 27/8 - 5 × 9/4 + 5 × 3/2 - k = 0
⇒ 27/4 - 45/4 + 15/2 - k = 0
⇒ 27 - 45 + 30 - 4k = 0
⇒ - 4k + 12 = 0
⇒ k = - 12/-4
⇒ k = 3
23. (i) Find the value of the constant a and b, if (x - 2) and (x + 3) are both factors of the expression x³ + ax² + bx - 12.
(ii) If (x + 2) and (x + 3) are factors of x³ + ax + b, Find the values of a and b.
Answer

Let x - 2 = 0, then x = 0
Substituting value of x in f(x)
f(x) = x³ + ax² + bx - 12
f(2) = (2)³ + a(2)² + b(2) - 12
= 8 + 4a + 2b - 12
= 4a + 2b - 4
∵ x - 2 is a factor
∴ 4a + 2b - 4 = 0
⇒ 4a + 2b = 4
⇒ 2a + b = 2
Again let x + 3 = 0, then x = - 3
Substituting the value of x in f(x)
f(x) = x³ + ax² + bx - 12
= (-3)³ + a(-3)² + b(-3) - 12
⇒ - 27 + 9x - 3b - 12
= - 39 + 9a - 3b
∵ x + 3 is a factor of f(x)
∴ - 39 + 9a - 3b = 0
⇒ 9a - 3b = 39
⇒ 3a - b = 13 ....(ii)
Adding (i) and (ii)
5a = 15
⇒ a = 3
Substituting the value of a in (i)
2(3) + b = 2
⇒ 6 + b = 2
⇒ b = 2 - 6
∴ b = - 4
Hence a = 3, b = - 4
(ii) Since (x + 2) = 0
f(x) = x³ + ax + b
f(-2) = (-2)³ + a(-2) + b
Since x + 2 is a factor, by factor theorem
- 8 - 2a + b = 0
∴ - 2a + b = 8 .....(i)
Since x + 3 = 0
∴ x = - 3
f(x) = x³ + ax + b
∴ f(-3) = (-3)³ + a(-3) + b
∴ f(-3) = - 27 - 3a + b
By factor theorem, - 27 - 3a + b = 0
∴ - 3a + b = 27 ....(ii)
Subtracting eq. (ii) from eq. (i)
- 2a + b = 8
- 3a + b = 27
a = - 19
Now, substituting the value of a in eq. (i)
- 2(- 19) + b = 8
⇒ 38 + b = 8
b = - 30
dlt28231083636114642732">
24. If (x + 2) and (x - 3) are factors of x³ + ax + b, find the values of a and b, With these values of a and b, factorize the given expression.
Answer
Let x + 2 = 0, then x = - 2
Substituting the value of x in f(x),
f(x) = x³ + ax + b
f(-2) = (-2)³ + a(-2) + b
= - 8 - 2a + b
∵ x + 2 is a factor
∴ Remainder is zero.
∴ - 8 - 2a + b = 0
⇒ - 2a + b = 8
∴ 2a - b = - 8 ...(i)
Again let x - 3 = 0, then x = 3, Substituting the value of x in f(x),
f(x) = x³ + ax +b
f(3) = (3)³ + a(3) + b
= 27 + 3a + b
∵ x - 3 is a factor
∴ Remainder = 0
⇒ 27 + 3a + b = 0
⇒ 3a + b = - 27 ...(ii)
Adding (i) and (ii)
5a = - 35
⇒ a = - 35/5
= - 7
Substituting value of a in (i)
2(-7) - b = - 8
∴ - 14 - b = - 8
- b = - 8 + 14
⇒ - b = 6
∴ b = - 6
Hence a= - 7, b = - 6
(x + 2) and (x - 3) are the factors of x² + ax + b
x³ + ax + b ⇒ x³ + 7x - 6
Now dividing x³ - 7x - 6
Now dividing x³ - 7x - 6 by (x + 2)
(x - 3) or x² - x - 6, we get


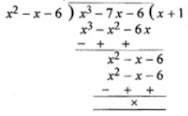
∴ Factors are (x + 2), (x - 3) and (x + 1)





25. (x - 2) is a factor of the expression x³ + ax² + bx + 6. When this expression is divided by (x - 3), it leaves the remainder 3. Find the values of a and b.



Answer

As, x - 2 is a factor of

f(x) = x³ + ax² + bx + 6

∴ f(2) = 0

∴ (2)³ + a(2)² + b(2) + 6 = 0

⇒ 8 + 4a + 2b + 6 = 0

⇒ 4a + 2b = - 14

⇒ 2a + b = - 7 ...(i)

As on dividing f(x) by x - 3

Remainder = 3

∴ f(3) = 3

∴ (3)³ + a(3)² + b(3) + 6 = 3

⇒ 27 + 9a + 3b + 6 = 3

⇒ 9a + 3b = - 30

⇒ 3a + b = - 10 ...(ii)

Solving simultaneously equation (i) and (ii),

∴ 2a + b = - 7

3a + b = - 10

Subtracting,

- a = 3

a = - 3

Substituting value of a in equation (i)

2(-3) + b = - 7

∴ 6 + b = - 7

∴ b = - 1

∴ a = - 3, b = - 1





26. If (x - 2) is a factor of the expression 2x³ + ax² + bx - 14 and when the expression is divide by (x - 3), it leaves a remainder 52, find the values of a and b.



Answer

f(x) = 2x³ + ax² +bx - 14

∴ (x - 2) is factor of f(x)

f(2) = 0

2(2)³ + a(2)² + b(2) - 14 = 0

16 + 4a + 2b - 14 = 0

⇒ 4a + 2b = - 2

2a + b = - 1 ....(i)

Also, (x - 3) it leaves remainder = 52

∴ f(3) = 52

2(3)³ + a(3)² + b(3) - 14 = 52

⇒ 54 + 9a + 3b - 14 = 52

⇒ 9a + 3b = 52 - 40

9a + 3b = 12

3a + b = 4 ...(ii)

From (i) and (ii)

2a + b = - 1

3a + b = 4

Subtracting - a = - 5

∴ a = 5 put in (i)

∴ 2(5) + b = - 1

⇒ b = - 1 - 10

⇒ b = - 11

∴ a = 5, b = - 11

⇒ - 27a/8 + 27/4 - 3b/2 - 3 = 0

⇒ - 27a + 54 - 12b - 24 = 0 (Multiplying by 8)

⇒ - 27a - 12b + 30 = 0

⇒ - 27 a - 12b = - 30

⇒ 9a + 4b = 10 [Dividing by (-3)]

9a + 4b = 10 .....(i)

Again let x + 2 = 0 then x = - 2

Substituting the value of x in f(x)

f(x) = ax³ + 3x² + bx - 3

f(-2) = a(-2)³ + 3(-2)² + b(-2) - 3

= - 8a + 12 - 2b - 3

= - 8a - 2b + 9

∵ Remainder = - 3

∴ - 8a - 2b + 9 = - 3

⇒ - 8a - 2b = - 3 - 9

⇒ - 8a -2b = - 12 (Dividing by 2)

⇒ 4a + b = 6 ...(ii)

Multiplying (ii) by 4

16a + 4b = 24

9a + 4b = 10

Subtracting, 16a + 4b = 24

7a = 14

7a = 14

⇒ a = 14/7 = 2

Subtracting the value of a in (i)

9(2) + 4b = 10

⇒ 18 + 4b = 10

⇒ 4b = 10 - 18

⇒ 4b = - 8

∴ b = - 8/4 = - 2



Hence a = 2, b = - 2

∴ f(x) = ax³ + 3x² + bx - 3

= 2x³ + 3x² - 2x - 3

∵ 2x + 3 is a factor

∴ Dividing f(x) by x + 2


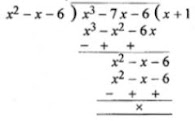
∴ 2x³ + 3x² - 2x - 3

= (2x + 3)(x² - 1) = (2x + 3)[(x)² - (1)²]

= (2x + 3)(x + 1)(x - 1)





27. If ax³ + 3x² + bx - 3 has a factor (2x + 3) and leaves remainder - 3 when divided by (x + 2), find the values of a and 6. With these values of a and 6, factorise the given expression.



Answer

Let 2x + 3 = 0 then 2x = - 3

⇒ x = (-3)/2

Substituting the value of x in f(x),

f(x) = ax³ + 3x² + 6x - 3

f(-3/2) = a(-3/3)3 + 3(-3/2)2 + b(-3/2) - 3

= a(- 27/8) + 3(9/4) + b(-3/2) - 3

= - 27a/8 + 27/4 - 3b/2 - 3

∵ 2x + 3 is a factor of f(x)
∴ Remainder = 0





28. Given f(x) = ax² + bx + 2 and g(x) = bx² + ax + 1. If x - 2 is a factor of f(x) but leaves the remainder - 15 when it divides g(x), find the values of a and b. With these values of a and b, factorise the expression. f(x) + g(x) + 4x² + 7x.



Answer

f(x) = ax² + bx + 2

g(x) = bx² + ax + 1

x - 2 is a factor of f(x)

Let x - 2 = 0

⇒ x = 2

∴ f(2) = a(2)² + b × 2 + 2

= 4a + 2b + 2

∴ 4a + 2b + 2 = 0 (∵ x - 2 is its factor)

⇒ 2a + b + 1 = 0 ....(i) (Dividing by 2)

Dividing g(x) by x - 2, remainder = - 15

Let x - 2 = 0

⇒ x = 2

∴ g(2) = b(2)² + a × 2 + 1

= 4b + 2a + 1

∵ Remainder is - 15

∴ 4b + 2a + 1 = - 15

⇒ 4b + 2a + 1 + 15 = 0

⇒ 4b + 2a + 16 = 0

⇒ 2b + a + 8 = 0 (Dividing by 2)

⇒ a + 2b + 8 = 0 ...(ii)

Multiplying (i) by 2 and (ii) by 1

4a + 2b + 2 = 0

a + 2b + 8 = 0

3a - 6 = 0

⇒ 3a = 6

⇒ a = 6/3

∴ a = 2

Substituting the value of a in (i)

2 × 2 + b + 1 = 0

⇒ 4 + b + 1 = 0

⇒ b + 5 = 0

⇒ b = - 5

Hence a = 2, b = - 5

Now f(x) + g(x) = 4x² + 7x

= 2x² - 5x + 2 + (-5x² + 2x + 1) + 4x² + 7x

= 2x² - 5x + 2 - 5x² + 2x + 1 + 4x² + 7x

= 6x² - 5x² - 5x + 2x + 7x + 2 + 1

= x²+ 2x + 3

= x² + x + 3x + 3

= x(x + 1) + 3(x + 1)
= (x + 1)(x + 3)





Multiple Choice Questions

Choose the correct answer from the given four options (1to 5):


1. When x³ - 3x² + 5x - 7 is divided by x - 2, then the remainder is. .



(a) 0



(b) 1



(c) 2



(d) - 1



Answer


(d) - 1

f(x) = x³ - 3x² + 5x - 7

g(x) = x - 2, if x - 2 = 0, then x = 2

Remainder will be

∴ f(2) = (2)² - 3(2)² + 5 × 2 - 7

= 8 - 12 + 10 - 7

= 18 - 19

= - 1

∴ Remainder = - 1





2. When 2x³ - x² - 3x + 5 is divided by 2x + 1, then the remainder is



(a) 6



(b) - 6



(c) - 3



(d) 0



Answer


(a) 6

f(x) = 2x³ - x² - 3x + 5

g(x) = 2x + 1

Let 2x + 1 = 0, then x = -1/2

Then remainder will be

f(-1/2) = 2(-1/2)³ - (-1/2)² - 3(-1/2) + 5

= 2 × -1/8 - 1/4 + 3/2 + 5

= -1/4 - 1/4 + 3/2 + 5

= (- 1 - 1 + 6 + 20)/4

= 24/4

= 6

∴ Remainder = 6





3. If on dividing 4x² - 3kx + 5 by x + 2, the remainder is - 3 then the value of k is



(a) 4



(b) - 4



(c) 3



(d) - 3



Answer


(b) - 4

f(x) = 4x² - 3kx + 5

g(x) = x + 2

Remainder = - 3

Let x + 2 = 0, then x = - 2

Now remainder will be

f(-2) = 4(-2)² - 3k(-2) + 5

= 16 + 6k + 5

= 21 + 6k

∴ 21 + 6k = - 3

⇒ k = - 24/6

= - 4

∴ k = - 4





4. If on dividing 2x³ + 6x²
- (2k - 7)x + 5 by x + 3, the remainder is k - 1 then the value of k is



(a) 2



(b) - 2



(c) - 3



(d) 3



Answer


(d) 3

f(x) = 2x³ + 6x² - (2k - 7)x + 5

g(x) = x + 3

Remainder = k - 1

If x + 3 = 0, then x = - 3

∴ Remainder will be

f(-3) = 2(-2)³ + 6(-3)² - (2k - 7) (-3) + 5

= -54 + 54 + 3(2k - 7) + 5

= -54 + 54 + 6k - 21 + 5

= 6k - 16

∴ 6k - 16 = k - 1

6k - k = - 1 + 16

⇒ 5k = 15

⇒ k = 15/5 = 3
∴ k = 3





5. If x + 1 is a factor of 3x³ + kx² + 7x + 4, then the value of k is



(a) - 1



(b) 0



(c) 6



(d) 10



Answer


(c) 6

f(x) = 3x³ + kx² + 7x + 4

g(x) = x + 1

Remainder = 0

Let x + 1 = 0, then x = - 1

f(-1) = 3(-1)³ + k(-1)² + 7(-1) + 4

= - 3 + k - 7 + 4

= k - 6

∴ Remainder = 0

∴ k - 6 = 0

⇒ k = 6





Chapter Test

1. Find the remainder when 2x³ - 3x² + 4x + 7 is divided by


(i) x - 2


(ii) x + 3


(iii) 2x + 1



Answer

f(x) = 2x³ - 3x² + 4x + 7

(i) Let x - 2 = 0, then x = 2

Substituting value of x in f(x)

f(2) = 2(2)³ - 3(2)² + 4(2) + 7

= 2 × 8 - 3 × 4 + 4 × 2 + 7

= 16 - 12 + 8 + 7

= 19

Remainder = 19

(ii) Let x + 3 = 0, then x = - 3

Substituting the value of x in f(x)

f(-3) = 2(-3)³ - 3(-3)² + 4(-3) + 7

= 2 ×(-27) - 3(9) + 4(-3) + 7

= - 54 - 27 - 12 + 7

= - 93 + 7

= - 86

∴ Remainder = - 86

(ii) Let 2x + 1 = 0, then 2x = - 1

⇒ x = - (1/2)

Now substituting the value of x in f(x)

f(- 1/2) = 2(- 1/2)³ - 3(- 1/2)² + 4(- 1/2) + 7

= 2 ( - 1/8) - 3(1/4) + 4(- 1/2) + 7

= - 1/4 - 3/4 - 2 + 7

= - 1 - 2 + 7

= 4
∴ Remainder = 4





2. When 2x³ - 9x² + 10x - p is divided by (x + 1), the remainder is - 24. Find the value of p.



Answer

Let x + 1 = 0 then x = - 1

Substituting the value of x in f(x)

f(x) = 2x³ - 9x² + 10x - p

f(-1) = 2(-1)³ - 9(-1)² + 10(-1) - p

= - 2 - 9 - 10 - p

= - 21 - p

∵ - 21 - p = - 24

⇒ - p = - 24 + 21 = - 3

∴ p = 3





3. If (2x - 3) is a factor of 6x² + x + a, find the value of a. With this value of a, factorise the given expression.



Answer

Let 2x - 3 = 0 then 2x = 3

⇒ x = 3/2

Substituting the value of x in f(x)

f(x) = 6x² + x + a

f(3/2) = 6(3/2)² + 3/2 + a

= 6 × 9/4 + 3/2 + a

= 27/2 + 3/2 + a

= 30/2 + a

= 15 + a

∴ 2x - 3 is the factor

∴ Remainder = 0

∴ 15 + a = 0

⇒ a = - 15

Now f(x) will be 6x² + x - 15 s

Dividing 6x² + x - 15 by 2x - 3, we get

∴ 6x² + x - 15 = (2x - 3)(3x + 5)





4. When 3x² - 5x + p is divided by (x - 2), the remainder is 3. Find the value of p. Also the polynomial 3x² - 5x + p - 3.



Answer

f(x) = 3x² - 5x + p

Let (x - 2) = 0, then x = 2

f(2) = 3(2)² - 5(2) + p

= 3 × 4 - 10 + p,

= 12 - 10 + p

= 2 + p

∵ Remainder = 3

∴ 2 + p = 3

⇒ p = 3 - 2 = 1

Hence p = 1

Now f(x) = 3x² - 5x + p - 3

= 3x² - 5x + 1 - 3

= 3x² - 5x - 2

Dividing by (x - 2), we get

3x² - 5x - 2 = (x - 2)(3x + 1)





5. Prove that (5x + 4) is a factor of 5x³ + 4x² - 5x - 4. Hence factorize the given polynomial completely.



Answer

f(x) = 5x³ + 4x² - 5x - 4

Let 5x + 4 = 0, then 5x = - 4

⇒ x = - 4/2

∴ f( - 4/5) = 5(- 4/5)³ + 4(- 4/5)2 - 5( - 4/5) - 4

= 5 × ( - 64/125) + 4 × 16/25 + 4 - 4

= - 64/25 + 64/25 + 4 - 4

= 0

∵ f(-4/5) = 0

∴ (5x + 4) is a factor of f(x)

Now, dividing f(x) by 5x + 4, we get

5x³ + 4x² - 5x - 4

= (5x + 4)(x² - 1)

= (5x + 4){(x)² - (1)²}
= (5x + 4)(x + 1)(x - 1)




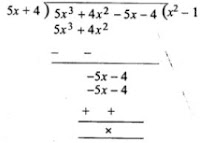
6. Use factor theorem to factorise the following polynomials completely:


(i) 4x³ + 4x² - 9x - 9


(ii)
x³
- 19x - 30



Answer

(i) f(x) = 4x³ + 4x² - 9x - 9

Let x = - 1, then

f(-1) = 4(1)³ + 4(-1)² - 9(1) - 9

= - 4 + 4 + 9 - 9

= 13 - 13

= 0

∴ (x + 1) is a factor of f(x)

Now dividing f(x) by x + 1, we get

f(x) = 4x³ + 4x² - 9x - 9

= (x + 1)(4x² - 9)

= (x + 1){(2x)² - (3)²}

= (x + 1)(2x + 3)(2x - 3)


(ii) f(x) = x³ - 19x - 30

Let x = - 2, then

f(-2) = (-2)² - 19(-2) - 30

= - 8 + 38 - 30

= - 38 - 38

= 0

∴ (x + 2) is a factor of f(x).

Now dividing f(x) by (x + 2), we get

f(x) = x³ - 19x - 30

= (x + 2) (x² - 2x - 15)

= (x + 2){(x² - 5x + 3x - 15)}

= (x + 2){x(x - 5) + 3(x - 5)}

= (x + 2)(x - 5)(x + 3)





7. If x³ - 2x² + px + q has a factor (x + 2) and leaves a remainder 9, when divided by (x + 1), find the values of p and q. With these values of p and q, find the values of p and q. With these values of p and q, factorize the given polynomial completely.



Answer

f(x) = x³ - 2x² + px + q

(x + 2) is a factor

f(-2) = (-2)³ - 2(-2)² + p(-2) + q

= - 8 - 2 × 4 - 2p + q

= - 8 - 8 - 2p + q

= - 16 - 2p + q

∵ (x + 2) is a factor of f(x)

∴ f(-2) = 0

⇒ - 16 - 2p + q = 0

⇒ 2p - q = - 16 ...(i)

Again, let x + 1 = 0, then x = - 1

∴ f(-1) = (- 1)³ - 2(-1)² + p(-1) + q

= - 1 - 2 × 1 - p + q

= - 1 - 2 - p + q

= - 3 - p + q

∵ Remainder = 9, then

- 3 - p + q = 9

⇒ - p + q = 9 + 3 = 12

- p + q = 12 ...(ii)

Adding (i) and (ii)

p = - 4

Substituting the value of p in (ii)

- (- 4) + q = 12

4 + q = 12

⇒ q = 12 - 4 = 8

∴ p = - 4, q = 8

∴ f(x) = x³ - 2x² - 4x + 8

Dividing f(x) by (x + 2), we get

f(x) = (x + 2)(x² - 4x + 4)

= (x + 2){(x)² - 2 × x(-2) + (2)²}
= (x + 2)(x - 2)²





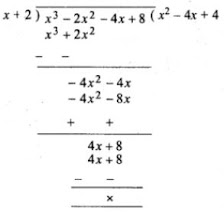
8. If (x + 3) and (x - 4) are factors of x³ + ax² - bx + 24, find the values of a and b: with these values of a and b, factorise the given expression.



Answer

f(x) = x³ + ax² - bx + 24

Let x + 3 = 0, then x = - 3

Substituting the value of x in f(x)

f(-3) = (-3)³ + a(- 3)² - b(-3) + 24,

= - 27 + 9a + 3b + 24

= 9a + 3b - 3

∵ Remainder = 0,

∴ 9a + 3b - 3 = 0

⇒ 3a + b - 1 = 0 (Dividing by 3)

⇒ 3a + b = 1 ...(i)

Again Let x - 4 = 0, then x = 4

Substituting the value of x in f(x)

f(x) = (4)³ + a(4)² - b(4) + 24

= 64 + 16a- 4b + 24

= 16a - 4b + 88

∵ x - 4 is a factor

∴ Remainder = 0

16a - 4b + 88 = 0

⇒ 16a - 4b = - 88 (Dividing by 4)

⇒ 4a - b = - 22

Adding (i) and (ii),

7a = - 21,

⇒ a = - 3

Substituting the value of a in (i)

3(-3) + b = 1

⇒ - 9 + b = 1

⇒ b = 1 + 9 = 10

Now f(x) will be

f(x) = x³ - 3x² - 10x + 24

∵ x + 3 and x - 4 are factors of f(x)

∴ Dividing f(x) by (x + 3)(x - 4)

or x² - x - 12


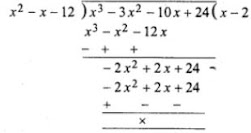
x³ - 3x² - 10x + 24

= (x² - x - 12)(x - 2)

= (x + 3)(x - 4)(x - 2)





9. If 2x³ + ax² - 11x + b leaves remainder 0 and 42 when divided by (x - 2) and (x - 3) respectively, find the values of a and b. With these values of a and b, factorize the given expression.



Answer

f(x) = 2x³ + ax² - 11x + b

Let x - 2 = 0, then x = 2,

Substituting the value of x in f(x)

f(2) = 2(2)³ + a(2)² - 11(2) + b

= 2 × 8 + 4a - 22 + b

= 16 + 4a - 22 + b

= 4a + b - 6

∵ Remainder = 0,

∴ 4a + b - 6 = 0

⇒ 4a + b = 6 ...(i)

Again let x - 3 = 0, then x = 3

Substituting the value of x is f(x)

f(3) = 2(3)³ + a(3)² - 11 × 3 + b

= 2 × 27 + 9a - 33 + b

= 54 + 9a - 33 + b

⇒ 9a + b + 21

∵ Remainder = 42

∴ 9a + b + 21 = 42

⇒ 9a + b = 42 - 21

⇒ 9a + b = 21 ....(ii)

Subtracting (i) from (ii)

5a = 15

⇒ a = 15/5 = 3

Substituting the value of a is (i) 4(3) + b = 6

⇒ 12 + b = 6

⇒ b = 6 - 12

⇒ b = - 6

∴ f(x) will be 2x³ + 3x² - 11x - 6

∵ x - 2 is a factor (as remainder = 0)

∴ Dividing f(x) by x - 2, we get


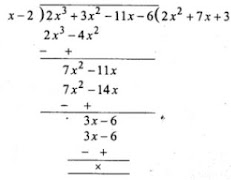
∴ 2x³ + 3x² - 11x - 6

= (x - 2)(2x² + 7x + 3)

= (x - 2)[2x² + 6x + x + 3]

= (x - 2)[2x(x + 3) + 1(x + 3)]
= (x - 2)(x + 3)(2x + 1)





10. If (2x + 1) is a factor of both the expressions 2x² - 5x + p and 2x² + 5x + q, find the value of p and q. Hence find the other factors of both the polynomials.



Answer

Let 2x + 1 = 0, then 2x = - 1

x = - (1/2)

Substituting the value of x in

f(x) = 2x² - 5x + p

f(-1 /2) = 2(-1/2)² - 5(-1/2) + p

= 2 × 1/4 + 5/2 + p

= 1/2 + 5/2 + p

= 3 + p

∵ 2x + 1 is the factor of p(x)

∴ Remainder = 0

⇒ 3 + p = 0

⇒ p = - 3

Again substituting the value of x in q(x)

q(x) = 2x² + 5x + q

q(- 1/2) = 2(- 1/2)² + 5(- 1/2) + q

= 2 × 1/4 - 5/2 + q

= 1/2 - 5/2 + q

= - 4/2 + q

= q - 2

∵ 2x + 1 is the factor of q(x)

∴ Remainder = 0

⇒ q - 2 = 0

⇒ q = 2

Hence p = - 3, q = 2

Now (i) ∵ 2x + 1 is the factor of p(x)

= 2x² - 5x - 3

∴ Dividing p(x) by 2x + 1,


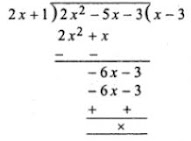
∴ 2x² - 5x - 3 = (2x + 1)(x - 3)

(ii) ∵ 2x + 1 is the factor of q(x) = 2x² + 5x + 2

∴ Dividing q(x) by 2x + 1,


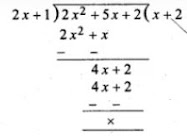
∴ 2x² + 5x + 2 = (2x + 1)(x + 2)





11. If a polynomial f(x) = x⁴ - 2x³ - 3x² - ax - b leaves remainder 5 and 19 when divided by (x - 1) and (x + 1) respectively, Find the values of a and b. Hence determined the remainder when f(x) is divided by (x - 2).



Answer

f(x) = x⁴ - 2x³ + 3x² - ax + b

f(1) = 5 and f(-1) = 19

∴ (1)⁴ - 2(1)³ + 3(1)² - a (1) + b = 5

And (-1)⁴ - 2(-1)³ + 3(-1)² - a(-1) + b = 19

⇒ 1 - 2 + 3 - a + b = 5

and 1 + 2 + 3 + a + b = 19

⇒ - a + b = 5 - 2 and a + b = 19 - 6

⇒ a+ b = 3 ....(i)

and a + b = 13 ....(ii)

On subtracting (i) and (2), we het

a + b - (- a + b) = 13 - 3

a + b + a - b = 10

2a = 10

a = 5

putting a = 5 in equation 1, we get

= 5 + b = 3, b = 8
a = 5, b = 8





12. When a polynomial f(x) is divided by (x - 1), the remainder I 5 and when it is, divided by (x - 2), the remainder is 7. Find - the remainder when it is divided by (x - 1)(x - 2).



Answer

When f(x) id divided by (x - 1),

Remainder = 5

Let x - 1 = 0

⇒ x = 1

∴ f(1) = 5

When divided by (x - 2), Remainder = 7

Let x - 2 = 0

⇒ x = 2

∴ f(2) = 7

Let f(x) = (x - 1)(x - 2)q(x) + ax + b

Where q(x) is the quotient and ax + b is remainder

Putting x = 1, we get:

f(1) = (1 - 1) (1 - 2) q(1) + a × 1 + b

= 0 + a + b

= a + b

And x = 2, then

f(2) = (2 - 1)(2 - 2) q(2) + a ×1 + b

= 0 + 2a + b

= 2a + b

∴ a + b = 5 ...(i)

2a + b = 7 ....(ii)

Subtracting, we get

- a = - 2

⇒ a = 2

Substituting the value of a in (i)

2 + b = 5

⇒ b = 5 - 2 = 3

∴ a = 2, b = 3

∴ Remainder = ax + b
= 2x + 3

•