ICSE-X-Mathematics
04: Linear Inequations Class 10 Maths ML Aggarwal Solutions
1. Solve the inequation 3x - 11 < 3 where x
∈
{1, 2, 3, ........, 10}. Also represent its solution on a number line
Answer
3x - 1 < 3
⇒ 3x < 3 + 11
⇒ 3x < 14x < 14/3
But x ∈ 6 {1, 2, 3, 4}.
Solution set on number line
2. Solve 2(x - 3) < 1, x
∈
{1, 2, 3, ..... 10}
Answer
2(x - 3) < 1
⇒ x - 3 < 1/2
⇒ x < 1/2 + 3
⇒ x < 3.1/2
But x ∈ {1, 2, 3..... 10}
Solution set = {1, 2, 3}

3. Solve: 5 - 4x > 2 - 3x, x
∈
W. Also represent its solution on the number line.
Answer
5 - 4x > 2 - 3x
⇒ -4x + 3x > 2 - 5
⇒ - x > - 3
x ∈ w,
Solution set {0, 1, 2}
Solution set on number line:

4. List the solution set of 30 - 4(2x - 1) < 30, given that x is a positive integer.
Answer
30 - 4 (2x - 1) < 30
⇒ 30 - 8x + 4 < 30
⇒ - 8x < 30 - 30 - 4
⇒ - 8x < - 4x > -4/-8
⇒ x > 1/2
x is a positive integer
x = {1, 2, 3, 4, .... }
5. Solve : 2(x - 2) < 3x - 2, x
∈
{-3, -2, - 1, 0, 1, 2, 3}
Answer
2(x - 2) < 3x - 2
⇒ 2x - 4 < 3x - 2
⇒ 2x - 3x < - 2 + 4
⇒ - x < 2
⇒ x > - 2
Solution set = {- 1, 0, 1, 2, 3}
6. If x is a negative integer, find the solution set of 2/3 + 1/3 (x + 1) > 0.
Answer
2/3 + 1/3x + 1/3 > 0
⇒ 1/3x + 1 > 0
⇒ 1/3x > - 1
⇒ x > - 1 × 3/1 ⇒ x > - 3
7. Solve: (2x - 3)/4 ≥ 1/2, x
∈
{0, 1, 2, ....., 8}
Answer 7
(2x - 3)/4 ≥ 1/2
⇒ 2x - 3 ≥ 2 ⇒ 2x ≥ 2 + 3
⇒ 2x ≥ 5 ⇒ x ≥ 5/2
∵ x ∈ {0, 1, 2, ......., 8}
∴ Solution set = {3, 4, 5, 6, 7, 8}
8. Solve x - 3(2 + x) > 2 (3x - 1), x
∈
{-3, -2, -1, 0, 1, 2, 3}. Also represent its solution on the number line.
Answer
x - 3 (2 + x) > 2(3x - 1)
⇒ x - 6 - 3x > 6x - 2
⇒ x - 3x - 6x > - 2 + 6
⇒ - 8x > 4
⇒ x < -4/8 ⇒ x < - 1/2
x ∈ {-3, -2, -1, 0, 1, 2}
∴ Solution set = {-3, -2, -1}
Solution set on Number line:

9. Given x
∈
{1, 2, 3, 4, 5, 6, 7, 9} solve x - 3 < 2x - 1.
Answer
x - 3 < 2x - 1
⇒ x - 2x < - 1 + 3
⇒ - x < 2x > - 2
But x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4, 5, 6, 7, 9}
10. Given A = {x : x
∈
I, - 4 ≤ x ≤ 4}, solve 2x - 3 < 3 where x has the domain A Graph the solution set on the number line.
Answer
2x - 3 < 3
⇒ 2x < 3 + 3
⇒ 2x < 6
⇒ x < 3
But x has the domain A = {x : x ∈ I - 4 ≤ x ≤ 4}
Solution set = {-4, - 3, -2, -1, 0, 1, 2}
Solution set on number line:

11. List the solution set of the inequation 1/2 + 8x > 5x - 3/2, x
∈
Z
Answer :
1/2 + 8x > 5x - 3/2
⇒ 8x - 5x > - 3/2 - 1/2
⇒ 3x > - 2 ⇒ x > - 2/3
∵ x ∈ Z,
∴ Solution set = {0, 1, 2, 3, 4 ,.......}
12. List the solution set of (11 - 2x)/5 ≥ (9 - 3x)/8 + 3/4, x
∈
N
Answer :
(11 - 2x)/5 ≥ (9 - 3x)/8 + 3/4
⇒ 88 - 16x ≥ 45 - 15x + 30
(L.C.M. of 8, 5, 4 = 40}
⇒ - 16x + 15x ≥ 45 + 30 - 88
⇒ - x ≥ - 13
⇒ x ≤ 13
x ≤ N
Solution set = {1, 2, 3, 4, 5, ....., 13}
13. Find the values of x, which satisfy the inequation : - 2 ≤ 1/2 - 2x/3 ≤ 1.5/6, x
∈
N.
Graph the solution set on the number line.
Answer
- 2 ≤ 1/2 - 2x/3 ≤ 1.5/6, x ∈ N
⇒ - 2 - 1/2 ≤ 1/2 - 2x/3 - 1/2 ≤ 11/6 - 1/2
[By subtracting 1/2 on both sides of inequality]
⇒ - 5/2 ≤ 2x/3 ≤ 8/6
⇒ - 15 ≤ - 4x ≤ 8
⇒ 15 ≥ 4x ≥ - 8
⇒ 15/4 ≥ x ≥ - 2
3.3/4 ≥ x ≥ - 2
But x ∈ N, hence only possible solution for x = {1, 2, 3}

14. If x
∈
W, find the solution set of 3/5x - (2x - 1)/3 > 1
Also graph the solution set on the number line, if possible.
Answer
3/5x - (2x - 1)/3 > 1
⇒ 9x - (10x - 5) > 15 (L.C.M. of 5, 3 = 15)
⇒ 9x - 10x + 5 > 15
⇒ - x > 15 - 5
⇒ - x > 10
⇒ x < - 10
But x ∈ W
Solution set = Φ
Hence it can’t be represented on number line.
15. Solve:
(i) x/2 + 5 ≤ x/3 + 6 where x is a positive odd integer.
(ii) (2x + 3)/3 ≥ (3x - 1)/4 where x is positive even integer.
Answer
(i) x/2 + 5 ≤ x/3 + 6
⇒ x/2 - x/3, ≤ 6 - 5
⇒ (3x - 2x)/6 ≤ 1
⇒ x/6 ≤ 1
⇒ x ≤ 6
∵ x is a positive odd integer
∴ x = {1, 3, 5}
(ii) (2x + 3)/3 ≥ (3x - 1)/4
⇒ 2x/3 + 3/3 ≥ 3x/4 - 1/4
⇒ 2x/3 - 3x/4 ≥ -1/4 - 1
⇒ (8x - 9x)/12 ≥ - 5/4
⇒ -x/12 ≥ -5/4
⇒ x/12 ≤ 5/4
⇒ x ≤ 5/4 × 12
⇒ x ≤ 15
∵ x is positive even integer
∴ x = {2, 4, 6, 8, 10, 12, 14}
16. Given that x ∈ I, solve the inequation and graph the solution on the number line:
3 ≥ (x - 4)/2 + x/3 and 3 ≥ (x - 4)/2 + x/3 ≥ 2
Answer
(i) 3 ≥ (3x - 12 + 2x)/6
⇒ 3 ≥ (5x - 12)/6
⇒ 18 ≥ 5x - 12
⇒ 5x - 12 ≤ 18
⇒ 5x ≤ 18 + 12
⇒ 5x ≤ 30
⇒ x ≤ 6
(ii) (x - 4)/2 + x/2 ≥ 2
(3x - 12 + 2x)/6 ≥ 2
⇒ (5x - 12)/6 ≥ 2
⇒ 5x - 12 ≥ 12
⇒ 5x ≥ 12 + 12, x ≥ 24/5
⇒ x ≥ 4.4/5
∴ x = {5, 6}
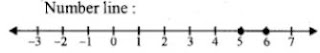
17. Given x
∈
{1, 2, 3, 4, 5, 6, 7, 9}, find the values of x for which - 3 < 2x - 1 < x + 4.
Answer
- 3 < 2x - 1 < x + 4
⇒ - 3< 2x - 1 and 2x - 1 < x + 4
⇒ - 2x < - 1 + 3 and 2x - x < 4 + 1
⇒ -2x < 2 and x < 5
⇒ - x < 1
⇒ x > - 1
- 1 < x < 5
x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4}
18. Solve: 1 ≥ 15 - 7x > 2x - 27, x
∈
N
Answer
1 ≥ 15 - 7x > 2x - 27
1 ≥ 15 - 7x and 15 - 7x > 2x - 27
⇒ 7x ≥ 15 - 1 and - 7x - 2x > - 27 - 15
⇒ 7x ≥ 14 and - 9x > - 42
⇒ x ≥2 and - x > - 42/9
⇒ 2 ≤ x and - x > - 14/3 and x < 14/3
2 ≤ x < 14/3
But x ∈ N
∴ Solution set = {2, 3, 4}
19. If x
∈
Z, solve 2 + 4x < 2x - 5 ≤ 3x. Also represent its solution on the number line.
Answer
2 + 4x < 2x - 5 ≤ 3x
2 + 4x < 2x - 5 and 2x - 5 ≤ 3x
⇒ 4x - 2x < -5 - 2, and 2x - 3x ≤ 5
⇒ 2x < - 7 and - x ≤ 5
⇒ x < - (7/2) and x ≥ - 5 and - 5 ≤ x
∴ - 5 ≤ x < -(7/2)
∵ x ∈ Z
∴ Solution set = {- 5, -4}
Solution set on Number line
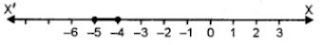
20. Solve the inequation = 12 + 1.5/6x ≤ 5 + 3x , x
∈
R. Represent the solution on a number line.
Answer
12 + 11/6.x ≤ 5 + 3x
⇒ 72 + 11x ≤ 30 + 18x (Multiplying by 6)
⇒ 11x - 18x ≤ 30 - 72
⇒ - 7x ≤ - 42
⇒ - x ≤ -(42/7)
⇒ - x ≤ - 6
⇒ x ≥ 6
∴ x ∈ R
∴ Solution set = {x : x ∈ R, x ≥ 6}
Solution set on Number line

21. Solve: (4x - 10)/3 ≤ (5x - 7)/2 x
∈
R and represent the solution set on the number line.
Answer
(4x - 10)/3 ≤ (5x - 7)/2
⇒ 8x - 20 ≤ 15x - 21
(L.C.M. of 3, 2 = 6)
⇒ 8x - 15x ≤ - 21 + 20
⇒ - 7x ≤ - 1 ⇒ - x ≤ - (1/7)
⇒ x > 1/7
∵ x ∈ R
∴ Solution set = {x : x ∈ R, x > 1/7}
Solution set on the number line

22. Solve 3x/5 - (2x - 1)/3 > 1, x
∈
R and represent the solution set on the number line.
Answer
3x/5 - (2x - 1)/3 > 1
⇒ 9x - (10x - 5) > 15
⇒ 9x - 10x + 5 > 15
⇒ - x > 15 - 5
⇒ - x > 10
⇒ x < - 10
x ∈ R.
∴ Solution set = {x : x ∈ R, x < - 10}
Solution set on the number line
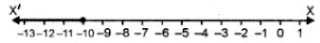
23. Solve the inequation - 3 ≤ 3 - 2x < 9, x
∈
R. Represent your solution on a number line.
Answer
- 3 ≤ 3 - 2x < 9
⇒ - 3 ≤ 3 - 2x and 3 - 2x < 9
⇒ 2x ≤ 3 + 3 and - 2x < 9 - 3
⇒ 2x ≤ 6 and - 2x - 6
⇒ x ≤ 3 and - x < 3
⇒ x ≤ - 3 and - 3 < x
- 3 < x ≤ 3.
Solution set = {x : x ∈ R, - 3 < x ≤ 3)
Solution on number line

24. Solve 2 ≤ 2x - 3 ≤ 5, x R and mark it on number line.
Answer
2 ≤ 2x - 3 ≤ 5 or 2 ≤ 2x - 3 and 2x - 3 ≤ 5 or 2 + 3 ≤ 2x and 2x ≤ 5 + 3
5 ≤ 2x and 2x ≤ 8
5/2 ≤ 2x and 2x ≤ 8
5/2 ≤ x and x ≤ 4
∴ 5/2 ≤ x and x ≤ 4
∴ Solution set = {x : x ∈ R, 5/2 ≤ x ≤ 4}
Solution set on number line

25. Given that x
∈
R, solve the following inequation and graph the solution on the number line: - 1 ≤ 3 + 4x < 23.
Answer
We have
- 1 ≤ 3 + 4x < 23
⇒ - 1 - 3 ≤ 4x < 23 - 3
⇒ - 4 ≤ 4x < 20
⇒ - 1 ≤ x < 5, x ∈ R
Solution Set = { - 1 ≤ x < 5; x ∈ R}
The graph of the solution set is shown below:
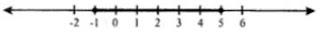
26. Solve the following inequation and graph the solution on the number line.
- 2.2/3 ≤ x + 1/3 < 3 + 1/3 x
∈
R
Answer
Given - 2. 2/3 ≤ x + 1/3 + 1/3 x ∈ R
- 8/3 ≤ x + 1/3 < 10/3
Multiplying by 3, L.C.M. of fractions, we get
- 8 ≤ 3x + 1 < 10
- 8 - 1 ≤ 3x + 1 - 1 < 10 - 1 [Add - 1]
- 9 ≤ 3x < 9
- 3 ≤ x < 3 [Dividing by 3]
Hence, the solution set is {x : x ∈ R, - 3 ≤ x < 3}
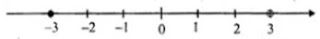
The graph of the solution set is shown by the thick portion of the number line. The solid circle at - 3 indicates that the number - 3 is indicates that the number - 3 is included among the solutions whereas the open circle at 3 indicates that 3 is not included among the solutions.
27. Solve the following inequation and represent the solution set on the number line:
- 3 < - (1/2) - 2x/3 ≤ 5.6, x
∈
R
Answer
- 3 < - (1/2) - 2x/3 ≤ 5/6, x ∈ R
(i) - 3 < - 1/2 - 2x/3 ⇒ - 3 < (1/2 + 2x/3
⇒ - (1/2 + 2x/3) > - 3
⇒ - 2x/3 > - 3 + 1/2
⇒ - 2x/3 > -5/2
⇒ 2x/3 < 5/2
⇒ x < 5/2 × 3/2
⇒ x < 15/4 ...(i)
(ii) - (1/2) - 2x/3 ≤ 5/6
⇒ - (2x/3) ≤ 5/6 + 1/2
⇒ -2x/3 ≤ (5 + 3)/6
⇒ -2/3.x ≤ 8/6
⇒ 2/3.x ≥ -8/6
⇒ x ≥ - 8/6 ×3/2
⇒ x ≥ - 2
⇒ - 2 ≤ x ...(ii)
From (i) and (ii),
- 2 ≤ x ≤ 15/4
∴ Solution = {x : x ∈ R, - 2
≤ x < 15/4}
Now solution on number line
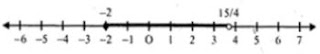
28. Solve (2x + 1)/2 + 2(3 - x) ≤ 7, x
∈
R. Also graph the solution set on the number line.
Answer
(2x + 1)/2 + 2(3 - x) ≥ 7, x ∈ R
⇒ (2x + 1)/2 + 6 - 2x ≥ 7
⇒ (2x + 1)/2 - 2x ≥ 7 - 6
⇒ (2x + 1 - 4x)/2 ≥ 1
⇒ 2x + 1 - 4x ≥ 2
⇒ - 2x ≥ 2 - 1
⇒ - 2x ≥ 1
⇒ - x ≥ 1/2
⇒ x ≤ - 1/2
∴ Solution set {x: x ∈ R, x ≤ - 1/2}
Solution on number line:

29. Solving the following inequation, write the solution set and represent it on the number line. - 3(x - 7) ≥ 15 - 7x > (x + 1)/3, n
∈
R
Solution:
- 3(x - 7) ≥ 15 - 7x > (x + 1)/3, n ∈ R
⇒ -3(x - 7) ≥ 15 - 7x ⇒ - 3x + 21 ≥ 15 - 7x
⇒ - 3x + 7x ≥ 15 - 21 ⇒ 4x ≥ - 6
⇒ x ≥ -6/4
⇒ x ≥ -3/2
⇒ -3/2 ≤ x
And 15 - 7x > (x + 1)/3
⇒ 45 - 21x > x + 1
⇒ 45 - 1 > x + 21x
⇒ 44 > 22x
2 > x ⇒ x = 2
∴ -3/2 ≤ x < 2, x ∈ R

30. Solving the following inequation, write the solution set and represent it on the real number line.
- 2 + 10x ≤ 13x + 10 < 24 + 10x, x
∈
Z.
Answer
Given, - 2 + 10x ≤ 13x + 10 < 24 + 10x, x ∉ Z
⇒ - 2 - 10 ≤ 13x - 10x
⇒ - 12 ≤ 3x
⇒ - 4 ≤ x
Also 13x + 10 < 24 + 10x
⇒ 13x - 10x < 24 - 10
3x < 14
∴ x < 4.2/3
∴ - 4 ≤ x < 4.2/3
dlt22274371707752935229">
31. Solve the inequation 2x - 5 ≤ 5x + 4 < 11, where x
∈
I. Also represent the solution set on the number line.
Answer
2x - 5 ≤ 5x + 4 < 11
⇒ 2x - 5 ≤ 5x + 4
⇒ 2x - 5 - 4 ≤ 5x and 5x + 4 < 11
⇒ 2x - 9 ≤ 5x and 5x < 11 - 4 and 5x < 7
⇒ 2x - 5x ≤ 9 and x < 7/5
⇒ 3x > - 9 and x < 1.4
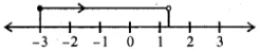
⇒ x > - 3
32. If x
∈
I, A is the solution set of 2(x - 1) < 3 x - 1 and B is the solution set of 4x - 3 ≤ 8 + x, find A
∩ B.
Answer :
2(x - 1)< 3x - 1
⇒ 2x -2 < 3x - 1
⇒ 2x - 3x < - 1 + 2
⇒ - x < 1
⇒ x > - 1
Solution set A = {0, 1, 2, 3,.....,}
4x - 3 ≤ 8 + x
⇒ 4x - x ≤ 8 + 3
⇒ 3x ≤ 11
⇒ x ≤ 11/3
Solution set B = {3, 2, 1, 0, -1, ......}
A ∩ B = {0, 1, 2, 3}
33. If P is the solution set of - 3x + 4 < 2x - 3, x
∈
N and Q is the solution set of 4x
-
5 < 12, x
∈
W, find
(i) P
∩ Q
(ii) Q - P
Answer :
- 3x + 4 < 2x - 3
- 3z - 2z < - 3 - 4
⇒ - 5x < - 7
- x < - 7/5
⇒ x > 7/5
∴ Solution set P = {2, 3, 4, 5, .......}
4x - 5 < 12
4x < 12 + 5 ⇒ 4x < 17
x < 17/4
∵ x ∈ W
∴ Solution set Q = {4, 3, 2, 1, 0}
(i) P ∩ Q = {2, 3, 4}
(ii) Q - P = {1, 0}
34. A = {x : 11x - 5 > 7x + 3, x
∈
R} and B = {x : 18x - 9 ≥ 15 + 12x, x
∈
R}
Find the range of set A ∩
B and represent it on a number line
Answer
A = {x : 11x - 5 > 7x + 3, x ∈ R}
B = {x : 18x - 9 ≥ 15 + 12x, x ∈ R}
Now, A = 11x - 5 > 7x + 3
⇒ 11x - 7x > 3 + 5
⇒ 4x > 8
⇒ x > 2, x ∈ R
B = 18x - 9 ≥ 15 + 12x
⇒ 18x - 12x ≥ 15 + 9
⇒ 6x ≥ 24
⇒ x ≥ 4
∴ A ∩ B = x ≥ 4, x ∈ R
Hence Range of A ∩ B = {x : x ≥ 4, x ∈ R} and its graph will be.
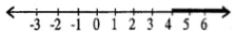
35. Given : P{x : 5 < 2x - 1 ≤ 11, x
∈
R}
Q {x : - 1 ≤ 3 + 4x < 23, x
∈
I) where
R = (real numbers), I = (integers)
Represent P and Q on number line. Write down the elements of P ∩ Q.
Answer
P = {x : 5 < 2x - 1 ≤ 11}
5 < 2x - 1 ≤ 11
⇒ 5 < 2x - 1 and 2x - 1 ≤ 11
⇒ - 2x < - 5 - 1 and 2x ≤ 11 + 1
⇒ - 2x < - 6 and 2x ≤12
⇒ - x < - 3 and x ≤ 6
⇒ x > 3 or 3 < x
∴ Solution set = 3 < x ≤ 6 = {4, 5, 6}
Solution set on number line.

Q = {-1 ≤ 3 + 4x < 23}
- 1 ≤ 3 + 4x < 23
⇒ - 1 < 3 + 4x and 3 + 4x < 23
⇒ - 4x < 3 + 1 4x < 23 - 3
⇒ - 4x < 4 4x < 20
⇒ - x < 1 x < 5
⇒ x > - 1
- 1 < x
∴ - 1 < x < 5
∴ Solution set = {1, 1, 2, 3, 4}
Solution set on number line

36. If x
∈
I, find the smallest value of x which satisfies the inequation 2x + 5/2 > 5x/3 + 2
Answer
2x + 5/2 > 5x/3 + 2
⇒ 2x - 5x/3 > 2 - 5/2
⇒ 12x - 10 x > 12 - 15
⇒ 2x > - 3
⇒ x > - 3/2
Smallest value of x = - 1
37. Given 20 - 5x < 5 (x + 8), find the smallest value of x, when
(i) x
∈
I
(ii) x
∈
W
(iii) x
∈
N
Answer
20 - 5x < 5(x + 8)
⇒ 20 - 5x < 5x + 40
⇒ - 5x - 5x < 40 - 20
⇒ - 10x < 20
⇒ - x < 2
⇒ x > - 2
(i) When x ∈ I, then smallest value = - 1
(ii) When x ∈ W, then smallest value = 0
(iii) When x ∈ N, then smallest value = 1
38. Solve the following inequation and represent the solution set on the number line:
4x - 19 < 3x/5 - 2
≤
- 2/5 + x , x ∈ R
Answer :
We have
4x - 19 < 3x/5 - 2 ≤ - 2/5 + x , x ∈ R
Hence, solution set is {x : - 4 < x < 5, x
The solution set is represented on the number line as below.
⇒ 4x - 19 < 3x/5 - 2 and 3x/5 - 2 ≤ -2/5 + x, x ∈ R
⇒ 4x - 3x/5 < 17 and - 2 + 2/5 ≤ x - 3x/5, x ∈ R
⇒ 17x/5 < 17 and -8/5 ≤ 2x/5, x ∈ R
⇒ x < 5 and - 4 ≤ x, x ∈ R
⇒ - 4 ≤ x < 5, x ∈ R
Hence, solution set is {x : 4 ≤ x < 5, x ∈ R}
The solution set is represented on the number line as below.
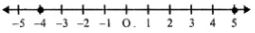
39. Solve the given inequation and graph the solution on the number line:
2y - 3 < y + 1
≤
4y + 7; y ∈ R
Answer
2y - 3 < y + 1 ≤ 4y + 7; y ∈ R
(a) 2y - 3 < y + 1
⇒ 2y - y < 1 + 3
⇒ y < 4
⇒ 4 > y ....(i)
(b) y + 1 ≤ 4y + 7
⇒ y - 4y ≤ 7 - 1
⇒ 3y ≤ 6
⇒ y ≤ 6/-3
⇒ y ≥ - 2 ....(ii)
From (i) and (ii),
4 > y ≥ - 2 or - 2 ≤ y < 4
Now representing it on a number given below
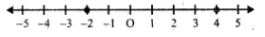
40. Solve the inequation and represent the solution set on the number line.
- 3 + x
≤
8x/3 + 2
≤
14/3 + 2x, where x ∈ I
Answer
Given : - 3 + x ≤ 8x/3 + 2 ≤ 14/3 + 2x, Where x ∈ I
(i) - 3 + x ≤ 8x/3 + 2
⇒ - 3 - 2 ≤ 8x/3 - x
⇒ - 5 ≤ 5x/3
⇒ - 1 ≤ x/3
⇒ - 3 ≤ x ....(i)
And 8x/3 = 2 ≤ 14/3 + 2x
8x/3 - 2x ≤ 14/3 - 2
⇒ 2x/3 ≤ 8/3
⇒ x ≤ 4 ....(ii)
From (i) and (ii)
⇒ - 5 ≤ 5x/3 and 2x/3 ≤ 8/3
⇒ x ≥ - 3 and x ≤ 4
∴ - 3 ≤ x ≤ 4
Solution set = {-3, -2, -1, 0, 1, 2, 3, 4}
Solution set on number line
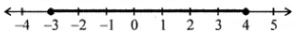
41. Find the greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer.
Answer
Let the greatest integer = x
According to the condition,
2x + 7 > 3x
⇒ 2x - 3x > - 7
⇒ - x > - 7
⇒ x < 7
Value of x which is greatest = 6
42. One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.
Answer
Let the length of the shortest pole = x metre
Length of pole which is buried in mud = x/3
Length of pole which is in the water = x/6
According to this problem,
x - [x/3 + x/6] ≥ 3
⇒ x - (2x + x)/6 ≥ 3
⇒ x - x/2 ≥ 3
⇒ x/2 ≥ 3
⇒ x ≥ 6
∴ Length of pole (shortest in length) = 6 metres
Multiple Choice Questions
1. If x ∈ {- 3, - 1, 0, 1, 3, 5}, then the solution set of the inequation 3x - 2
≤
8 is
(a) { - 3, - 1, 1, 3}
(b) {- 3, - 1, 1, 3}
(c) {- 3, - 2, - 1, 0, 1, 2, 3}
(d) {- 3, - 2, - 1, 0, 1, 2}
Answer
(b) {- 3, - 1, 0, 1, 3}
x ∈ {- 3, - 1, 0, 1, 3, 5}
⇒ 3x - 2 ≤ 8
⇒ 3x ≤ 8 + 2
⇒ 3x ≤ 10
So ⇒ x ≤ 10/3
Therefore ⇒ x < 3.1/3
Solution set = {- 3, - 1, 0, 1, 3}
2. If x ∈ W, then the solution set of the inequation 3x + 11
≥
x + 8 is
(a) {- 2, - 1, 0, 1, 2, ....}
(b) {- 1, 0, 1, 2, ....}
(c) {0, 1, 2, 3, ....}
(d) {x : x ∈ R, x
≥
-(3/2)
Answer
(c) {0, 1, 2, 3,.....}
x ∈ W
3x + 11 ≥ x + 8
⇒ 3x - x ≥ 8 - 11
⇒ 2x ≥ - 3
⇒ x ≥ -3/2
⇒ x ≥ -1.1/2
Solution set = {0, 1, 2, 3,.....}
3. If x ∈ W, the the solution set of the inequation 5 - 4x
≤
2 - 3x is
(a) {....., - 2, - 1, 0, 1, 2, 3}
(b) {1, 2, 3}
(c) {0, 1, 2, 3}
(d) {x : x ∈ R, x
≤
3}
Answer
(c) {0, 1, 2, 3,}
x ∈ W
5 - 4x < 2 - 3x
⇒ 5 - 2 ≤ 3x + 4x
⇒ 3 ≤ x
Solution set = {0, 1, 2, 3,}
4. If x ∈ I, then the solution set of the inequation 1 < 3x + 5
≤
11 is
(a) {- 1, 0, 1, 2}
(b) {- 2, - 1, 0, 1}
(c) {- 1, 0, 1}
(d) {x : x ∈ R, - (4/3) < x
≤
2}
Answer
(a) {- 1, 0, 1, 2}
x ∈ I
1 < 3x + 5 ≤ 11
⇒ 1 < 3x + 5
⇒ 1 - 5 < 3x
⇒ - 4 < 3x
⇒ -4/3 < x
And 3x + 5 ≤ 11 ⇒ 3x ≤ 11 - 5
⇒ 3x ≤ 6
⇒ x ≤ 6/3
⇒ x ≤ 2
∴ -4/3 < x ≤ 2
Solution set = {- 1, 0, 1, 2}
5. If x ∈ R, the solution set of 6
≤
- 3(2x - 4) < 12 is
(a) { x : x ∈ r, 0 < x
≤
1}
(b) { x : x ∈ R, 0
≤
x < 1}
(c) {0, 1}
(d) none of these
Answer
(a) {x : x ∈ R, 0 < x ≤ 1}
x ∈ R
⇒ 6 ≤ - 3(2x - 4) < 12
⇒ 6 ≤ - 3(2x - 4)
⇒ 6 ≤ - 6x + 12
⇒ 6x ≤ 12 - 6
⇒ 6x ≤ 6
⇒ x ≤ 6/6
⇒ x ≤ 1
And -3(2x - 4) < 12
⇒ - 6x + 12 < 12
⇒ - 6x < 0
⇒ x < 0 .........(ii)
From (i) and (iii),
∴ 0 < x ≤ 1
Solution set = {x : x ∈ R, 0 < x ≤ 1}
Chapter Test
1. Solve the inequation : 5x - 2 ≤ 3(3 - x) where x
∈ {- 2, - 1, 0, 1, 2, 3, 4} . Also represent its solution on the number line.
Answer
5x - 2 < 3(3 - x)
⇒ 5x - 2 ≤ 9 - 3x
⇒ 5x + 3x ⇒ 9 + 2
⇒ 8x ≤ 11
⇒ x ≤ 11/8
∵ x ∈ {-2, - 1, 0, 1, 2, 3, 4}
∴ Solution set = {- 2, - 1, 0, 1}
Solution set on number line

2. Solve the inequations:
6x - 5 < 3x + 4, x ∈ I.
Answer
6x - 5 < 3x + 4
⇒ 6x - 3x < 4 + 5
⇒ 3x < 9
⇒ x < 3
x ∈ I
Solution set = {-1, - 2, 2, 1, 0.........}
3. Find the solution set of the inequation x + 5 < 2x +3 ; x ∈ R
Graph the solution set on the number line.
Answer
x + 5 ≤ 2x + 3
⇒ x - 2x ≤ 3 - 5
⇒ - x ≤ - 2
⇒ x ≥ 2
∵ x ∈ R
∴ Solution set = {2, 3, 4, 5, .......}
Solution set on number line

4. If x ∈ R (real numbers) and - 1 < 3 - 2x
≤
7, find the solution set and represent it on a number line.
Answer
- 1 < 3 - 2x ≤ 7
⇒ -1 < 3 - 2x and 3 - 2x ≤ 7
⇒ 2x < 3 + 1 and - 2x ≤ 7 - 3
⇒ 2x < 4 and - 2x ≤ 4
⇒ x < 2 and - x ≤ 2
And x ≥ - 2 or - 2 ≤ x
x ∈ R
Solution set - 2 ≤ x < 2
Solution set on number line
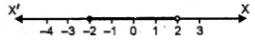
5. Solve the inequation:
(5x + 1)/7 - 4(x/7 + 2/5)
≤
1.3/5 + (3x - 1)/7, x ∈ R
Answer
(5x + 1)/7 - 4(x/7 + 2/5) ≤ 1.3/5 + (3x - 1)/7
(5x + 1)/7 - 4(x/7 + 2/5) ≤ 8/5 + (3x - 1)/7
Multiplying by L.C.M. of 7 and 5 i.e., 35
25x + 5 - 4 (5x + 14) ≤ 56 + 15x - 5
⇒ 25 + 5 - 20x - 56 ≤ 56 + 15x - 5
⇒ 25x - 20x - 15x ≤ 56 - 5 - 5 + 56
⇒ - 10x ≤ 102
⇒ - x ≤ 102/10
⇒ - x ≤ 51/5
⇒ x ≥ - 51/5
∵ x ∈ R
∴ Solution set = {x : x ∈ R, x ≥ - 51/5}
Question 6: Find the range of values of a, which satisfy 7
≤
- 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.
Solution:
7 < - 4x + 2 < 12
⇒ 7 < - 4x + 2 and - 4x + 2 < 12
⇒ 4x ≤ 2 - 7 and - 4x < 12 - 2
⇒ 4x ≤ - 5 and - 4x < 10
⇒ x ≤ -5/4 and - x < 10/4
⇒ x ≤ -5/4 and - x < 5/2
or x > - (5/2)
∵ x ∈ R
∴ Solution set - 5/2 < x ≤ -5/4
= {x : x ∈ R, - 5/2 < x ≤ - 5/4}
Solution set on the number line

7. If x ∈ R, solve 2x - 3
≥
x + (1 - x)/3 > 2/5x
Answer
2x - 3 ≥ x + (1 - x)/3 > 2/5.x
⇒ 2x - 3 ≥ x + (1 - x)/3 and x + (1 - x)/3 > 2/5x
⇒ 2x - 3 ≥ (3x + 1 - x)/3 and (3x + 1 - x)/3 > 2/5x
⇒ 6x - 9 ≥ 3x + 1 - x and 15x + 5 - 5x > 6x
⇒ 6x - 3x + x ≥ 1 + 9 and 15x - 6x - 5x > - 5
⇒ 4x ≥ 10 and 4x > - 5
⇒ x ≥ 10/4 and x > - 5/4
⇒ x ≥ 5/2
∴ x ≥ 5/2
∵ x ∈ R
∴ Solution set = {x : x ∈ R, x ≥ 5/2}
Solution set on number line

8. Find positive integers which are such that if 6 is subtracted from five times the integer then the resulting number cannot be greater than four times the integer.
Answer
Let the positive integer = x
According to the problem,
5a - 6 - 4x
⇒ 5a - 4x < 6
⇒ x < 6
Solution set = {x : x < 6}
= {, 2, 3, 4, 5, 6}
9. Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is at least 3.
Answer
Let first least natural number = x
Then second number = x + 1
And third number = x + 2
According to the condition 1/3(x + 2) - 1/5 (x) ≥ 3
5x + 10 - 3x ≥ 45
(Multiplying by 15 the L.C.M. of 2 and 5)
2x ≥ 45 - 10
⇒ 2x ≥ 35
x ≥ 35/2
⇒ x ≥ 17.1/2
∵ x is a natural least number
∴ x = 18
∴ find least natural number = 18
Second number = 18 + 1 = 19
And third numbers = 18 + 2 = 20
Hence, least natural numbers are 18, 19, 20