Previous Year Paper year:2011 : ICSE-X-Mathematics

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2011

with Solutions - page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#3-a-ii
The rate of interest

#3-b [3]
Calculate the area of the shaded region, if the diameter of the semi circle is equal
to 14 cm.
Take (``\pi = \frac{22}{7}``)
.

Ans : Area of shaded portion = Total area . area of the two quadrants
``= (Area \ of \ ACDE + \ Area \ of \ semi \ circle \ EFD) - \\ (Area \ of \ Quadrant \ ABE + Area \ of \ Quadrant \ BCD) ``
``= (14 \times 7 + \frac{1}{2} \pi \times 7^2) - (\frac{1}{4} \times \pi \times 7^2 + \frac{1}{4} \times \pi \times 7^2 )``
``= 98 \ cm^2 ``

#3-c [4]
ABC is a triangle and G(4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b)
and C = (a, 1), find .a. and .b.. Find length of side BC.
Ans : Since G is the centroid
4`` = \frac{1+4+a}{3} \Rightarrow a=7 ``
``3= \frac{3+b+1}{3} \Rightarrow b = 5``
Therefore ``B(4, 5) \ and \ C(7, 1)``
Therefore ``BC=\sqrt{(7-4)^2+(1-5)^2} = \sqrt{25} = 5`` units.

#4

#4-a [3]
Solve the following inequation and represent the solution set on the number line
$$2x . 5 \le 5x + 4 < 11, \text{where x } \epsilon I $$
Ans : ``2x-5 \leq 5x+4 < 11``
``2x-5 \leq 5x+4 or -9 \leq 3x or -3 \leq x ``
``5x+4 < 11 or 5x < 7 or x < \frac{7}{5}``
``-3 \leq x <\frac{7}{5} ``
Therefore ``x \in \{-3, -2, -1, 0, 1 \}``

#4-b [3]
Evaluate without using trigonometric tables. [4]
$$ 2(\frac{\tan 35°}{\cot 55°})^2 + \frac{\cot 55°}{\tan 35°} -3 \frac{\sec 40 °}{cosec 50 °} $$
Ans : ``2 (\frac{tan \ 35°}{cot \ 55°})^2 + (\frac{cot \ 55°}{tan \ 35°})^2 - 3 (\frac{sec \ 40°}{cosec \ 50°}) ``
``= 2 (\frac{tan \ 35°}{cot \ (90° - 35°)})^2 + (\frac{cot \ 55°}{tan \ (90° - 55°)})^2 - 3 (\frac{sec \ 40°}{cosec \ (90° - 40°)}) ``
``= 2 (\frac{tan \ 35°}{tan \ 35°})^2 + (\frac{cot \ 55°}{cot \ 55°})^2 - 3 (\frac{sec \ 40°}{sec \ 40°}) ``
= 2 + 1 - 3 = 0

#4-c [4]
A Mathematics aptitude test of 50 students was recorded as follows:

Marks 50 - 60 60 - 70 70 - 80 80 - 90 90 . 100
No. of Students 4 8 14 19 5

Draw a histogram from the above data using a graph paper and locate the mode.
Ans :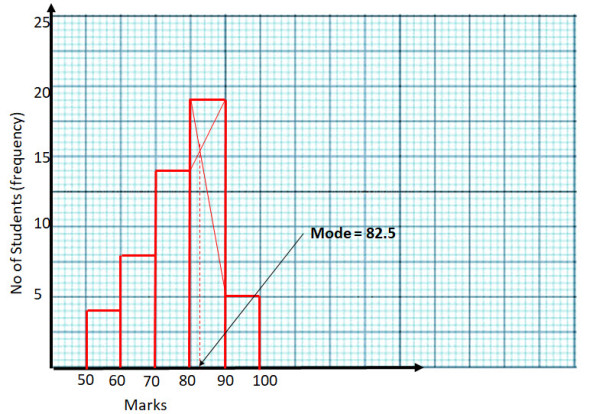

# [40]
Section : B
Attempt any four questions from this section

#5

#5-a [3]
A manufacturer sells a washing machine to a wholesaler for Rs. 15000. The
wholesaler sells it to a trader at a profit of Rs. 1200 and the trader in turns sells it
to a consumer at a profit of Rs. 1800. If the rate of VAT is 8% find:
Ans : (i) Tax received by the manufacturer ``= \frac{8}{100} \times 1500 = Rs. 1200``
For the trader the price ``= 15000+1200= Rs. \ 16200``
Tax paid by the trader ``= \frac{8}{100} \times 16200 = Rs. \ 1296 ``
Therefore VAT received from wholesaler ``= 1296-1200 = Rs. \ 96``
Price for the consumer ``= 16200+1800 = Rs. \ 18000 ``

#5-a-i
The amount of VAT received by the state government on the sale of this
machine from the manufacturer and the wholesaler.

#5-a-ii
The amount that the consumer pays for the machine.
Ans : Tax paid by the consumer ``= \frac{8}{100} \times 18000 = Rs. \ 1440 ``
Hence the total price paid by the consumer ``= 18000+1440 = Rs. \ 19440 ``

#5-b [3]
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres
of radius 0.5 cm. Find the number of spheres formed.
Ans : Cone: Radius : ``5 \ cm`` and Height ``8 \ cm``
Sphere: ``0.5 \ cm ``
Number of sphere ``= \frac{Volume \ of \ the \ cone}{Volume \ of \ the \ small sphere}``
`` = \frac{\frac{1}{3} \pi (5)^2 \times 8}{\frac{4}{3} \pi (0.5)^2}``
``= \frac{25 \times 8}{4 \times 0.125} = 400``

#5-c [4]
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find
Ans : (i) Mid point of ``BD = (\frac{5+2}{2}, \frac{-4+8}{2})= (\frac{7}{2}, 2)``
Therefore we have ``A(x, y), O(\frac{7}{2}, 2) \ and \ C(4, 7)``
O is the mid point of AC as well (diagonals of a parallelogram bisect each other)
Hence ``\frac{x+4}{2} = \frac{7}{2} \Rightarrow x = 3 ``
and ``\frac{y+7}{2} = 2 \Rightarrow y = -3 ``
Hence A ( 3, -3)

#5-c-i
Coordinates of A